Так как задача математической логики состоит в описании общих методов умозаключений, то алгебра предикатов должна строиться так, чтобы среди ее символов не было символов, принадлежащих конкретным моделям или классам моделей. Вместо символов предикатов фиксированной сигнатуры в алгебре предикатов используются символы предикатных переменных. Из алгебры предикатов замещением предикатных переменных предикатами сигнатуры z выделяется алгебра предикатов сигнатуры z.
Введем счетное множество предикатных переменных 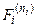 ,
, 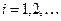 , счетное множество символов предметных переменных, символы операций и круглые скобки.
, счетное множество символов предметных переменных, символы операций и круглые скобки.
Понятие формулы алгебры предикатов определяется также как и формулы алгебры предикатов сигнатуры z. Число всех символов операций, входящих в запись формулы U, называется её рангом и обозначается 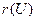 . Формула
. Формула 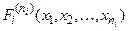 называется атомарной, она может записываться
называется атомарной, она может записываться 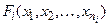 , её ранг = 0.
, её ранг = 0.
Формула алгебры предикатов сигнатуры s является или высказыванием или некоторым предикатом на модели M. Формула алгебры предикатов является только определенным образом построенной последовательностью символов. Из одной и той же формулы алгебры предикатов можно образовать различные формулы сигнатуры z и формулы различных сигнатур, после чего можно будет говорить об истинностных значениях формулы алгебры предикатов.
Определение. Пусть U - формула алгебры предикатов и
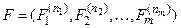 (2)
(2)
набор предикатных переменных, входящих в U. Сигнатуру z, а также класс моделей Kz и модель M Î Kz назовем допустимыми для формулы U, если z содержит хотя бы один предикат арности ni для любого  , т.е. существует отображение
, т.е. существует отображение 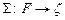 .
.
Такое отображение назовем сигнатурным. Формула, полученная заменой каждой предикатной переменной 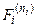 её образом S(
её образом S(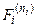 ), является формулой сигнатуры z и обозначается s U.
), является формулой сигнатуры z и обозначается s U.
Например, для формулы алгебры предикатов
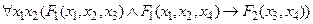
модель арифметики натуральных чисел N = < N; E, S, P > является допустимой, так как можно построить сигнатурное отображение 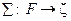 множества предикатных переменных формулы
множества предикатных переменных формулы 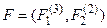 в сигнатуру модели z = < E (2), S (3), P (3)>. Вариантов такого отображения два:
в сигнатуру модели z = < E (2), S (3), P (3)>. Вариантов такого отображения два:
1) 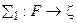 ,
, 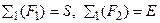 ;
;
2) 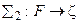 ,
,  .
.
Обозначим через s U формулу, полученную подстановкой в формулу U предикатов сигнатурного отображения å.
Определение. Пусть для формулы алгебры предикатов U модель M является допустимой. Тогда:
a) формула U называется выполнимой на модели M, если формула s U выполнима на модели M при некотором сигнатурном отображении S;
b) формула U называется выполнимой, если существует допустимая модель, на которой она выполнима;
c) формула U называется невыполнимой или ложной на модели M, если формула s U невыполнима на модели M при любом сигнатурном отображении S;
d) формула U называется невыполнимой, если на любой допустимой модели она не выполнима;
e) формула U называется тождественно истинной на модели M, если формула s U истинна на модели M при любом сигнатурном отображении S;
f) формула U называется общезначимой, если она тождественно истинна на любой допустимой модели.
Примеры.
Формула алгебры предикатов 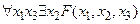 на допустимой модели арифметики натуральных чисел N = < N; E, S, P > является ложной, так как для любых
на допустимой модели арифметики натуральных чисел N = < N; E, S, P > является ложной, так как для любых 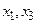 не существует такое натуральное x 2, что
не существует такое натуральное x 2, что 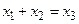 или
или 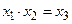 .
.
Формула алгебры предикатов  общезначима.
общезначима.
Основные общезначимости алгебры предикатов
1. 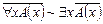
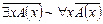
2. 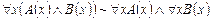

3. 

4. 


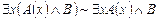
5. 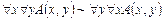
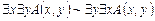
Докажем формулу  .
.
Так как единственная переменная в обеих частях эквиваленции связана, то обе они являются высказываниями. Поэтому для доказательства общезначимости формулы, покажем, что истинностные значения левой и правой части совпадают для любых одноместных предикатов  , определённых на произвольном множестве M.
, определённых на произвольном множестве M.
Пусть  , тогда по определению операции утверждения существования
, тогда по определению операции утверждения существования 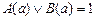 для некоторого a из M. Следовательно,
для некоторого a из M. Следовательно,  , где
, где 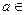 M. Воспользовавшись снова определением операции утверждения существования, получим, что
M. Воспользовавшись снова определением операции утверждения существования, получим, что 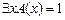 или
или 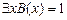 , а, следовательно, истинна и их дизъюнкция
, а, следовательно, истинна и их дизъюнкция  .
.
Пусть теперь  , тогда
, тогда 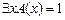 или
или 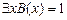 . В первом случае получим, что
. В первом случае получим, что 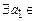 M,
M, 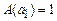 , во втором –
, во втором – 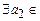 M,
M, 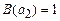 . Однако в обоих случаях существует такой элемент
. Однако в обоих случаях существует такой элемент  M, что
M, что 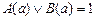 , в первом случае
, в первом случае  , во втором –
, во втором – 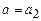 . А это означает, что
. А это означает, что  .
.
На множестве формул алгебры предикатов можно ввести отношение эквиваленции.
Определение. Формула алгебры предикатов U называется эквивалентной формуле V (обозначается U º V), если их эквиваленция общезначима.
Множество формул алгебры предикатов можно разбить на классы эквивалентности, включив в один класс эквивалентные между собой формулы. Каждой формуле U соответствует класс эквивалентности, который обозначается [ U ].
Определение. Формула алгебры предикатов называется приведенной, если она содержит операции утверждения всеобщности, существования, конъюнкции, дизъюнкции и операцию отрицания, относящуюся к атомарным формулам.
Теорема 3.1. Каждый класс эквивалентности [ U ] может быть представлен приведенной формулой, т.е. для любой формулы U существует эквивалентная ей приведенная формула V.
Для формул алгебры предикатов существуют предваренные нормальные формы.
Определение. Предваренной нормальной формой (ПНФ) формулы алгебры предикатов называется формула, имеющая вид
 ,
,
где 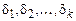 – некоторые кванторы, а U – бескванторная приведенная формула. Выражение
– некоторые кванторы, а U – бескванторная приведенная формула. Выражение  называется префиксом, а U – матрицей нормальной формы.
называется префиксом, а U – матрицей нормальной формы.
Будем говорить, что бескванторная формула U находится в ДНФ (КНФ), если U получается из формулы алгебры высказываний, находящейся в ДНФ (КНФ), подстановкой вместо пропозициональных переменных некоторых атомарных формул.
ПНФ называется пренексной нормальной формой (ПННФ), если её матрица имеет вид ДНФ, и предклазуальной (пкнф), если – КНФ.
Построим ПН-форму для формулы
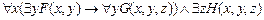 .
.
Преобразуем формулу к приведенному виду
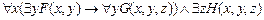 º
º
º  º
º
º  .
.
Так как для квантора " и операции Ú нет соответствующей эквивалентности, то переименуем связанную переменную y второго операнда дизъюнкции и вынесем кванторы по переменным, от которых не зависит другой операнд вперёд
 º
º
º 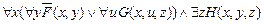 º
º
º 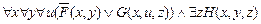 .
.
В первом операнде конъюнкции последней формулы переменные x и y – связанные, а z – свободная, а во втором – наоборот. Переобозначив снова связанные переменные, получим
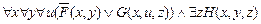 º
º
º 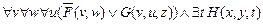 º
º
º 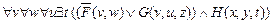 .
.
Полученная предваренная нормальная форма является предклазуальной.
Использование формул алгебры предикатов в информационных технологиях породило необходимость преобразования формул в бескванторные, так как работать с такими формулами значительно легче, чем с формулами, содержащими кванторы. Основой такого преобразования являются аксиомы Сколема:
1) 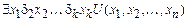 Þ
Þ 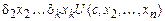 ;
;
2) 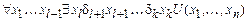 Þ
Þ  .
.
Возможность удаления кванторов всеобщности непосредственно следует из определения операции, так как 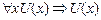 для произвольного x.
для произвольного x.
Формула U находится в клазуальной нормальной форме, если она получена из формулы, находящейся в предклазуальной нормальной форме, удалением кванторов существования в соответствии с аксиомами Сколема и последующим удалением всех кванторов всеобщности. Процесс такого преобразования называется сколемизацией.
Так клазуальная нормальная форма для формулы предыдущего примера имеет вид
 .
.