Определим эквивалентность формул в исчислении высказываний.
Определение 1. Формулы U и B называются эквивалентными, что обозначается |-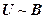 
, если
|- 
(1)
Рассмотрим некоторые простые свойства отношения эквивалентности.
1. Рефлексивность: |- 
.
2. Симметричность: если |- 
, то |- 
.
3. Транзитивность: если |- и |- 
, то |-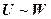 
.
Задание 1. Доказать свойство симметричности отношения эквивалентности.
Решение.
1. |- 
2. |- 
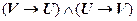
3. |-
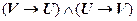
Из свойств отношения эквивалентности следует, что множество формул исчисления высказываний разбивается на непересекающиеся классы эквивалентных друг другу формул (классы эквивалентности). Следовательно, все теоремы исчисления высказываний образуют один класс эквивалентных формул.
В исчислении высказываний имеют место следующие эквивалентности, которые соответствуют аналогичным свойствам отношения эквивалентности алгебры высказываний.
1. |- 
.
2. |- 
3. |- 
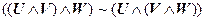
4. |- 
5. |- 
6. |- 
7. |- 
8. |- 
9. |- 
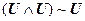
10. |- 
11. |- 
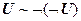
12. |- 
Для того чтобы доказать эквивалентность |- 
в исчислении высказываний достаточно построить выводы 
|- 
и |- . Покажем, что если |- и |- , то |- .
| 1. |-
| по условию |
| 2. |-
| по условию |
3. |- 
| 5 (1) |
4. |- 
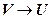
| 5 (2) |
| 5. , |-
| |
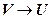6. |- 
| 4 (3, 4, 5) |
Последняя формула, в силу определения, означает ú- 
.
Теорема эквивалентности. Есл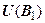и 
и 
- формулы, полученные заменой некоторых (одних и тех же) вхождений какой-либо высказывательной переменной в формуле U соответственно формулами 
и 
, то
|- 
.
Следствие. Если есть некоторая подформула формулы U и эквивалентна формуле , то формула, полученная заменой в формуле U на , эквивалентна U. Иными словами, если , то .
Свойства 2, 4, 10 и теорема эквивалентности позволяют формулу, составленную из высказывательных переменных 
лишь с помощью операции дизъюнкции, преобразовать к виду
.
Аналогично формула, составленная из 
с помощью операции конъюнкции эквивалентна формуле
.
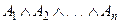Это позволяет дать определение понятиям нормальных форм исчисления высказываний, которые совпадают с соответствующими определениями алгебры высказываний.
Теорема 3.1. Для каждой формулы исчисления высказываний существуют эквивалентные ей дизъюнктивная и конъюнктивная нормальные формы.
Исчисление секвенций ИС
Исчисление высказываний генценовского типа называется исчислением секвенций ИС.
Алфавит ИС состоит из символов алфавита ИВ, дополненных символом |-. Допустимые последовательности символов – формулы определяются также как и в ИВ, кроме того, в ИС вводится понятие секвенция.
Пусть U1, U2,..., Un, V – формулы ИС. Секвенциями называются конечные последовательности следующих двух видов:
1) U1, U2,..., Un |- V (из истинности U1, U2,..., Un следует истинность V);
2) U1, U2,..., Un |- (система формул U1, U2,..., Un противоречива).
Множество аксиом ИС определяется единственной схемой секвенций U |- U. Правила вывода ИС определяются следующими записями, где T, T 1 – конечное множество формул (возможно пустое).
1. 
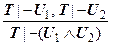(введение Ù).
2. 
(удаление Ù).
3. 
(удаление Ù).
4. 
(введение Ú).
5. 
(введение Ú).
6. 
(удаление Ú или правило разбора двух случаев).
7. 
(введение ®).
8. 
(удаление ®).
9. 
(удаление Ø или доказательство от противного).
10. 
(выведение противоречия).
11. 
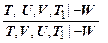(перестановка посылок).
12. 
(уточнение или правило лишней посылки).
Исчисления ИВ и ИС эквивалентны.