Определим исчисление предикатов гильбертовского типа ИП. Это исчисление является расширением исчисления высказываний ИВ.
В алфавит ИВ добавим строчные латинские буквы для обозначения предметных переменных и символы кванторов " и $. Язык исчисления составляют формулы, определяемые также, как в алгебре предикатов.
Аксиоматика исчисления дополняется двумя схемами аксиом:
11. 
12. 
,
где 
- произвольная формула, содержащая свободные вхождения переменной x, причем ни одно из них не находится в области действия квантора по переменной y, а 
получена из заменой свободных вхождений x на y.
К правилу заключения ИВ добавляются два правила, связанные с кванторами. Пусть 
и 
– формулы, которые содержат и не содержат свободные вхождения переменной x соответственно.
2. Правило обобщения (введения ")
.
3. Правило введения $
.
Правила естественного вывода дополняются 4-мя правилами. Пусть
14. Правило введения квантора ".
Если T |- U (x), то T |- " x U (x).
15. Правило удаления квантора ".
Если T |- " x U (x), то T |- U (y).
16. Правило введения квантора $.
Если T |- U (y), то T |- $ x U (x).
17. Правило удаления квантора $.
Если T, U (x) |- V, то T, $ x U (x) |- V.
Рассмотрим пример вывода в ИП.
Доказать, что в ИП 
|- 
| 1. |-
| |
2. |- 
| 15 (1) |
3. |- 
| 14 (2) |
Исчисление предикатов генценовского типа ИПС строится расширением исчисления ИП.
Прикладные исчисления предикатов
Прикладные исчисления предикатов строятся добавлением к исчислению предикатов своих собственных аксиом. Причем, в прикладных исчислениях предикатов вводится понятие терма. Термами являются:
1) предметные переменные и константы;
2) предметные функции.
В аксиомах прикладных исчислений предикатов наряду с предметными переменными могут использоваться произвольные термы, так аксиомы 11, 12 в них имеют вид:
11') 
12') 
,
где t – произвольный терм.
Всюду далее будут рассматриваться прикладные исчисления предикатов первого порядка, т. е. исчисления, в которых кванторами связываются только предметные переменные, а не предикаты и функции.
Исчисление с равенством.
В данном исчислении вводится предикат =, а к аксиомам ИП добавляются аксиомы равенства.
E1. 
E2. 
Здесь Е1 является аксиомой, а Е2 – схемой аксиомы, где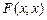 
– произвольная формула, а 
– формула, полученная из 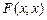заменой некоторых вхождений x на y.
Теорема 6.1. В любой теории с равенством:
1) |- 
для любого терма t;
2) |- 
;
3) |- 
.
Доказательство. 1) Данное утверждение непосредственно следует из аксиом 11’ и Е1, где 
.
Для свойств 2), 3) построим формальные выводы формул.
2)
1. |- 
| Е2 
|
2.  |- 
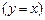
| 6 (1) |
| 3. |-
| Е1 |
4.  |-
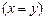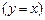
| 3 (2, 3) |
| 5. |-
| 5 (4) |
3)
1. |- 
| Е2 |
2. |- 
| 1, где  , 
|
3. |- 
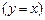| 6 (2) |
| 4. |-
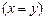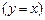
| Теорема исчисления с равенством |
| 5. |-
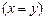| 4 (4, 3) |
| 6. |-
| 5 (5) |
Строгий частичный порядок.
Предикатом строгого частичного порядка является предикат <, а дополнительными – следующие аксиомы.
NE1. 
NE2. 
Формальная арифметика.
Формальная арифметика определяется как исчисление с равенством на предметном множестве ô, в котором вводятся предметная константа 0 и предметные функции +, ×, ¢, задаваемые аксиомами.
A1. 
A2. 
A3. 
A4. 
A5. 
A6. 
A7. 
A8. 
Здесь А1-А7 – аксиомы, а А8 – схема аксиомы, определяющая доказательство по индукции.