Замена переменных в двойном интеграле
Рассмотрим двойной интеграл  в декартовых координатах
в декартовых координатах  . Пусть имеются две гладкие функции двух переменных
. Пусть имеются две гладкие функции двух переменных  ,
,  , то есть эти функции непрерывны вместе со своими частными производными первого порядка по переменным
, то есть эти функции непрерывны вместе со своими частными производными первого порядка по переменным  и
и  в некоторой замкнутой области
в некоторой замкнутой области 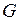 плоскости
плоскости  . И пусть эти функции взаимно однозначно и непрерывно отображают область
. И пусть эти функции взаимно однозначно и непрерывно отображают область  на область
на область 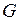 . Тогда имеет место равенство
. Тогда имеет место равенство
 ,
,
если  , где
, где 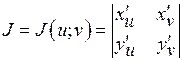 – якобиан преобразования
– якобиан преобразования  в
в 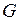 . Определитель
. Определитель  назван в честь немецкого математика Якоби. Геометрически
назван в честь немецкого математика Якоби. Геометрически  выражает элемент площади в области
выражает элемент площади в области 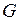 , а
, а  – коэффициент изменения элемента площади в области
– коэффициент изменения элемента площади в области  при преобразовании в элемент площади в области
при преобразовании в элемент площади в области 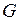 .
.
Координаты  называются криволинейными координатами точки
называются криволинейными координатами точки  .
.
Интеграл  называется двойным интегралом в криволинейных координатах.
называется двойным интегралом в криволинейных координатах.
Частным случаем криволинейных координат являются полярные координаты  .
.
Двойной интеграл в полярных координатах
Полярные координаты связаны с прямоугольными формулами  ,
,  (
( ,
, 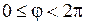 ). Якобиан преобразования в этом случае равен
). Якобиан преобразования в этом случае равен
 ,
,
а  – элемент площади в полярных координатах.
– элемент площади в полярных координатах.
Формула перехода от декартовых координат к полярным координатам
 .
.
Если областью является круг или часть круга, то в двойном интеграле удобно перейти к полярным координатам, так как уравнение окружности 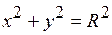 в полярных координатах приобретает простой вид
в полярных координатах приобретает простой вид  .
.
Расстановка пределов в полярных координатах выполняется аналогично случаю декартовых координат.
Пример 1. Вычислить двойной интеграл  , где область
, где область
 :
:  ,
,  ,
,  .
.
Решение. Построим область  . Так как областью является четверть круга (рис. 1), перейдём к полярным координатам по формулам
. Так как областью является четверть круга (рис. 1), перейдём к полярным координатам по формулам  ,
,  ,
,  . Точкой входа является полюс
. Точкой входа является полюс  (рис. 2), а линией выхода – окружность
(рис. 2), а линией выхода – окружность  . Область
. Область  определяется системой неравенств
определяется системой неравенств 

Подынтегральная функция в полярных координатах  .
.
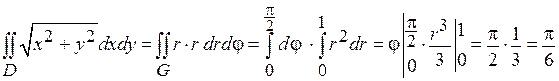 .
.
Замечание. Повторный интеграл в примере 1 свёлся к произведению двух независимых друг от друга определённых интегралов, поскольку результат вычисления внутреннего интеграла есть число.
Пример 2. Перейти в двойном интеграле  к полярным координатам и расставить пределы интегрирования, если область
к полярным координатам и расставить пределы интегрирования, если область  ограничена линиями: а)
ограничена линиями: а)  ,
,  ,
,  (
( ),
),  (
(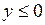 );
);
б)  ,
,  ,
,  .
.
Решение 2а). Областью является четверть кольца в четвёртой четверти координатной плоскости ( ,
, 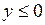 ), между окружностями с радиусами
), между окружностями с радиусами  и
и  (рис. 3). В полярной системе координат область
(рис. 3). В полярной системе координат область 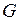 определяется системой
определяется системой 
 .
.
 Решение 4б). Уравнение окружности с центром в точке
Решение 4б). Уравнение окружности с центром в точке  имеет вид:
имеет вид:  . Приведём к такому виду уравнение
. Приведём к такому виду уравнение  . Перенесём
. Перенесём  влево и выделим полный квадрат
влево и выделим полный квадрат
 .
.
Получим уравнение окружности с центром в точке  и радиусом
и радиусом  (рис. 4). В полярной системе координат уравнение окружности имеет вид
(рис. 4). В полярной системе координат уравнение окружности имеет вид  . Уравнение прямой
. Уравнение прямой  представим к виду
представим к виду  , а так как тангенс угла наклона прямой к оси абсцисс
, а так как тангенс угла наклона прямой к оси абсцисс  , то
, то  . Прямая
. Прямая  наклонена к оси
наклонена к оси  под углом
под углом  . Область
. Область 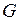 определяется системой неравенств
определяется системой неравенств 
 .
.
Пример 3. Найти массу пластинки, имеющую форму четверти круга радиуса  , если известно, что поверхностная плотность в каждой точке пластинки пропорциональна расстоянию до этой точки от центра круга.
, если известно, что поверхностная плотность в каждой точке пластинки пропорциональна расстоянию до этой точки от центра круга.
Решение. Область  (рис. 5) в декартовой системе координат определяется неравенствами
(рис. 5) в декартовой системе координат определяется неравенствами  . Поверхностная плотность в любой точки области определяется уравнением
. Поверхностная плотность в любой точки области определяется уравнением  (рис. 6).
(рис. 6).
|

Перейдём к полярным координатам
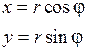
| 
| 
|
 .
.
Пример 4. В условиях задачи 3 найти координаты центра масс точки  .
.
Решение. Статический момент относительно оси 


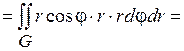

 .
.
Координата  точки
точки  :
:  .
.
Статический момент относительно оси 




 .
.
Координата  точки
точки  :
:  .
.
Ответ:  .
.
Тройной интеграл


| Пусть в области 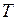 пространства задана функция пространства задана функция  .
Выполним следующие построения:
1) разделим область .
Выполним следующие построения:
1) разделим область 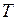 на части плоскостями параллельными координатным плоскостям на части плоскостями параллельными координатным плоскостям  (объёмы частей); (объёмы частей);
|
2) диаметры частей обозначим 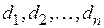 , а
, а  ;
;
3) в каждой части выберем произвольно по точке  ;
;
4) составим сумму (интегральную)

Определение. Предел интегральной суммы (4) при  называется тройным интегралом по области
называется тройным интегралом по области 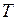 от функции
от функции  и обозначается
и обозначается
 или
или  .
.

| По определению   . .
 элемент объёма. элемент объёма.
|
 Физический смысл можно интерпретировать как массу неоднородного тела с объёмной плотностью
Физический смысл можно интерпретировать как массу неоднородного тела с объёмной плотностью 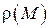 .
.
 – элемент массы,
– элемент массы,  – суммарная масса.
– суммарная масса.
 Основные свойства.
Основные свойства.
1º. Свойства линейности.  ,
,
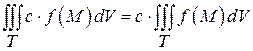 .
.

| 2º. Свойство аддитивности.

|
3º. Оценка тройного интеграла.
 в области
в области 
 .
.
 Правило вычисления.
Правило вычисления.