Тема: Натуральный минор во фригийских оборотах

Гармония

Г. Группа МИД-18, МИВ-18

Г. Группа МИИ-18

Тема: Натуральный минор во фригийских оборотах

1.Функциональная система.
Полная функциональная система натурального минора восновном отличается от системы гармонического минора строением доминантовой группы — d, dtlll, dVII. В ней главное трезвучие — минорное, побочные же трезвучия — мажорные. Все аккорды группы на основании строения главного трезвучия обозначаются, как известно, малыми буквами:

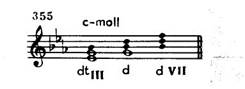
Отсутствие повышенной VII ступени ослабляет остроту тяготения этих аккордов к тонике, и потому их применение связано с особыми условиям
2.Фригийский оборот и логика последовательностей
Натуральный минор вообще вводится эпизодически и на небольших участках произведения. Главной основой для его введения служит поступенное движение одного из голосов от основного звука тоники вниз к V ступени:

Образующийся таким путем нисходящий верхний тетрахорд натуральной минорной гаммы совпадает по своему интервальному строению с тетрахордом старинного фригийского лада (б. 2 — б. 2 — м. 2 в нисходящем порядке). В связи с этим гармонизованный мелодический ход голоса по звукам нисходящего верхнего тетрахорда натуральной минорной гаммы называется фригийским оборотом. Если он служит заключением построения, заканчивающегося на основном трезвучии D, то его называют фригийской каденцией.
Как известно, VII ступень гаммы — признак доминантовой группы, VI ступень —признак субдоминанты. Поэтому фригийский тетрахорд, состоящий из I—VII—VI—V ступеней, вызывает естественную последовательность доминантовой, а затем субдоминантовой гармонии. Типичная формула последовательностей, связанных с фригийским оборотом, таким образом, противоположна основной формуле мажора и гармонического минора:

По старинной традиции фригийский оборот доводится, как правило, до доминанты, которая обычно принадлежит уже гармоническому, а не натуральному минору. Это объясняет эпизодическую роль натурального минора, ибо за гармонической D восстанавливается общий тип последовательностей, свойственный гармоническому минору.
фригийский оборот в гармонический минор D D, l₍ s K⁶4 D t
(ряд последований) натур, миноре
t—d—s. Следовательно, до фригийского оборота и после него движение аккордов идет в гармоническом миноре.
Примечание. Как уже указывалось, в последовательности аккордов мажора и минора, отвечающих формуле Т—S—4)—Т, напряжение при переходе от S к D увеличивается. В натуральном миноре формула t—d—s—t также нередко создает повышение напряжения от d к s, ибо в натуральной доминанте (благодаря отсутствию полутонового восходящего тяготения) неустойчивость смягчена, и потому следующая за ней субдоминанта воспринимается как более напряженное созвучие, так как терция субдоминанты более явно тяготеет к квинте тонического трезвучия (полутон).
Возможны обороты, подобные фригийскому, и при отсутствии начального звука или при отдалении заключительного:

c-moll

3.Фригийский тетрахорд в верхнем голосе
Когда фригийский тетрахорд проводится в верхнем голосе, он гармонизуется чаще всего следующим образом:
1)t—dtlll—s—D
tsVI—dtIII_e—s—D:

2) Употребительна последовательность параллельных секстаккордов U—dVII₆—tsVI₆—D₆ (или D⁶₅, DVII₇, или SII₂—D₆), с попеременно различными удвоениями:

3) VII натуральная ступень гаммы может также рассматриваться как септима тоники, в частности — проходящая:

4.Фригийский тетрахорд в басу.