Вопросы и задачи для самостоятельной работы
1. Являются ли векторами направленные отрезки, для которых произведение на число определяется стандартным образом, а суммой считается отрезок суммарной длины, направленный вдоль биссектрисы угла, образованного слагаемыми?
- Материальная точка движется так, что ее декартовы координаты изменяются во времени по закону:
a. 
Записать зависимости от времени сферических и цилиндрических координат точки, нарисовать примерный вид траектории материальной точки.
- Найти зависимость от времени декартовых, цилиндрических и сферических координат материальной точки, равномерно вращающейся с периодом Т по окружности большого круга сферы радиуса R, проходящей через полюса этой сферы.
- Частица равномерно движется по винтовой линии, «навитой» на поверхность цилиндра радиуса R, делая один оборот вокруг оси за время T и смещаясь вдоль оси цилиндра с постоянной скоростью v. Найти зависимости от времени декартовых, цилиндрических и сферических координат тоски. Ориентацию в пространстве систем координат выберите так, как сочтете более удобным.
- *) Попытайтесь заставить Ваш компьютер изобразить на экране декартову систему координат, оси которой весьма желательно иметь возможность вращать при помощи «мыши» или клавиш компьютера. Научите Ваш компьютер отображать точку в этой системе координат по задаваемым пользователем ее декартовым, сферическим или цилиндрическим координатам. Желательно позаботиться о том, чтобы диалог с компьютером был удобен и понятен для пользователя настолько, чтобы им мог воспользоваться те только его создатель.
- *) Используя результаты Вашей деятельности, смоделируйте движение точки, описанное в задачах 3 и 4.
Лекция 2
Кинематика. Основные понятия
2.1. Перемещение. Средняя и мгновенная скорости

|

| (2.1) | Перемещение материальной точки за время d t. | |

| (2.2) | Средняя скорость. | ||

| (2.3) | Мгновенная скорость. | ||

|

| (2.4) | Определение мгновенной скорости по известной зависимости соответствующей координаты от времени. | |

| Рис. 2.1 Так можно находить производные функций, не умея дифференцировать, но имея на своем компьютере пакет «Математика». | |||

| 
| (2.5) | Определение координат материальной точки по известным зависимостям от времени проекций ее скоростей. | |

| Рис. 2.2 Так можно находить интегралы от многих функций, не умея дифференцировать, но имея на своем компьютере пакет «Математика». | |||
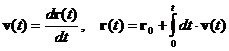
| (2.6) | Связь между координатой и мгновенной скоростью. | ||
2.2. Ускорение материальной точки

| 
| Рис.2.3 Радиус-вектор материальной точки и годограф вектора скорости. | |
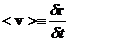


| 


| (2.7) | Связь среднего и мгновенного ускорения с мгновенной скоростью. Приведенные соотношения получаются из ранее полученной связи радиус-вектора и мгновенной скорости (2.2-2.6) заменой r®v иv®a. |
 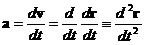
| (2.8) | Связь мгновенного ускорения с радиус-вектором. |
Пример. Движение тела по эллиптической траектории

| 
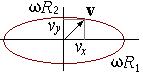
| 2.9) | Одна из возможных форм движения по эллиптической траектории. |
| 
| (2.10) | Годограф скорости при движении по эллиптической траектории. |

| (2.11) | Ускорение при движении по эллиптической траектории. |
2.3. Равноускоренное движение

| (2.12) | Ускорение при равноускоренном движении остается постоянным. |

| (2.13) | При равноускоренном движении скорость является линейной функцией времени. |
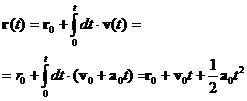
| (2.14) | При равноускоренном движении координата является квадратичной функцией времени. |
Пример. Движение тела, брошенного под углом к горизонту

| 
| (2.15) | Начальные условия и конкретный вид ускорения |

| 
| (2.16) | Зависимость от времени компонент скорости тела, брошенного под углом к горизонту. |
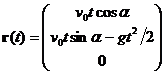
| (2.17) | Зависимость координат тела от времени. | |
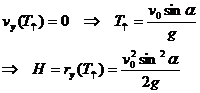
| (2.18) | Время подъема и максимальная высота подъема тела, брошенного под углом к горизонту и максима. | |

| (2.19) | Время и дальность полета тела, брошенного под углом к горизонту. | |

| (2.20) | Уравнение траектории тела, брошенного под углом к горизонту. |
2.4. Классический закон сложения скоростей и ускорений

| 
| (2.21) | Связь между радиус-векторами, задающими положение материальной точки, в разных системах отсчета. |

| (2.22) | Классический закон сложения скоростей. | |

| (2.23) | Классический закон сложения ускорений. |
2.5. Преобразования Галилея
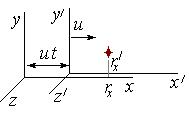
| 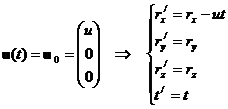
| (2.21) | Преобразования Галилея. |

| (2.22) | Классический закон сложения скоростей. |
Вопросы и задачи для самостоятельной работы
1. Найти зависимости от времени скорости и радиус-вектора материальной точки, начинающей двигаться из начала координат с направленным вертикально вниз ускорением g 0 и постоянной «тряской» Q (скоростью изменения ускорения), направленной а) горизонтально, б) вертикально вверх.
2. Найти дальность полета и максимальную высоту подъема тела над наклонной плоскостью, составляющей угол 300 к горизонту тела, брошенного под углом в 450 к этой наклонной плоскости.
3. Геометрическим местом точек, выпущенных из одной точки во всевозможных направлениях с одинаковой начальной скоростью и движущихся с одинаковым ускорением a (t), в любой момент времени является сфера. Доказать.
4. *) Решить проблему построения 3d- траекторий материальной точки по заданным зависимостям r(t), v(t), a(t). Необходимые начальные условия считать заданными.
5. *) Проверьте свое умение дифференцировать и интегрировать (на бумаге или на компьютере) на следующем тестовом примере:
На сколько сместится тело а) за T=10с, б) до полной остановки, если оно движется прямолинейно, а его скорость изменяется во времени по закону
i.  .
.
Найти ускорение тела в момент времени T. Построить графики зависимостей от времени координаты, скорости и ускорения тела.
6. Построить траекторию и годограф скорости, найти ускорение материальной точки, движущейся в плоскости по закону:
i. 
Лекция 3
Кинематика криволинейного движения
3.1. Скалярное произведение. Базис

|

| (3.1) | Определение скалярного произведения. |

|
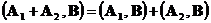
| (3.2) | Линейность скалярного произведения по его сомножителям. |

| (3.3) | Свойство векторов ортонормированного базиса. | |

| (3.4) | Вычисление скалярного произведения через координаты сектора. | |
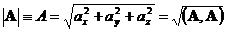
| (3.5) | Длина вектора |
3.2. Путь, проходимый материальной точкой

|

| (3.6) | Математическое определение длины отрезка кривой. |
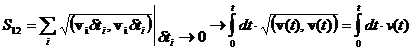
| (3.7) | Вычисление длины отрезка траектории по известной скорости. |
Пример. Путь, пройденный телом, брошенным под углом к горизонту

| (3.8) | Вычисление модуля вектора скорости. |

| (3.9) | Вычисление интеграла при помощи пакета «Математика». |

| (3.10) | Длина траектории тела, брошенного под углом к горизонту. |
3.3. Векторное произведение

|

| (3.11) | Определение векторного произведения. |

|


| (3.12) | Смешанное скалярно-векторное произведение и его основное свойство. |


| (3.13) | Свойство линейности векторного произведения по его сомножителям и идея доказательства этого свойства. | |
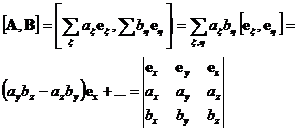
| (3.14) | Вычисление векторного произведения по декартовым координатам перемножаемых векторов. | |

| (3.15) | Правило «bac-cab» и идея его доказательства. |
3.4. Угловая скорость и угловое ускорение

| 


| (3.16) | Определение угловой скорости. |

|

| (3.17) | Связь угловой и линейной скорости. |

| (3.18) | Угловое ускорение. | |

| (3.19) | Связь линейного и углового ускорений. |
Пример. Движение тела по дуге окружности

| (3.20) | Движение по окружности с постоянной угловой скоростью. |

| (3.21) | Описание равномерного вращения по окружности в декартовых координатах. |

| (3.22) | Нормальное (центростремительное) ускорение при равномерном вращении по окружности. |

| (3.23) | Равноускоренное движение по окружности. |
3.5. Нормальное и тангенциальное ускорения

| 
| (3.24) | Разложение ускорения на нормальное и тангенциальное. |
Пример. Движение тела, брошенного под углом к горизонту: нормальное и тангенциальное ускорения

| (3.25) | Нормальное и тангенциальное ускорения тела, брошенного под углом к горизонту. |
Вопросы и задачи для самостоятельной работы
1. Первоначально покоившаяся материальная точка начинает двигаться по окружности радиусом R с постоянным угловым ускорением. Получить явные зависимости от времени декартовых координат и проекций линейной скорости и ускорения (r x(t), v x(t), a x(t), x = x, y). Убедитесь непосредственным сравнением в справедливости соотношений (3.21) для рассмотренного случая.
2. Рассмотрите движение материальной точки с постоянной угловой скоростью w0 по спирали («окружности», радиус которой увеличивается со временем по линейному закону: R (t)= u t). Как направлены скорость и ускорение материальной точки в каждый момент времени? Чему равны их модули? Получите ответы, используя явные выражения (3.19) для декартовых координат и проекций скорости и сравните результаты с общими формулами
3. Найти радиус кривизны траектории тела, брошенного под углом к горизонту в каждой точке его траектории.
4. Небольшое тело, подвешенное на невесомой нерастяжимой нити длиной L, начинает двигаться без начальной скорости из положения, в котором нить составляла угол 450 с вертикалью. Определить величину нормального и тангенциального ускорений в произвольной точки траектории.
5. *Тело движется с постоянной по модулю скоростью v по траектории, представляющей собой синусоиду с заданными параметрами y(x)= A sin(kx). Определить нормальное и тангенциальное ускорения тела в каждой точке траектории.
6. * Определить траекторию тела и найти пройденный им путь и перемещение за время T =p/w, если его координаты изменяются по закону:
x(t)=(R0/5)cos(5wt)
y(t)=(R0/3)sin(3wt).
Лекция 4
Основы динамики материальной точки
4.1. Законы Ньютона

|

| (4.1) | Первый закон Ньютона: существуют инерциальные системы отсчета (т.е. такие системы, в которых свободные тела движется без ускорений). |

| (4.2) | Второй закон Ньютона (ускорение тела пропорционально приложенной к нему силе) и определение массы. | |

| (4.3) | Свойства массы, постулируемые в классической механике. | |

|


| (4.4) | Третий закон Ньютона: при взаимодействии двух тел всегда возникают силы, приложенные к каждому из них, равные по величине и противоположно направленные. |
4.2. Импульсная формулировка второго закона Ньютона

| (4.5) | Определение импульса материальной точки. |
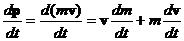
| (4.6) | Скорость изменения импульса. |

| (4.7) | Импульсная формулировка второго закона Ньютона. |

| (4.8) | Второй закон Ньютона в случае движения тела с переменной массой. |
4.3. Второй закон Ньютона как уравнение движения

| (4.9) | Упрощенная схема решения основной и обратной задачи механики. |

| (4.10) | Второй закон Ньютона как уравнение движения (дифференциальное уравнение второго порядка в обыкновенных производных). |

| (4.11) | Основные силы, рассматриваемые в классической физике (использована система единиц Гаусса). |
4.4. Прямая задача механики
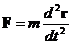
| (4.12) | Решение прямой задачи механики. |
Пример. Суперпозиция гармонических колебаний одинаковой частоты

| (4.13) | Движение, представляющее собой суперпозицию гармонических колебаний вдоль каждой из координат, происходит под действием силы, линейной по смещению. |
4.5. Обратная задача механики (случай явной зависимости силы от времени)

| (4.14) | Решение основной задачи механики в случае силы, явно зависящей от времени, и только от него. |
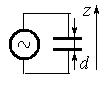
Пример. Электрон во внешнем электрическом поле, изменяющемся во времени по гармоническому закону
| 
| (4.15) | Сила, действующая на электрический заряд, помещенный в конденсатор, на обкладки которого подано переменное напряжение. |

| (4.16) | Движение электрического заряда в пространственно однородном электростатическом поле, изменяющемся во времени по гармоническому закону. |
Вопросы и задачи для самостоятельной работы
1. Рассмотреть движение электрона в плоском конденсаторе емкости C, первоначально заряженном до напряжения U 0 и разряжающемся через сопротивление R. Первоначально электрон покоился в начале координат.
2. Как будет изменяться во времени скорость вертолета, неподвижно в висевшего на высоте H над поверхностью Земли, если сила вертикальной тяги его двигателя изменяется во времени по закону
 ?
?
При каких условиях вертолет не ударится о поверхность Земли?
3*. Попытайтесь создать программу, моделирующую движение материальной точки под действием силы, изменяющейся во времени по произвольно задаваемому пользователем закону.
4*.Смоделируйте движение тела, описываемого системой уравнений (4.12). Что представляет собой траектория тела в этом случае? Можете ли Вы подтвердить свою догадку, основанную на компьютерной модели, аналитическими расчетами или какими-то другими вескими соображениями?
5. Координата тела, движущегося по прямолинейной траектории, изменяется во времен по закону:

Найти зависимость действующей на тело силы от скорости.
6. В разделе, посвященном специальной теории относительности, будет показано, что масса тел зависит от скорости по закону
 .
.
Найдите зависимости от времени координаты и скорости первоначально покоившегося тела, испытывающего воздействие постоянной силы.
Лекция 5
Одномерное движение под действием сил, зависящих от положения и скорости тела, в простейших случаях
5.1. Случай силы, зависящей только от скорости и сонаправленной с ней

| (5.1) | Общий вид силы, зависящей от скорости и направленной вдоль ее направления. |

| (5.2) | Решение задачи о движении тела под действием силы (5.1). |
Пример. Движение тела под действием сил вязкого трения

| (5.3) | Сила вязкого трения. |
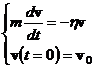
| (5.4) | Уравнение движения и начальное условие. |

| (5.5) | Решение задачи (5.4) методом (5.2). |
5.2 Падение тела в вязкой среде
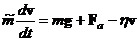
| (5.6) | Уравнение движения тела, падающего в вязкой среде. В левую часть уравнения включена присоединенная масса. | |

| 
| (5.7) | Проекция уравнения движения (5.6) на вертикальную ось. |

| (5.8) | Решение дифференциального уравнения (5.7). | |

| (5.9) | Определение константы интегрирования по начальному условию. | |

| 
| (5.10) | Построение графика зависимости v(t). |

| (5.11) | Зависимость от времени координаты тела, падающего в вязкой среде. |
5.3. Одномерное движение частицы под действием силы, зависящей от координаты

| (5.12) | Уравнение одномерного движения частицы в поле потенциальных сил. |
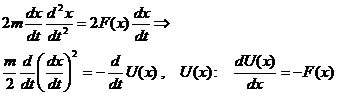
| (5.13) | Первый интеграл движения. |

| (5.14) | «Закон сохранения механической энергии» — результат интегрирования уравнения (15.13). |

| (5.15) | Связь скорости с координатой в случае одномерного движения в поле потенциальных сил. |

| (5.16) | Искомая связь координаты тела и времени движения. |
Пример. Гармонический осциллятор

|

| (5.17) | Зависимость силы и потенциальной энергии от координаты в случае гармонического осциллятора. |
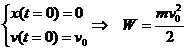
| (5.18) | Возможный вариант начальных условий и соответствующая ему полная механическая энергия осциллятора. | |

| (5.19) | Подстановка значений в общую формулу (5.16). | |

| Рис. 5.2. Вычисление интеграла типа (5.19) с помощью пакета «Математика» | ||
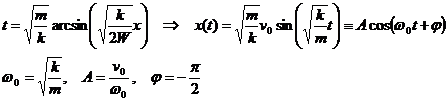
| (5.20) | Окончательное решение задачи и его запись в стандартных обозначениях. |
Движение, описываемое линейным дифференциальным уравнением с постоянными коэффициентами

| 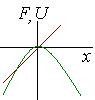
| (5.21) | Уравнение движения вблизи точки неустойчивого равновесия и стандартные обозначения для записи уравнения второго порядка. |
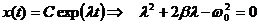
| (5.22) | Вид пробного решения уравнения (5.21) и характеристическое уравнение для l. | |

| (5.23) | Два линейно независимых решения уравнения (5.22). |

| (5.24) | Общее решение уравнения (5.22) и конкретное решение в случае тела, выпущенного из точки неустойчивого равновесия с заданной начальной скоростью. |
5.5. Движение, описываемое нелинейным дифференциальным уравнением (реальный маятник)

| 
| (5.25) | Уравнение движения реального маятника. |

| (5.26) | Уравнение в стандартных обозначениях. | |

| Рис. 5.3. При малых начальных скоростях колебания оказываются близкими к гармоническим, поскольку входящий в уравнение движения синус может быть аппроксимирован линейной функцией, что приводит к уравнению, тождественному уравнению гармонических колебаний (5.17). | ||

| Рис. 5.4. При приближении начальной скорости к критическому значению, соответствующему энергии перехода системы в состояние неустойчивого равновесия, колебания начинают резко отличаться от гармонических: в области изменения направления движения (поворота) тело проводит аномально большое время. | ||

| Рис. 5.5. При превышении начальной скоростью критического значения колебательный режим принципиально меняется: маятник начинает вокруг точки подвеса с угловой скоростью, сильно зависящей от положения груза. | ||

| Рис. 5.6. При больших начальных скоростях незначительные изменения скорости, вызванные действием на маятник силы тяжести, становятся малосущественными. |
5.6. Классическая частица в одномерной потенциальной яме

| 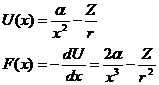
| (5.27) | Потенциальная яма, обусловленная кулоновскими взаимодействиями и центробежными эффектами. | |
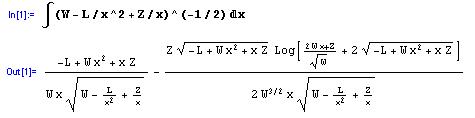
| Рис. 5.7. Попытка получения аналитического решения для движения в потенциальной яме. Обратить уравнение относительно времени при помощи пакета «Математика» не приносит успеха. | |||

|
Рис. 5.8. Программа численного интегрирования уравнения движения (случай финитного движения).

| 
|
Рис. 5.9. Фазовая диаграмма и зависимость от времени координаты частицы, совершающей финитное движение в потенциальной яме.

| 
|
Рис. 5.11. Фазовая диаграмма и зависимость от времени координаты частицы, совершающей инфинитное движение в потенциальной яме.
Вопросы и задачи для самостоятельной работы
1. Решить задачу о зависимости от времени координаты тела, движущегося пол действием силы вязкого трения, величина которой зависит от скорости по квадратичному закону:
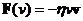
Построить графики зависимости от времени координаты, скорости и ускорения тела, падающего с вязкой среде.
2. Решить задачу об одномерном движении тела под действием упругих сил в случае произвольных начальных условий (v0¹0, x0¹0). Попытайтесь получить графики зависимости от времени координаты и скорости частицы при различных начальных условий, решая дифференциальное уравнение движения при помощи какого-либо стандартного математического пакета.
3. Исследовать движение частицы под действием упругих сил при наличии вязкого трения. Какие принципиально различные формы движения могут существовать в этом случае?
4. *Основываясь на полученных в п.5.4 результатах постройте примерные графики зависимостей натяжения нити от времени и угловой скорости от угла отклонения («фазовую траекторию» нелинейного маятника) в четырех рассмотренных на лекции предельных случаях. Проверьте правильность своих рассуждений на компьютерных моделях.
5. ** Рассмотрите одномерное движение частицы в поле сил, потенциальная энергия которых имеет вид, изображенный на рис.:

При анализе каких систем может оказаться полезным полученные вами решения?
Лекция 6
Примеры движения в трехмерном пространстве под действием сил,
зависящих от положения и скорости тела
6.1. Движение тела, брошенного в вязкой среде под углом к горизонту

| (6.1) | Укороченная запись результирующей силы, использующая эффективную массу. |

| (6.2) | Постановка задачи и выбор системы отсчета. Здесь m/ - масса жидкости или газа, вытесненной телом. |

| (6.3) | Результат проектирования векторного равенства (5.6) на «стандартную» систему координат. |

| (6.4) | Пример решения одного из дифференциальных уравнений, составляющих систему (5.7). |

| (6.5) | Зависимость от времени скорости тела, брошенного под углом к горизонту в вязкой среде. |

| Рис.5.1. Зависимости от времени горизонтальной и вертикальной составляющих скоростей тела, брошенного в вязкой среде под углом к горизонту (случай плотности тела, превосходящей плотность среды). |
6.2. Движение тела под действием силы Лоренца


| 
| (6.6) | Сила Лоренца, действующая на электрический заряд, движущийся в магнитном поле. | |

| (6.7) | Уравнение движение электрического заряда в однородном постоянном магнитном поле | ||

|

| (6.8) | Возможность разложения движения заряда в однородном магнитном роле на два независимых: равномерное (вдоль линий поля) и ускоренное (в плоскости, перпендикулярной линиям B). | |

| (6.9) | Отсутствие тангенциального ускорения при движении заряда в однородном магнитном поле. | ||

| (6.10) | Радиус кривизны траектории заряженной частицы, влетающей в магнитное поле перпендикулярно его линиям. | ||
Пример. Технические использования свойств движения заряда в однородном магнитном поле.

| (6.11) | Независимость от скорости периода обращения нерелятивистских зарядов вокруг линий магнитного поля используется в циклотронных ускорителях. |

| (6.12) | Разложение движения в магнитном поле в суперпозицию равномерных поступательного и вращательного используется при фокусировке пучков заряженных частиц. |

| (6.13) | Зависимость радиуса кривизны траектории частицы в магнитном поле от ее кинетической энергии, заряда и массы может использоваться для селекции частиц по этим параметрам. |
6.3. Движение заряженной частицы в скрещенных постоянных магнитном и электрическом полях

|

| (6.14) | Уравнение движения нерелятивистской частицы в скрещенных полях. |
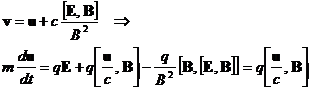
| (6.15) | Замена переменных, приводящая уравнение (6.14) к стандартному уравнению вращения заряда в магнитном поле. | |

| (6.16) | Скорость дрейфа поперек линий поля. |
6.4. Движение в кулоновском поле
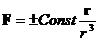
| (6.17) | Общий вид силы, соответствующий кулоновскому полю. |

| (6.18) | Простейшая схема численного интегрирования уравнения движения (на практике используются более эффективные алгоритмы) |

| Рис. 6.1. Траектории движения материальных точек в кулоновском поле тяготения: эллипсы, параболы и гиперболы (приведены результаты численного интегрирования уравнения движения методом Рунге-Кутта 4 порядка). | |

| Рис. 6.2. Траектории движения материальных точек в кулоновских полях притяжения и отталкивания на примере пролета вблизи ядра невзаимодействующих друг с другом частиц, несущих положительный, отрицательный и нулевой заряды (приведены результаты численного интегрирования уравнения движения методом Рунге-Кутта 4 порядка). |
6.5. Примеры численного интегрирования движения в центральных и произвольных силовых полях
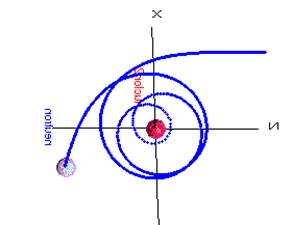
| Рис. 6.3.
Траектории движения материальных точек в центральном поле тяготения для частного случая сил, соответствующих потенциалу Юкавы:
 (приведены результаты численного интегрирования уравнения движения методом Рунге-Кутта 4 порядка).
(приведены результаты численного интегрирования уравнения движения методом Рунге-Кутта 4 порядка).
|
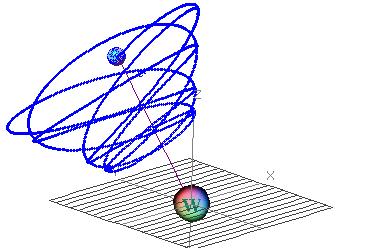
| Рис. 6.4. Пример траектории движения материальной точек в нецентральном поле, представляющем собой суперпозицию кулоновского поля тяготения и магнитного поля гипотетической частицы — магнитного монополя (приведены результаты численного интегрирования уравнения движения методом Рунге-Кутта 4 порядка). |
Вопросы и задачи для самостоятельной работы
1. *Попытайтесь рассмотреть движение заряженной частицы в суперпозиции постоянных электрического и магнитного полей, если а) поля с