Пригодность линейного уравнения регрессии для решения задачи поиска области оптимума проверяется методом, изложенным в гл. II, § 6. Сравниваются две дисперсии — одна показывает рассеяние средних опытных данных переменной состояния  относительно тех значений переменной состояния
относительно тех значений переменной состояния 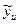 , которые предсказаны полученным линейным уравнением регрессии. Эта дисперсия называется дисперсией адекватности и рассчитывается по формуле:
, которые предсказаны полученным линейным уравнением регрессии. Эта дисперсия называется дисперсией адекватности и рассчитывается по формуле:
 (26)
(26)
где m — число параллельных опытов; N — число строк матрицы планирования; l — число членов в уравнении регрессии, оставшихся после оценки значимости.
Вторая дисперсия — это ошибка опыта. Адекватность проверяют, оценивая отношение
 (27)
(27)
по критерию Фишера
 (28)
(28)
для степеней свободы fад = N — l, f0 = N (m — 1) и заданного уровня значимости q. Если выполняется условие (28), то линейное уравнение регрессии признается адекватным, т. е. рассеяние экспериментальных данных переменной состояния относительно уравнения регрессии того же порядка, что и рассеяние, вызванное случайными изменениями в объекте исследования (ошибка опыта)
Таблица 7. Формула расчета ПФЭ2n
| Блоки | Формулы расчета | Обозначения |
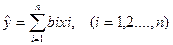 Или
Или

|  – переменная состояния расчетная); – переменная состояния расчетная);
 – факторы; – факторы;
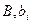 – коэффициенты уравнения регрессии; – коэффициенты уравнения регрессии;
 – число факторов; – число факторов;
 – переменная состояния (экспериментальная); – переменная состояния (экспериментальная);
 – транспонированная матрица X; – транспонированная матрица X;
 – число опытов – число опытов
 – построчная дисперсия; – построчная дисперсия;
 –переменная состояния (в параллельных опытах) –переменная состояния (в параллельных опытах)
 – расчетные значения критерия Кохрена; – расчетные значения критерия Кохрена;
 – число параллельных опытов – число параллельных опытов
 – табличное значение критерия Кохрена; – табличное значение критерия Кохрена;
 – число степеней свободы; – число степеней свободы;
 – уровень значимости – уровень значимости
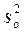 – ошибка опыта (дисперсия воспроизводимости); – ошибка опыта (дисперсия воспроизводимости);
 – дисперсии коэффициентов; – дисперсии коэффициентов;
 – расчетное значение критерия Стьюдента; – расчетное значение критерия Стьюдента;
 – среднеквадратичные отклонения – среднеквадратичные отклонения
 – табличное значение критерия Стьюдента; – табличное значение критерия Стьюдента;
 – число степеней свободы; – число степеней свободы;
 – дисперсия адекватности; – дисперсия адекватности;
 – расчетное значение критерия Фишера – расчетное значение критерия Фишера
 – число степеней свободы – число степеней свободы
| |
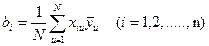
| ||
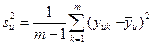
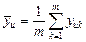

| ||
| 3а | Условие однородности

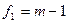

| |


| ||

| ||
| 5а | Условие значимости коэффициентов


| |


| ||
| 6а | Условие адекватности модели
 (q, f1,f2) (q, f1,f2)

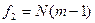
|

Рис. 4. Алгоритм расчета и анализа математической модели
При расчете Fp предполагается, что  >
>  . Однако на практике бывает, что
. Однако на практике бывает, что  . Тогда вывод об адекватности модели может быть сделан без проверки условия (23).
. Тогда вывод об адекватности модели может быть сделан без проверки условия (23).
8. Принятие решений.
При невыполнении условия (23), т. е. при неадекватной линейной модели наиболее часто принимают решение об уменьшении интервалов варьирования факторов и повторении эксперимента. Такое решение может привести к появлению незначимых коэффициентов. Очень эффективно включать в план эксперимента новый фактор из числа тех, которые в предварительном эксперименте отсеялись, побыли близки по своему эффекту к оставшимся факторам.
Если условие (23) выполняется, то адекватный линейный полином можно использовать для поиска области оптимума объекта исследования.
Блок-схема алгоритма расчета представлена на рис 4. Все расчетные формулы сведены в табл. 7.
ПРИЛОЖЕНИЕ 1
Процентные точки распределения
| q f | 99,5% | 97,5% | 95% | 5% | 2,5% | 0,5% |
0,39  10-4 10-4
| 0,98  10-3 10-3
| 0,39  10-2 10-2
| 3,841 | 5,024 | 7,879 | |
| 0,010 | 0,050 | 0,103 | 5,991 | 7,378 | 10,597 | |
| 0,072 | 0,216 | 0,352 | 7,815 | 9,348 | 12,838 | |
| 0,207 | 0,484 | 0,711 | 9,488 | 11,143 | 14,860 | |
| 0,412 | 0,831 | 1,145 | 11,070 | 12,832 | 16,750 | |
| 0,676 | 1,237 | 1,635 | 12,592 | 14,449 | 18,548 | |
| 0,989 | 1,690 | 2,167 | 14,067 | 16,013 | 20,278 | |
| 1,344 | 2,! 80 | 2,733 | 15,507 | 17,535 | 21,955 | |
| 1,735 | 2,700 | 3,325 | 16,919 | 19,023 | 23,589 | |
| 2,156 | 3,247 | 3,940 | 18,307 | 20,483 | 25,188 | |
| 2,630 | 3,816 | 4,575 | 19,575 | 21,920 | 26,757 | |
| 3,074 | 4,404 | 5,226 | 21,026 | 23,336 | 28,300 | |
| 3,565 | 5,009 | 5,892 | 22,362 | 24,736 | 29,819 | |
| J4 | 4,075 | 5,629 | 6,571 | 23,685 | 26,119 | 31,319 |
| 4,601 | 6,262 | 7,261 | 24,996 | 27,448 | 32,801 | |
| 5,142 | 6,908 | 7,962 | 26,296 | 28,845 | 34,267 | |
| 5,697 | 7,564 | 8,672 | 27,587 | 30,191 | 35,718 | |
| 6,256 | 8,231 | 9,390 | 28,869 | 31,526 | 37,156 | |
| 6,844 | 8,907 | 10,117 | 30,144 | 32,852 | 38,582 | |
| 7,434 | 9,591 | 10,851 | 31,410 | 34,170 | 39,997 | |
| 8,034 | 10,283 | 11,591 | 32,671 | 35,479 | 41,401 | |
| 8,643 | 10,982 | 12,338 | 33,924 | 36,781 | 42,796 | |
| 9,260 | 11,688 | 13,091 | 35,172 | 38,076 | 44,181 | |
| 9,886 | 12,401 | 13,848 | 36,145 | 39,364 | 45,558 | |
| 10,520 | 13,120 | 14,611 | 37,652 | 40,646 | 46,928 | |
| 11,160 | 13,844 | 15,379 | 38,885 | 41,923 | 48,290 | |
| 11,808 | 14,573 | 16,151 | 40,113 | 43,194 | 49,645 | |
| 12,461 | 15,308 | 16,928 | 41,337 | 44,461 | 50,993 | |
| 13,121 | 16,047 | 17,708 | 42,557 | 45,722 | 52,336 | |
| 13,787 | 16,791 | 18,493 | 43,773 | 46,979 | 53,672 |
Процентные точки распределения Стьюдента
| q f | 10% | 5% | 2% | 1% | q f | 10% | 5% | 2% | 1% |
| 6,31 | 12,71 | 31,82 | 63,66 | 1,94 | 2,45 | 3,14 | 3,71 | ||
| 2,92 | 4,30 | 6,96 | 9,92 | 1,89 | 2,36 | 3,00 | 3,50 | ||
| 2,35 | 3,18 | 4,54 | 5,84 | 1,86 | 2,31 | 2,90 | 3,36 | ||
| 2,13 | 2,78 | 3,75 | 4,60 | 1,83 | 2,26 | 2,82 | 3,25 | ||
| 2,02 | 2,57 | 3,36 | 4,03 | 1,81 | 2,23 | 2,76 | 3,17 |