Методические указания по решению задач

Методические указания по выполнению контрольной работы

В соответствии с учебным планом по дисциплине «Теория вероятностей и математическая статистика» для студентов заочного отделения направления обучения «Экономика» предусмотрено выполнение контрольной работы. Контрольную работу студенты выполняют дома по назначенному варианту. Оформленная в соответствии с требованиями контрольная работа сдается для проверки преподавателю в установленные сроки. Для того чтобы работа была своевременно проверена, при необходимости доработана и сдана повторно на проверку надо сдать работу значительно раньше установленного критического срока.

Если контрольная работа имеет существенные недочеты и требуется повторное решение задач, то она получает оценку «Не зачтено». Такую работу необходимо переделать в соответствии с замечаниями преподавателя, проверившего работу. Доработанная контрольная выполняется в той же тетради или новой с надписью «Повторная» и сдается на повторную проверку вместе с первоначальной работой.

Если работа оценивается положительно, то на ней делается надпись «Зачтено». При этом в работе могут иметь место отдельные недочеты или ошибки, которые необходимо устранить, выполнив работу над ошибками в той же тетради и представить ее преподавателю.

К экзамену допускаются только те студенты, которые успешно выполнили контрольную работу.

Требования к оформлению контрольной работы

Задачи контрольной работы следует выполнять в том порядке, в каком они даны в индивидуальном задании. При оформлении контрольной работы необходимо переписать условие задачи, а затем после слова «Решение» привести решение. Каждый этап решения задачи должен содержать подробные объяснения. Используемые формулы должны записываться с пояснением обозначений. Окончательный ответ надо выделить и сформулировать словесно.

При расчете необходимых показателей результаты вычислений округлять до сотых в соответствии с правилами округления. Поля, в которой выполняется работа, должны быть не менее 2 см.

Контрольная работа может быть представлена как в печатном варианте так и в рукописном и в электронном. Контрольная работа должна быть оформлена аккуратно, написано разборчиво без помарок и зачеркиваний. Не рекомендуется произвольно сокращать слова (допускаются лишь общепринятые сокращения). Все приводимы таблицы и графики надо оформлять и подписывать в соответствии с правилами, принятыми в статистике.

В конце работы указывается список используемой литературы, ставится дата ее окончания и подпись.

Вариант контрольной работы назначается преподавателем согласно порядковому номеру студента в журнале учета успеваемости. Контрольная работа не рассматривается, если ее вариант не соответствует назначенному варианту.

 

Варианты контрольной работы

Номер варианта	Задача 1	Задача 2	Задача 3	Задача 4	Задача 5	Задача 6
№ задачи

Методические указания по решению задач

Приступая к выполнению контрольной работы, рекомендуется ознакомиться с соответствующими разделами программы курса и методическими указаниями, изучить рекомендуемую учебную литературу.

 

При решении задачи 1 необходимо изучить теоретический материал по темам «Случайные события. Вероятность события» и «Теорема сложения и умножения вероятностей». В задачах вероятность события рассчитывается по классической формуле. При этом надо обратить внимание на применение элементов комбинаторики для подсчета числа различных комбинаций.

Пример. Из 50 сотрудников фирмы 30 человек владеют английским языком. Для участия в международной конференции случайным образом отбирается 5 человек. Какова вероятность того, что а) все выбранные сотрудники владеют английским языком; б) 3 человека из 5 выбранных знают английский язык; в) хотя бы один владеет английским языком.

 

Решение:

а) Пусть событие А – все выбранные 5 сотрудников фирмы владеют английским языком.

Согласно классическому определению Р(А) вероятность события А равна

 

,

 

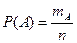где 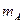- число событий, благоприятствующих событию А. Оно равно числу способов, которыми можно выбрать 5 сотрудников фирмы, владеющих английским языком, т.е. числу способов отбора 5 человек из 30. Поскольку в данном случае неважен порядок расположения 5 человек, то образуемые подмножества есть сочетания. Число сочетаний определяется по формуле

 

.

 

Напомним, что , .

 

Следовательно .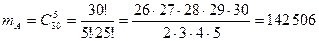

 

n - общее число возможных элементарных исходов испытания, равно числу способов, которыми можно отобрать 5 человек из 50 сотрудников банка.

 

.

 

Искомая вероятность равна: .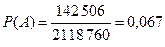

 

б) Пусть событие В - 3 человека из 5 выбранных знают английский язык.

 

Вероятность события В равна .

 

Найдем 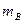- число исходов, благоприятствующих событию В. Среди выбранных пяти сотрудников фирмы три человека владеют английским языком, а два нет. Число таких исходов равно числу способов, которыми можно отобрать трех человек из 30, владеющих английским, и два человека из 20 не владеющих английским. Поскольку порядок расположения отобранных сотрудников неважен, то число исходов равно:

 

.

 

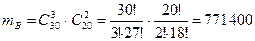Искомая вероятность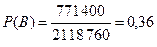

 

в) Пусть событие С - хотя бы один человек из пяти выбранных владеет английским языком.

 

1 способ.

Событие С можно представить как сумму следующих событий:

С₁ – из пяти отобранных сотрудников английским владеет один человек;

С₂ - из пяти отобранных сотрудников английским владеют два человека;

С₃ - из пяти отобранных сотрудников английским владеют трое;

С₄ - из пяти отобранных сотрудников английским владеют четверо;

С₅ - из пяти отобранных все сотрудники владеют английским.

Тогда С = С₁ + С₂ + С₃ + С₄ + С₅. Следовательно, число исходов 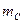, благоприятствующих событию С равно:

.

Аналогично предыдущему пункту задачи рассчитаем число исходов, благоприятствующих событиям С₁, С₂, С₃, С₄, С₅.

 

;

;

;

;

.

 

.

 

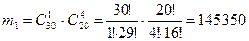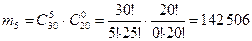Искомая вероятность .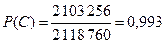

 

2 способ.

Как известно, 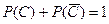. Тогда 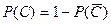, где - событие противоположное событию С – ни один из пяти сотрудников не владеет английским языком.

Число исходов, удовлетворяющих событию , равно числу способов, которыми можно отобрать пять человек из 20 не владеющих английским языком.

 

.

 

Тогда .

 

Искомая вероятность .

Ответ: вероятность того, что а) все выбранные сотрудники владеют английским языком равна 0,067; б) 3 человека из 5 выбранных знают английский язык равна 0,36; в) хотя бы один сотрудник фирмы из выбранных владеет английским языком равна 0,997.

 

 

Задача 2 составлена на применение формул вычисления вероятности наступления определенного числа события в n независимых испытаниях. При этом все испытания должны быть независимы и вероятность события в каждом испытании постоянна, т.е испытания должны удовлетворять схеме Бернулли. Применение той или иной формулы вычисления вероятности появления события А k раз в n независимых испытаниях определяется числом k.

Пример. Вероятность того, что посетитель продуктового магазина купит молоко равна 0,7. Определите вероятность того, что а) из 10 покупателей ровно 4 купят молоко; б) из 80 покупателей ровно 50 купят молоко; в) из 100 покупателей от 65 до 80 человек купят молоко.

 

 

Решение.

а) В данной задаче испытанием является посещение покупателем магазина. При этом возможны два исхода каждого испытания: покупатель купит молоко или нет. Пусть событие А – посетитель магазина купит молоко.

Поскольку а) все n испытаний независимы, так как вероятность того, что один посетитель магазина купит молоко не зависит от того купит ли другой посетитель молоко, б) вероятность события – покупка молока в каждом испытании постоянна, то испытания удовлетворяют схеме Бернулли. Число k – невелико, следовательно, вероятность того, что из 10 покупателей молоко приобретут ровно 4, можно определить по формуле Бернулли:

 

,

 

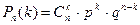где р=Р(А) – вероятность наступления события А в каждом испытании;

q=1-p – вероятность противоположного события ().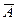

По условию задачи n=10, k=4, p=0,7, q=0,3.

 

Искомая вероятность .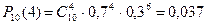

 

б) Определим вероятность того, что из 80 покупателей магазина 50 купят молоко. По условию задачи n=80, k=50, p=0,7, q=0,3. Так как проводится достаточно большое число испытаний n=80, то искомую вероятность будем вычислять с помощью асимптотической формулы – локальной теоремы Муавра-Лапласа:

,

 

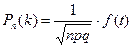где ;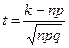

 

- функция Гаусса (приложение 1)

 

Основные свойства f(t), необходимые для применения рассматриваемой теоремы:

1. f(t) – четная функция, т.е. f(t) = f(-t);

2. f(t) – монотонно убывающая функция, т. е. f(t) →0 при t →±∞; при t >5 можно считать f(t) ≈ 0

 

Подставив исходные данные получим:

 

.

 

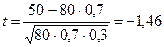По таблице приложения 1 найдем значение функции Лапласа в точке t:

f (-1,46) = f (1,46) = 0,1374.

 

Искомая вероятность .

 

в) Для расчета вероятности того, что из 100 покупателей от 65 до 80 человек купят молоко воспользуемся асимптотической формулой – интегральной теоремой Муавра-Лапласа:

 

,

 

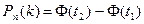где , .

 

– функция Лапласа (приложение 2).

 

Отметим основные свойства Ф(t), необходимые для применения данной теоремы:

1. Ф(t) – нечетная функция, т. е. Ф(- t) = - Ф(t).

2. Ф(t) - монотонно возрастающая функция, т. е. Ф(t)→0,5, при t →∞;при t >5 можно считать Ф(t)≈0,5.

 

По условию задачи n=100, а=65, b=80, p=0,7, q=0,3. Вычислим t₁ и t₂.

 

; .

 

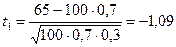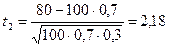По таблице приложения 2 находим значение функции Лапласа в точках t₁ и t₂, учитывая что функция Лапласа нечетная получаем искомую вероятность:

 

.

 

 

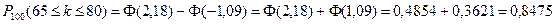При решении задачи 3 следует обратиться к теме «Дискретные случайные величины». Особое внимание надо уделить способам задания закона распределения дискретной случайной величины и расчету ее числовых характеристик, выражающих наиболее существенные черты распределения в сжатой форме, основными из которых являются математическое ожидание, дисперсия и среднеквадратическое отклонение.

 

Пример. Вероятность опоздания поезда равна 0,4. Написать биномиальный закон распределения числа опоздавших поездов из четырех, прибывших на станцию. Построить график распределения вероятностей. Найти функцию распределения числа опоздавших поездов и построить ее график. Рассчитать математическое ожидание, дисперсию и среднеквадратическое отклонение.

 

Решение:

Дискретная случайная величина Х – число опоздавших поездов из четырех. Она может принимать значения x₁ =0 (ни один поезд не опоздал), x₂ =1(опоздал один поезд), x₃ =2 (опоздали два поезда), x₄ =3 (опоздали три поезда), x₅ =4 (опоздали четыре поезда). Опоздание одного поезда не зависит от опоздания другого, вероятность опоздания поезда постоянна и не меняется от поезда к поезду. Поэтому для вычисления вероятности каждого из события применима формула Бернулли:

 

.

 

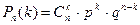По условию n=4, p=0,4, q=0,6, следовательно:

;

;

;

;

.

 

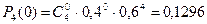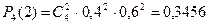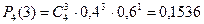Контроль: .

 

Запишем закон распределения в виде таблицы:

хi
pi	0,1296	0,3456	0,3456	0,1536	0,0256

 

Построим график распределения вероятностей. Для этого построим прямоугольную систему координат, по оси абсцисс отложим возможные значения случайной величины Х, а по оси ординат – соответствующие вероятности.

pi

хi

Рисунок 1. Полигон распределения дискретной случайной величины Х

 

Найдем функцию распределения случайной величины Х.

По определению F(x)=P(X < x).

 

При 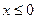случайная величина не принимает ни одного значения, тогда F(x) =0.

При 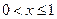в интервал (- ∞; х) попадает одно значение случайной величины х=0 с вероятностью 0,1296, следовательно F(x)=P(X=0)=0, 1296.

При в интервал (- ∞; х) попадает два значения случайной величины х =0 с вероятностью 0,1296 и х =1 с вероятностью 0,3456, следовательно F(x)=P(X=0)+Р(Х=1)=0, 1296+0,3456=0,4752.

При в интервал (- ∞; х) попадает три значения случайной величины х =0 с вероятностью 0,1296, х =1 с вероятностью 0,3456 и х =2 с вероятностью 0,3456, следовательно F(x)=P(X=0)+Р(Х=1)+Р(Х=2) = 0,1296+0,3456+0,3456=0,8208.

При в интервал (- ∞; х) попадает четыре значения случайной величины х =0 с вероятностью 0,1296, х =1 с вероятностью 0,3456, х =2 с вероятностью 0,3456 и х =3 с вероятностью 0,1531, следовательно F(x)=P(X=0)+Р(Х=1)+Р(Х=2)+Р(Х=3) =0,1296+0,3456+0,3456+0,1536=0,9744.

При в интервал (- ∞; х) попадает четыре значения случайной величины F(x)= P(X=0)+Р(Х=1)+Р(Х=2)+Р(Х=3)+P(X=4) =1.

В итоге получаем интегральную функцию:

 

 

График функции распределения имеет вид:

 

Рисунок 2. График функции распределения дискретной случайной величины Х

 

Рассчитаем основные числовые характеристики дискретной случайной величины Х.

1. Математическое ожидание дискретной случайной величины определяется по формуле:

 

,

 

и равна .

 

2. Дисперсия дискретной случайной величины.

 

1 способ.

Согласно определению, вычисляется как

 

.

 

 

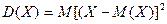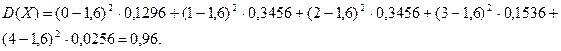
2 способ.

Рассчитывается по упрощенной формуле

 

.

 

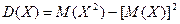где .

 

Для расчета М(Х²) составим таблицу распределения случайной величины Х²:

pi	0,1296	0,3456	0,3456	0,1536	0,0256

 

 

 

3. Среднеквадратическое отклонение

 

.

 

Рассеяние значений случайной величины Х относительно его математического ожидания, равного 1,6, составляет 0,98.

 

 

Задача 4 составлена по теме «Непрерывные случайные величины». Необходимо уяснить различия и взаимосвязь функции распределения и плотности вероятностей непрерывной случайной величины и обратить внимание на расчет математических характеристик непрерывной случайной величины и их интерпретацию.

Пример. Задана дифференциальная функция распределения случайной величины Х:

 

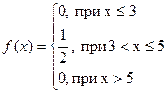
Рассчитать: 1) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х; 2) вероятность того, что в результате испытаний случайная величина примет значение большее 3 и меньшее 5. 3) Построить график функции F(х).

 

Решение:

1) Математическое ожидание непрерывной случайной величины определяется по формуле:

 

.

 

Числовая линия разбивается на три интервала точками х =3 и х =5, на каждом из которых функция плотности вероятностей принимает различные значения, следовательно

 

.

 

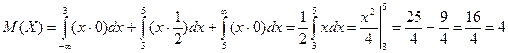Дисперсию можно вычислить двумя способами:

 

1 способ

по определению .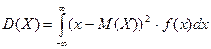

 

 

2 способ

по упрощенной формуле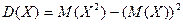

 

где

 

 

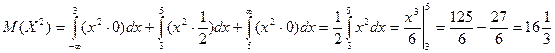
Искомая дисперсия: .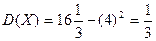

 

Среднее квадратическое отклонение вычисляется по формуле:

 

Тогда .

2) Вероятность попадания непрерывной случайной величины в определенный интервал определяется на основании свойства плотности распределения вероятностей:

,

 

т.е. .

 

3) По определению f(x)= F ^' (x), следовательно .

Так как функция плотности вероятностей имеет три интервала с различными значениями, рассмотрим функцию на каждом из этих интервалов:

при , ;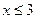

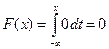при , ;

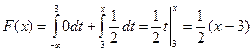при , .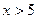

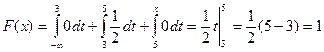Итак, функция распределения вероятностей имеет вид:

 

 

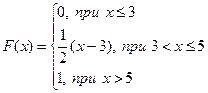
График функции распределения имеет вид:

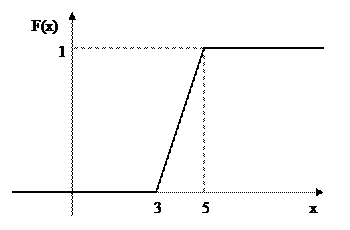
Рисунок 3. – График функции распределения вероятностей

 

 

При решении задачи 5 надо обратиться к теме «Выборочное оценивание» и «Статистическая проверка статистических гипотез». Необходимо учесть, решая задачу, что правила построения интервальной оценки генеральной средней зависят от того, известна или неизвестна дисперсия генеральной совокупности и от объема совокупности. При расчете критерия Пирсона имеются различия в методике расчета теоретических частот нормального распределения для дискретного и интервального ряда распределения эмпирических частот. Все расчеты рекомендуется представить в таблице.

 

Пример. В таблице приведены результаты анализа среднемесячной заработной платы 100 рабочих цеха:

Заработная плата, тыс. руб.	5-10	10-15	15-20	20-25	25-30	Более 30
Число рабочих

 

Найти:

а) границы, в которых с вероятностью 0,6827 заключена средняя заработная плата рабочего;

б) границы, в которых с вероятностью 0,95 заключена доля рабочих с заработной платой выше 25 тыс. руб.;

в) вероятность, с которой средняя заработная плата будет отличаться от выборочной средней не более чем на 1,5 тыс. руб;

г) используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении случайной величины Х – заработная плата рабочих с эмпирическим распределением выборки.

 

Решение.

а) Исходя из условия задачи дисперсия генеральной совокупности неизвестна и объем выборки больше 30, следовательно доверительные границы определяются по формуле:

,

 

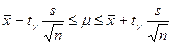где - выборочная средняя;

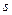– выборочное среднее квадратическое отклонение;

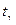- значение аргумента функции Лапласа Ф(t) (приложение 2), при котором 2Ф(t)=γ.

Выборочная средняя определяется по формуле: ,

 

где x_i – отдельные значения признака, определяемые как середина интервала;

f_i – частота признака x_i.

 

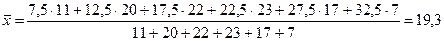тыс. руб.

 

Выборочная дисперсия рассчитывается как: .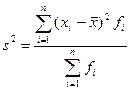

 

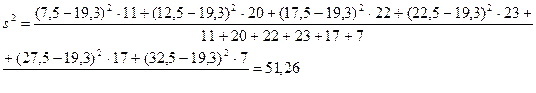
Выборочное среднее квадратическое отклонение:

тыс. руб.

По таблице функции Лапласа (приложение 2)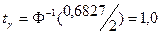

Подставляя рассчитанные значения в формулу доверительного интервала получаем:

 

,

 

.

 

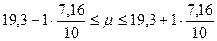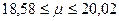Таким образом, средняя заработная плата рабочего цеха находится в пределах от 18,58 до 20,02 тыс. рублей с вероятностью 0,6827.

 

б) Построение доверительного интервала с заданной надежностью γ для генеральной доли или вероятности р при достаточно больших объемах выборки (n>30) осуществляется по формуле:

 

,

 

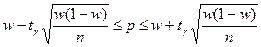где w – выборочная доля, рассчитанная как , m - число рабочих с заработной платой выше 25 тыс. руб., n – всего рабочих.

Выборочнаядоля равна: .

По таблице функции Лапласа (приложение 2) .

Искомые границы:

 

;

 

.

 

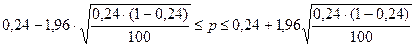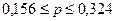Следовательно, генеральная доля рабочих с заработной платой выше 25 тыс. руб. находится в пределах от 0,156 до 0,324 с доверительной вероятностью 0,95.

 

в) Поскольку средняя заработная плата отличается от выборочной не более чем на 2 тыс. руб., то δ = 1,5. Точность оценивания генеральной средней при неизвестной дисперсии (при n>30) определяется как

 

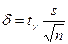и ,

 

.

 

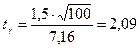По таблице функции Лапласа (приложение) вероятность γ=2Ф(t) равна γ=2Ф(2,09) = 0,4817ּ2 = 0,9634.

Итак, вероятность, с которой средняя заработная плата будет отличаться от выборочной средней не более чем на 1,5 тыс. руб. равна 0,9634.

 

г) Для проверки гипотезы о согласовании эмпирического распределения заработной платы рабочих с нормальным законом распределения надо рассчитать наблюдаемое значение критерия Пирсона по формуле:

 

,

 

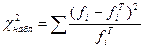где - теоретические частоты.

Так как рассматривается интервальный ряд распределения с равными интервалами, то теоретические частоты рассчитываются как

 

,

 

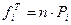где Р_i = Ф(z_i+1) – Ф(z_i) – вероятность попадания величины Х в интервал (x_i, x_i+1);

 

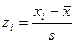, - стандартизированные значения переменной Х.

 

Учитывая, что теоретические законы, как правило, определяются для всех действительных значений случайной величины, то при получении вероятностей Р_i необходимо рассматривать расширенные интервалы, т.е. наименьшее значение z₁ полагают равным -∞, а наибольшее z_s+1 полагают равным ∞.

Для удобства все расчеты представим в таблицах 1 и 2.

 

Таблица 1. – Вспомогательная таблица расчета теоретических частот

i	Границы интервала	fi	Границы интервала	Ф(zi)	Ф(zi+1)	Pi
хi	xi+1	zi	zi+1
				-∞ -1,30 -0,60 0,10 0,80 1,49	-1,30 -0,60 0,10 0,80 1,49 ∞	-0,5000 -0,4032 -0,2252 0,0398 0,2881 0,4319	-0,4032 -0,2252 0,0398 0,2881 0,4319 0,5000	0,0968 0,1780 0,2650 0,2483 0,1438 0,0681
	Итого		-	-	-	-	-

 

Таблица 2. – Вспомогательная таблица расчета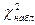

i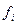
			-4 -2		0,1000 0,2222 0,6154 0,1600 0,6429 0,0000
Итого			-	-	1,7405

 

Итак, .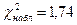

 

По таблице критических значений распределения χ² - Пирсона (приложение 3) при уровне значимости α и числе степеней свободы v = s-3 (s – число интервалов) определяется критическая точка. 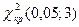= 7,8.

Так как (1,74<7,8) принимаем гипотезу о нормальном распределении генеральной совокупности Х, т.е. эмпирические и теоретические частоты распределения численности рабочих цеха по уровню заработной платы различаются незначительно.

 

 

Задача 6 составлена на расчет коэффициента корреляции и параметров уравнения парной линейной регрессии. При решении задач этого типа рекомендуется использовать упрощенный способ расчета статистических показателей.

 

Пример. По данным, приведенным в корреляционной таблице

 

Y	Х	ny
nx							n=50

 

1. оценить выборочный коэффициент корреляции и детерминации между X и Y;

2. проверить значимость генерального коэффициента корреляции при α=0,05;

3. найти выборочное уравнение прямой линии регрессии зависимости Y от Х;

4. найти выборочное уравнение прямой линии регрессии зависимости Х от Y;

Сформулировать выводы.

 

Решение.

Поскольку данные наблюдений по X и Y заданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти к условным вариантам:

 

; ,

 

где С₁, С₂ – «ложный нуль» соответственно вариант Х и Y. При этом в качестве ложного нуля выгодно принять варианту, которая расположена примерно в середине ряда и имеет наибольшую частоту.

h₁, h₂ – шаг, т.е. разность между двумя соседними вариантами, соответственно для переменных Х и Y.

Возьмем С₁ = 235, h₁ = 10;

С₂ = 84, h₂ = 4.

В результате преобразования вариант получена таблица

 

Таблица 3. – Корреляционная таблица с условными вариантами

V	U	nv
-3	-2	-1
-3
-2
-1
nu							n=50

 

В этом случае выборочный коэффициент корреляции определяется по формуле:

 

.

 

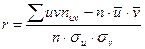Найдем и :

 

,

.

 

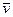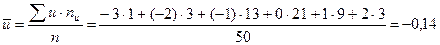Среднее квадратическое отклонение рассчитали по формулам:

 

,

.

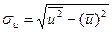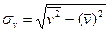Найдем 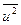и :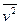

 

,

.

 

Тогда

,

.

 

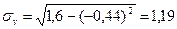Рассчитаем :

 

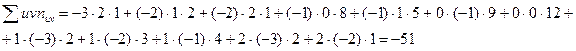
Искомый выборочный коэффициент корреляции:

 

.

 

Выборочный коэффициент корреляции показывает, что связь между переменными X и Y обратная и тесная.

 

б) Проверка значимости генерального коэффициента корреляции проводится с помощью критерия Стьюдента. Для этого рассчитывается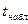

 

.

 

.

 

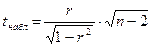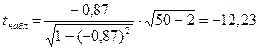По таблице критических значений Стьюдента (приложение 4) 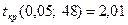. Поскольку в таблице критических значений Стьюдента представлены не все значения, то рекомендуется для получения точного значения критерия воспользоваться ППП Excel и статистической функцией СТЬЮДРАСПОБР(α, v=n-2).

Сравнивая расчетное и критическое значение t-статистики, | 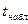| > делаем вывод о значимости генерального коэффициента корреляции с вероятностью ошибки принятия решения 0,05.

 

в) Выборочное уравн