Точно сформулируем и докажем теорему Нётер.
Рассмотрим некоторую систему, описываемую функцией Лагранжа
. (3)
Форма уравнений Лагранжа-Эйлера, получаемых из вариационного принципа с такой функцией Лагранжа, инвариантна относительно преобразований вида 
, а также и относительно более общих преобразований
(4)
включающих замену независимой переменной. Однако конкретный вид для нового выражения для действия, как функционала новых координат, зависящих от нового времени, может претерпеть при таком изменении любые изменения.
Теорема Нётер интересуется только тем случаем, когда таких изменений не происходит.
Итак, будем считать, что мы ввели совокупность зависящих от (для простоты) одного параметра l преобразований 
обобщенных координат и времени.
Используя (4), получим:
(5)
Пусть преобразования 
такие, что
(6)
т.е. образующих однопараметрическую группу. Рассмотрим бесконечно малое преобразование, отвечающее параметру 
.
Тогда
(7)
Собственно вариации обобщенных координат, происходящие при рассматриваемом преобразовании, – это разность значений 
новых координат в некоторый момент нового времени и значений старых координат 
в соответствующий момент старого времени, т.е.
. (8)
Наряду с ними удобно ввести в рассмотрение вариации формы
(9)
зависимости координат от времени, которые отличны от нуля, даже если наше преобразование затрагивает только время, а не координаты.
Для любой функции справедливо соотношение:
.
Тогда между двумя введенными видами вариаций есть соотношение, которое можно получить следующим образом: вычтем из (8) уравнение (9), получим:
,
примем во внимание, что
,
тогда имеем:
(10)
Вариации без звездочек, относящиеся к одному значению аргумента, перестановочны с дифференцированием по времени
,
в то время, как для вариаций со звездочками это, вообще говоря, неверно.
Соответствующие два вида вариаций можно ввести и для любой динамической переменной. Например, для функции Лагранжа
(11)
причем
(12)
где 
включает дифференцирование как по явно входящему времени, так и по времени, входящему неявно, через координаты и скорости.
Потребуем теперь, чтобы интеграл действия не менялся бы при нашем преобразовании, – это и есть тот исключительный случай, который требуется условием теоремы, – т.е. чтобы было
, (13)
где Т' – та же область интегрирования, что и Т во втором интеграле, но выраженная через новые переменные. Тогда подставив (11) в (13), получим
(14)
Выражаем в (15) 
через 
(11) и учитывая соотношение
,
переходя к интегрированию по t вместо t', получим:
Учитывая, что
,
получим:
(15)
Но
(16)
Найдем дифференциал
,
отсюда
(17)
Подставив (17) в (16), получим:
Под знаком первой суммы стоит уравнение Лагранжа, т.е.
Тогда имеем:
(18)
Подставим полученное значение вариации функции Лагранжа в (15), имеем:
Из (10) выразим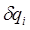 
через 
и 
:
Тогда вариация действия
(19)
Мы должны потребовать равенства этой вариации нулю. В силу произвольности области интегрирования Т из равенства нулю интеграла следует равенство нулю подынтегрального выражения, т.е. мы приходим к тому, что необходимым и достаточным условием инвариантности действия относительно преобразования (7) служит удовлетворение уравнения
.
Заменим 
и 
, используя соотношения (7) и (8), имеем:
Вынесем l за скобки и разделим на нее обе части уравнения. Окончательно получим необходимое условие:
(20)
Другими словами, из инвариантности действия относительно (7) мы получили то следствие, что величина
(21)
остается постоянной во времени. Это и есть точное утверждение теоремы Нётер.