1. 
На рисунке изображены две силы, линии действия которых, лежат в одной плоскости. Возможность определения равнодействующей по правилу параллелограмма
1. Можно
2. Нельзя
2. Две системы сил уравновешивают друг друга. При этом равнодействующие равны по модулю и направлены по одной прямой
1. Да
2. Нет
3. Численно равные силы F1 и F2 одинаково действуют на тело
 |
1.
|
2. Нет
4. Две силы по 100Н заменить одной силой 50Н. Возможность обратного действия
1. Можно
2. Нельзя
5. Возможность определения знака проекции силы F на показанную ось
 |
1. Можно
2. Нельзя
6. Величина и направление момента силы относительно точки зависит от взаимного расположения этой точки и линии действия силы
1. Да
2. Нет
7. Главный вектор и главный момент системы сил равны нулю. При этом система сил находится в равновесии.
1. Да
2. Нет
8. Центр тяжести тела является центром параллельных сил
1. Да
2. Нет
9. Возможность определения равнодействующей пространственной системы сходящихся сил графическим способом
1. Можно
2. Нельзя
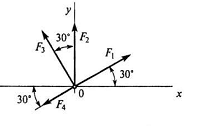
10. 
Выбрать правильную систему уравнений равновесия для системы сходящихсясил, изображенной на рисунке
1. Fx=0 F2 cos60º+F3 cos30º-F1=0
Fy=0 F2 cos30º- F3cos60º+F4=0
2. Fx=0 -F2cos60º- F3cos30º+ F1=0
Fy=0 F2cos30º- F3cos60º- F4=0
11. Рассчитать проекцию равнодействующей системы сходящихся сил на
ось у F1=16кН, F2=15 кН, F3=20 кН, F4=10 кН
1. 28,7кН
2. 30,2кН
3. 35,3кН
4. 61кН
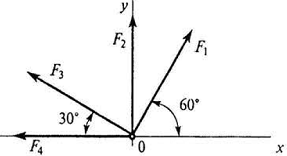
12. Рассчитать проекцию равнодействующей системы сходящихся сил на ось Ох F1=25 кН, F2=30 кН, F3=40 кН, F4=8 кН
1. -30,1кН
2. 46,5кН
3. -71,6кН
4. 103кН
13. Эквивалентными являются пары сил
1. а) Сила пары 100 кН, плечо 0,5 м
б) Сила пары 20 кН, плечо 2,5 м
2. а) М1= - 300 Н·м
б) М2= 300 Н·м
|
|
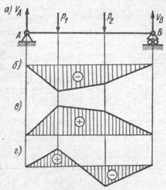
14. Выбрать нужные уравнения равновесия для определения реакций опор балки, изображенной на рисунке
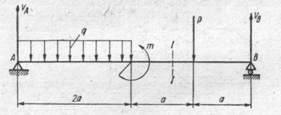
1. Уравнения равновесия: ∑ Fiy= 0; ∑ Mb= 0
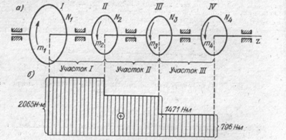
2. Уравнения равновесия: ∑ Mа = 0; ∑ Mb = 0
15. Значение величины равнодействующей силы, при Fx = 30H, Fy = 40H.
1. 25Н
2. 50Н
3. 70Н
16. Груз F находится в равновесии. Указать, какой из треугольников сил для шарнира В построен верно
1. 1
2. 2
3. 3
4. 4
17. Многоугольник сил, соответствующий уравновешенной системе сходящихся сил
 | |||||
 |  | ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
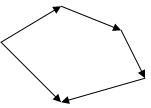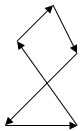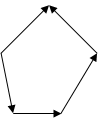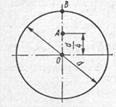
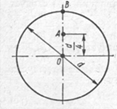
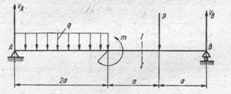
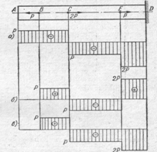
18. Пара сил изображена на рисунке
 | |||||||||
 | |||||||||
 | |||||||||
 |  | ||||||||
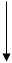1 2 3 4
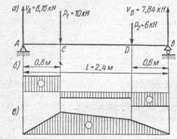
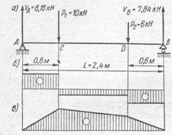
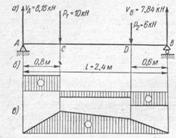
19. Чему равна проекция силы на ось Y
|
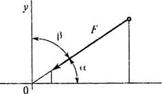
1. Fy=Fsinβ
2. Fy=Fcosβ
3. Fy= -Fsinβ
4. Fy= -Fcosβ
20. Выбрать формулу для расчета равнодействующей плоской системы сходящихся сил
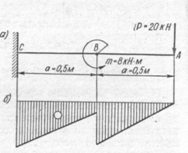
1. 
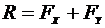
2. 
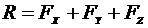
3. 
!
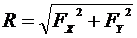4. 
21. Определить алгебраическую сумму моментов сил относительно точки А
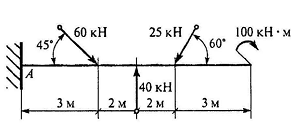
1. 0
2. 77,6 кН
3. 178,8кН
22. Выбрать наиболее подходящую систему уравнений равновесия для определения реакций в опорах изображенной балки
1. ΣFΧ=0; ΣFY=0; ΣMB=0
2. ΣFΧ=0; ΣFY=0; ΣMC=0
3. ΣFΧ=0; ΣMA=0; ΣMB=0
4. ΣFY=0; ΣMA=0; ΣMB=0277,6кН
23. Определить алгебраическую сумму моментов сил относительно точки В F=3кH, m=3кH·м, q=3кH/м; β=30°
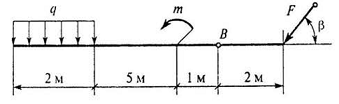
1. 36кН
2. 6кН
3. 30кН
4. 33кН
24. Тело находится в равновесии. m1==15Нм; m2 =8Нм; m3 =12Нм; Определить величину момента пары m4
1. 14Нм
2. 19Нм
3. 11Нм
4. 15Нм
25. Определить момент результирующей пары сил МΣ
|
|
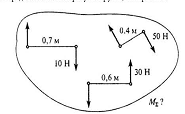
1. 5Нм
2. 9Нм
3. 31Нм
4. 45Нм
26. К двум материальным точкам массой 5 и 15 кг приложены одинаковые силы. Сравнить величины ускорений точек
1. Ускорения одинаковы
2. Ускорения точки массой 15 кг в три раза меньше
27. Две материальные точки движутся по прямой с постоянными скоростями 10 и 100 м/с. К этим точкам приложены эквивалентные силы
1. Да
2. Нет
28. Задачи динамики можно решать с помощью уравнений равновесия
1. Нельзя
2. Можно
29. Значения внутренних силовых факторов изменятся в зависимости от того, будут они вычислены по внешним силам, расположенным слева от сечения или справа от него
1. Да
2. Нет
30. Возможность определения траектории движения точки, если известно, как изменяются во времени координаты точки в прямоугольной системе координат(например, x=a·t2; y=b·t2)
1. Можно
2. Нельзя
31. Возможность определения пройденной пути по заданной траектории
1. Можно
2. Нельзя
32. Допускаемое напряжение при расчете на прочность было принято равным 180Н/мм2.После окончательного выбора размеров конструкции рабочее напряжение оказалось равным 185 Н/мм2.Угроза опасности разрушения для конструкции
1. Есть
2. Нет
33. Движение тела описывается уравнением S=0,25t2 +0,14t. Определите скорость тела через 2с после начала движения.
1. 10 м/с
2. 10,14м/с
3. 10,28 м/c
4. 0,39 м/c
34. Движение, при котором все точки тела описывают окружности вокруг общей неподвижной оси называются…Вращательным
35. Движение тела описывается уравнением S=0,25t2 +0,14t. Определить скорость тела через 2с после начала движения
1. 10 м/с
2. 10,14м/с
3. 10,28 м/c
4. 0,39 м/c
36. Движение твердого тела, при котором всякая прямая линия на теле при движении остается параллельной своему начальному положению называется…поступательным
|
|
37. Вычислить вращающий момент на выходном валу электродвигателя. Мощностьэлектродвигателя 2 кВт, частота вращения вала 750 об/мин.
1. 2,6Нм
2. 25,5Нм
3. 157Нм
4. 1500Нм
38. Изменение кинетической энергии прямолинейно движущейся точки, если скорость увеличится в два раза
1. Увеличится в два раза
2. Увеличится в четыре раза
39. Вычислить вращающий момент па валу электродвигателя при заданной мощности 7 кВт и угловой скорости 150 рад/с.
1. 5Нм
2. 46,7Нм
3. 1050Нм
4. 78Нм
40. Тело массой 5 кг движется по горизонтальной прямой. Сила трения равна 6Н. Определить коэффициент трения
1. 8,3
2. 0,83
3. 1,2
4. 0,12
41. При осевом растяжении и сжатии внутренние силы упругости в поперечном сечении могут быть заменены одной силой, направленной вдоль оси стержня-…… силой продольной
42. Чему равен коэффициент запаса прочности, если предельное напряжение 100 МПа, а расчетное напряжение 80 МПа?
1. 0,25
2. 0,2
3. 0,8
4. 1,25
43. Перевести в единицы системы СИ напряжение выраженное в 1600 кгс/см2
1. 16 Н/мм2
2. 160 Н/мм2
3. 16.3 Н/мм2
4. 163 Н/мм2
44. Перевести в единицы системы СИ напряжение выраженное в 16 кгс/мм2
1. 16 Н/мм2
2. 160 Н/мм2
3. 16.3 Н/мм2
4. 163 Н/мм2
45. Перевести в единицы системы СИ напряжение выраженное в 5000 кгс/см2
1. 50 Н/мм2
2. 500 Н/мм2
3. 51Н/мм2
4. 510 Н/мм2
46. Пользуясь методом сечений определить величину поперечной силы в сечении I-I
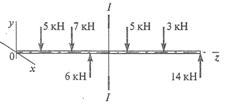
1. 2кН
2. 4кН
3. 6кН
4. 7кН
47. На брус круглого поперечного сечения диаметром 10 см действует продольная сила 314 кН. Рассчитать напряжение.
1. 4 МПа
2. 40 кПа
3. 40 МПа
4. 4 Па
48. Возможность определения закона распределения внутренних сил по сечению с помощью метода сечения
1. Можно
2. Нельзя
49. Через любую точку бруса можно провести различные сечения, например, перпендикулярно оси или под углом к ней. Определить изменение величины и направления напряжения в данной точке при изменении направления плоскости сечения
1. Изменится
2. Не изменится
50. Вычислить величину продольной силы, возникающей в поперечном сечении растянутого стержня, если нормальные напряжения в этом сечении равны 140 Н/мм2, а его площадь составляет 100 мм2
1. 0,71 Н
2. 1,4 Н
3. 14Н
4. 14000Н
51. Выбрать соответствующую эпюру продольных сил в поперечных сечениях бруса
+ - + - + - +
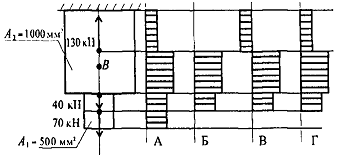
1. А
2. Б
3. В
4. Г
52. Образцы из стали и дерева с равной площадью поперечного сечения растягиваются одинаковыми силами. Сравнить возникающие в образцах напряжения
1. В стальном образце возникнут больше напряжений, чем в деревянном.
2. В образцах возникнут равные напряжения
53. Определить различие внутренних силовых факторов в поперечных сечениях, показанных на рисунке
1. Продольная сила для стержня на рисунке а, в два раза больше
2. Продольные силы одинаковы
54. 
Выбрать эпюру, соответствующую заданной нагрузке стержня
1. Эпюра, изображенная на рис. 1, а.
2. Эпюра, изображенная на рис. 1,б.
3. Эпюра, изображенная на рис. 1, в.
55. На рисунке изображена схема нагружения стержня и приведена соответствующая эпюра продольных сил. Определить по эпюре величину продольных сил на участке I
1. N=0кН
2. N=12кН
3. N=-12кН
56. На рисунке изображена схема нагружения стержня и приведена соответствующая эпюра продольных сил. Определить по эпюре величину продольных сил на участке II
1. N=-4кН
2. N=4кН
3. N=12кН
57. 
На рисунке изображена схема нагружения стержня и приведена соответствующая эпюра продольных сил. Определите по эпюре величину продольных сил на участке III
1. N=4кН
2. N=12кН
3. N=-12кН
58. На рисунке изображена схема нагружения стержня и приведена соответствующая эпюра продольных сил. Определите по эпюре величину продольных сил на участке IV
1. N=0кН
2. N=-8кН
3. N=8кН
59. Рабочее напряжение, возникающее в детали, равно σ=160 Н/мм2, а опасное (предельное) напряжение для материала детали σпред = 320 Н/мм2. Определить коэффициент запаса прочности.
1. S=0.44
2. S=2
3. S=0.2
60. Проставьте вместо знака 
соответствующий математический знак, чтобы не нарушалось условие прочности при растяжении и сжатии:
1. 
<
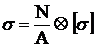2. >
3. ≥
4. ≤
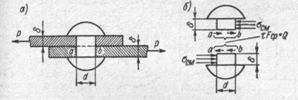
61. Выбрать точную запись условия прочности при растяжении и сжатии:
1. 
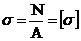
2. 
3. 
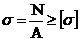
4. 
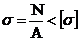
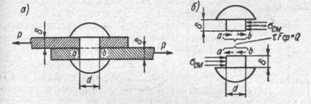
62. Полоса площадью поперечного сечения 50 мм3 растягивается силами 8000 Н, направленными вдоль ее оси. Вычислить нормальные напряжения
1. 
N=0,16
2. N=160
3. N=1600
63. Вычислить напряжения среза при d = 20 мм, Р= 60 кН
1. τ = 191 Н/мм2
2. τ = 300 Н/мм2
3. τ = 1200 Н/мм2
64. Вычислить напряжения смятия при δ = 16 мм, Р= 60 кН
1. σ = 187,5 Н/мм2
2. σ = 375 Н/мм2
3. σ = 960 Н/мм2
65. Диаметр заклепки увеличился в два раза. Изменение расчетного напряжения среза
1. Уменьшится в два раза
2. Уменьшится в четыре раза
66. Кратность изменения допускаемой нагрузки на сварное соединение, при уменьшении толщины шва вдвое (при прочих равных условиях)
1. Уменьшится в четыре раза
2. Уменьшится вдвое
67. Справедливость закона Гука при кручении, если напряжение не превышает предела пропорциональности материала при кручении
1. Справедлив
2. Не справедлив
68. Зависимость величины рабочих (расчетных) касательных напряжений от материала вала
1. Зависит
2. Не зависит
69. Зависимость угла поворота сечения вала от материала, из которого он изготовлен
1. Зависит
2. Не зависит
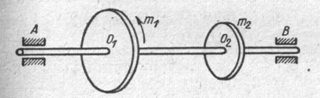
70. Вал вращается равномерно, вращающий момент на ведущем шкиве т1 = 5000 Н·м. Определить величину момента т2 на ведомом шкиве.
1. 2500
2. 5000
3. 10000
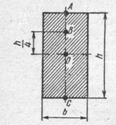
71. Указать, для какой точки на рисунке поперечного сечения балки нормальные напряжения могут быть вычислены по формуле σ= 
1. Для точки О
2. Для точки В
3. Для точек А и С
72. 
Точка поперечного сечения балки, на которой возникает наибольшие нормальные напряжения
1. Точка А
2. Точка О
3. Точка В
73. Возможность появления скачков на эпюре изгибающих моментов, при нагружении балки сосредоточенными силами ираспределенной нагрузкой
1. Могут
2. Не могут
74. Возможность зависимости величины нормальных напряжений от форм поперечных сечений балки
1. Зависят
2. Не зависят
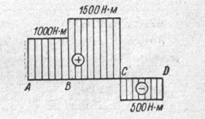
75. На рисунке показана эпюра крутящих моментов. Определить величину максимального крутящего момента, по которому нужно рассчитывать вал на прочность
1. 2000 Н ∙ м
2. 1500 Н ∙ м
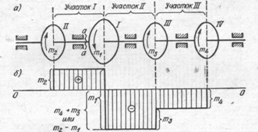
76. Указать рисунок, на котором более рациональное расположение ведущего шкива
1. На рисунке 1
2. На рисунке 2
77. Вычислить полярный момент сопротивления сечения круглого сплошного вала d = 30 мм
1. 177
2. 2649
3. 5300
78. Указать, для какой точки поперечного сечения на рисунке можно вычислить напряжения по формуле 
1. Для точки А
2. Для точки В
3. Для точки О
79. Допускаемое напряжение при расчете на прочность было принято равным 180Н/мм2.После окончательного выбора размеров конструкции рабочее напряжение оказалось равным 185 Н/мм2.Угроза опасности разрушения для конструкции
1. Есть
2. Нет
80. Кратность уменьшения напряжения в точке А кнапряжению в точке В
1. В четыре раза
2. В два раза
81. Изменение величины максимального напряжения вала в поперечных сечениях, если диаметр вала увеличить в два раза
1. Уменьшится в два раза
2. Уменьшится в четыре раза
3. Уменьшится в восемь раз
82. 
Указать уравнение, в котором есть ошибка
1. ∑ МА= 0; q·2a ∙ a + P ∙ 3a – VB ∙ 4a = 0;
2. ∑ МB= 0; -P·a - q∙ 2a ∙ 3a + VA∙ 4a = 0;
3. ∑ Pi = 0; VA - P - q∙2a +VB = 0;
83. 
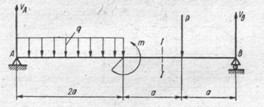Указать силы, приложенные к балке, которыевызывают положительную поперечную силу в сечении I - I:
1. Силы Va, Р
2. Нагрузки q, m
3. Сила Vb
84. Зависимость величины критической силы от упругих свойств материала стержня
1. Зависит
2. Не зависит
85. Зависимость прочности материала от характера изменения напряжений во времени
1. Зависит
2. Не зависит
86. Возможность разрушения детали, при работе ее при переменных напряжениях, которые меньше предела текучести
1. Не может
2. Может
87. Возможность влияния формы детали на ее предел выносливости
1. Влияет
2. Не влияет
88. 
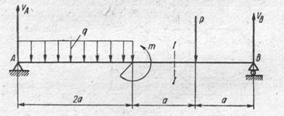Указать силы, приложенные к балке, которые вызывают положительный изгибающий момент в сечении I – I
1. Сила Р
2. Силы VА, VB
89. На рисункеизображена балка, нагруженная сосредоточенными силами, приведены эпюры поперечных сил и изгибающих моментов. Вычислить величину ординатыQ этих эпюр в характерном сечении А
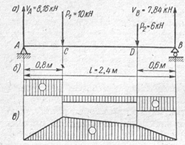
1. -1,84
2. -8,16
3. 1,84
4. 8,16
90. На рисункеизображена балка, нагруженная сосредоточенными силами, приведены эпюры поперечных сил и изгибающих моментов. Вычислить величину ординаты Q этих эпюр в характерном сечении С
1. -1,84
2. 1,84
3. -10
4. 10
91. На рисункеизображена балка, нагруженная сосредоточенными силами, приведены эпюры поперечных сил и изгибающих моментов. Вычислить величину ординаты Q этих эпюр в характерном сечении Д
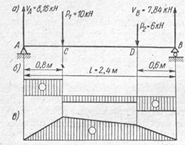
1. -1,84
2. 1,84
3. -7,84
4. 7,84
92. На рисункеизображена балка, нагруженная сосредоточенными силами, приведены эпюры поперечных сил и изгибающих моментов. Вычислить величину ординаты MА этих эпюр в характерном сечении А
1. 0
2. 1,49
3. 8.16
93. На рисункеизображена балка, нагруженная сосредоточенными силами, приведены эпюры поперечных сил и изгибающих моментов. Вычислить величину ординаты MС этих эпюр в характерном сечении С
1. -6,53
2. 6,53
3. -8,16
4. 8,16
94. На рисункеизображена балка, нагруженная сосредоточенными силами, приведены эпюры поперечных сил и изгибающих моментов. Вычислить величину ординаты MД этих эпюр в характерном сечении Д
1. -4,71
2. 4,71
3. -6
4. 6
95. На рисункеизображена балка, нагруженная сосредоточенными силами, приведены эпюры поперечных сил и изгибающих моментов. Вычислить величину ординаты MВ этих эпюр в характерном сечении В
1. 0
2. -7,84
3. 7,84
96. На рисункеизображена консольная балка, нагруженная сосредоточенной силой Р и парой сил, момент которой равен m. Вычислить величину изгибающих моментов в сечении А
1. 0
2. -20
3. 20
97. 
На рисункеизображена консольная балка, нагруженная сосредоточенной силой Р и парой сил, момент которой равен m. Вычислить величину изгибающих моментов в сечении В справа
1. -8
2. 8
3. -10
4. 10
98. 
На рисункеизображена консольная балка, нагруженная сосредоточенной силой Р и парой сил, момент которой равен m. Вычислить величину изгибающих моментов в сечении В слева
1. -2
2. 2
3. -8
4. 8
99. На рисункеизображена консольная балка, нагруженная сосредоточенной силой Р и парой сил, момент которой равен m. Вычислить величину изгибающих моментов в сечении С
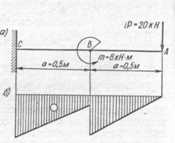
1. -10
2. 10
3. -12
4. 12
100. 
На рисункеизображена консольная балка, нагруженная сосредоточенной силой Р и парой сил, момент которой равен m. Определить величину скачка на эпюре изгибающих моментов в сечении В
1. 8
2. 10
3. 12
101. На рисункеизображена балка, нагруженная сосредоточенными силами. Определить, какая из приведенных на рисунке эпюр изгибающих моментов соответствует нагружению балки
1. Рисунок б
2. Рисунок в
3. Рисунок г
102. Изменение величины и знака поперечной силы и изгибающего момента, при вычислении их по внешним силам, расположенным слева или справа от сечения
1. Изменяются
2. Не изменяются
103. Вычислить эквивалентный момент по третьей теории прочности. Изгибающий момент в поперечном сечении вала Ми = 4000 Н∙м. Крутящий момент в том же сечении Мк = 3000 Н∙м
1. 2500
2. 5000
3. 7000
104. Изменение величины критической силы, при увеличении длины стержня в два раза
1. Уменьшится в два раза
2. Уменьшится в четыре раза
3. Уменьшится в восемь раз
105. Изменение величины критической силы, при замене шарнирных опор стержня опорами с жестким защемлением
1. Увеличится в четыре раза
2. Уменьшится в четыре раза
106. Вычислить гибкость стержня круглого поперечного сечения диаметром d= 4 см. Длина стержня l = 120 см, концы закреплены шарнирно
1. λ = 30
2. λ = 120
3. λ = 3600
107. По заданному изгибающему моменту при одинаковых допускаемых напряжениях были подобраны прямоугольные сечения балок в трех вариантах с разными соотношениями высоты h и ширины b: вариант I - h:b = 2; вариант II - h: b = 3; вариант III - h: b = 2,5. Указать вариант балки, которая будет иметь наименьшую массу
1. С наименьшей высотой
2. С наибольшей высотой
108. Кратность уменьшения нормальных напряжений в прямоугольном сечении балки, при увеличении ее высоты в два раза
1. В два раза
2. В четыре раза
3. В восемь раз
109. Изменение прогиба балки, при уменьшении изгибающего момента в три раза
1. Уменьшится в три раза
2. Увеличится в три раза
3. Уменьшится в девять раз
110. Назначение шайбы
1. предохранение от задиров
2. увеличение опорной поверхности
3. облегчение затягивания
111. Определить величину скорости точки, если заданы проекции скорости на оси координат: Vx=3м/с,Vy=4м/с
1. 5
2. 7
3. 12
112. В зависимости от принципа действия все механические передачи делят на группы
1. с зацеплением
2. с проскальзыванием
3. с трением
113. Соединения, при разборке которых нарушается целостность составных частей изделия…
114. Определить передаточное число передачи, если Z1=25, Z2=50
1. u =2
2. u =0,5
115. Основные критерии работоспособности машин
1. прочность
2. жесткость
3. устойчивость
116. В зависимости от формы профиля различают типы резьб
1. треугольные
2. круглые
3. квадратные
117. Проверочные расчеты валов выполняются
1. на жесткость
2. на износостойкость
3. на усталость
118. Основными критериями работоспособности подшипников качения являются
1. прочность
2. износостойкость
3. долговечность
119. Шлицевые соединения различают по форме зубьев
1. эвольвентные
2. треугольные
3. сегментные
120. К передачам зацеплением относятся
1. цепные
2. фрикционные
3. зубчатые
121. К приводным цепям относятся:
1. круглозвенные цепи
2. зубчатые
3. втулочные
122. Достоинства подшипников скольжения
1. большие габариты
2. большая долговечность
3. восприимчивость к ударным нагрузкам
123. Галтель на валах необходима
1. для повышения прочности
2. для установки деталей
3. для уменьшения концентрации напряжения
124. Основные типы резьб
1. метрическая
2. дюймовая
3. цилиндрическая
125. К передачам гибкой связью относятся
1. фрикционные
2. цепные
3. ременные
126. Постоянные муфты
1. Втулочные
2. Фрикционные
3. Обгонные
127. Стандартные муфты подбирают
1. в зависимости от диаметра
2. в зависимости от мощности
3. в зависимости от вращающего момента
128. Назначение шайбы
1. предохранение от задиров
2. увеличение опорной поверхности
3. облегчение затягивания
129. В зависимости от формы поверхности, на которой образуется резьба различают
1. цилиндрические
2. фасонные
3. конические
130. По форме тел качения подшипники делятся
1. шариковые
2. тарированные
3. игольчатые
131. Передача, служащая для передачи вращательного движения от одного вала к другому с помощью сил трения, прижатыми друг другу дисками, цилиндрами или конусами…
132. В шевронной передаче уравновешиваются … силы
133. Муфта, передающая вращающий момент только в одном направлении …
134. Соединения, разработка которых происходит без нарушения целостности составных частей изделия…
135. Определить передаточное отношение передачи, если ω1=50 рад/с, ω2=100 рад/с.
1. u=2
2. u=1/2
136. Детали, с помощью которых за счет приводного ремня передается вращательное движение - …
137. Бесступенчатое регулирование передаточного отношения возможно в … передаче
138. Определить передаточное отношение передачи, если n1=100 об/мин, n2=50 об/мин.
1. u=2
2. u=1/2
139. Механизмы, передающие энергию двигателя исполнительному органу машины…
140. Частота вращения ведущего звена n1=1000 об/мин, передаточное отношение u=4. Определить частоту вращения ведомого вала
1. n2=250 об/мин
2. n2=4000 об/мин
141. Для соединения соосных валов применяются …
142. Детали с помощью которых за счет цепи передается вращательное движение…
143. Определить диаметр подшипника 208
144. Определить диаметр подшипника 7312
145. Определить диаметр подшипника 36210
146. Определить модуль зубьев, если шаг Р = 7 мм
1. 2,2
2. 22