6. Картограмма. Для построения картограммы необходима географическая карта с четко обозначенными контурами границ административных территорий, которые заштриховываются с различной интенсивностью соответственно уровню интенсивного показателя (Рис.6).
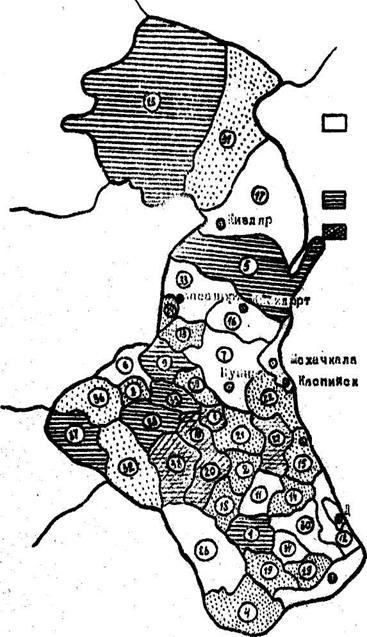
до 10 врачей

Врачей
16-20 врачей
св. 20 врачей
Избербаш
Дербент
Рис. 6. Обеспеченность врачами населения Республики Дагестан (на 10000 населения).
7. Картодиаграмма. Картодиаграмма представляет собой сочетание географической карты с диаграммой, чаще всего столбиковой, причем столбики различной величины (соответственно показателю) наносятся на карту и ставятся на той территории, которую они представляют.
Примерный перечень задач для самостоятельной работы
Задача 1. Структура причин смертности в России
| Причины смерти | Процент к итогу |
| Внематочная беременность Искусственный медицинский аборт Аборты, начатые вне лечебного учреждения Кровотечения Токсикоз беременности Сепсис во время родов и после родового периода Другие осложнения беременности, родов и послеродового периода | 8,3 2,1 22,6 13,5 14,8 3,0 35,7 |
| ИТОГО: | 100,0 |
На основании приведенных данных построить соответствующий вид диаграммы.
Задача 2. Младенческая смертность в России в 1990-1994 г.г. /на 1000 родившихся/ составила:
1990 г. – 17,4
1991 - 17,8
1992 - 18,0
1993 - 24,0
1994 - 18,6
На основании приведенных данных построить соответствующий вид диаграммы.
Задача 3. Изобразите графически распределение числа заболеваний дизентерией по месяцам года в абсолютных цифрах в Хивском районе:
| Месяцы | Количество заболеваний | Месяцы | Количество заболеваний |
| Январь | Июль | ||
| Февраль | Август | ||
| Март | Сентябрь | ||
| Апрель | Октябрь | ||
| Май | Ноябрь | ||
| Июнь | Декабрь | ||
| ИТОГО: 220 |
Задача 4. Частота болезней органов дыхания по РФ на 1000 населения составляла:
Среди взрослого населения - 214,5
подростков - 376,7
детей - 709,3.
На основании приведенных данных построить соответствующий вид диаграммы.
Задача 5. Распределение женщин-врачей Дагестана по специальностям
| Специальность | Процент к итогу |
| Педиатры Терапевты Акушеры-гинекологи Врачи сан.-эпиднадзора Прочие | 23,6 21,4 12,3 12,1 30,6 |
| ИТОГО: | 100,0 |
На основании приведенных данных построить соответствующий вид диаграммы.
Задача 6. Общая заболеваемость врачей-мужчин Дагестана /на 1000 врачей/ составила: 1157,1; врачей-женщин – 3012,4. Изобразить эти данные графически, выбрав соответствующий вид диаграммы.
Задача 7. Структура причин детской смертности в Дагестане
| Причины смерти | Процент к итогу |
| Болезни перинатального периода Врожденные пороки развития Болезни органов дыхания Инфекционные и паразитарные болезни Травмы и отравления Прочие | 44,5 21,4 14,5 6,6 4,7 8,3 |
| ИТОГО: | 100,0 |
На основании приведенных данных построить соответствующий вид диаграммы.
Задача 8. Изобразите графически локализацию повреждений кожи у рабочих предприятий.
| Локализация повреждений | Процент к итогу |
| Ладонные и боковые поверхности пальцев Ладонь Тыл кисти и пальцев Предплечье Лицо, шея | 49,2 11,7 30,2 7,0 1,9 |
| ИТОГО: | 100,0 |
Задача 9. Показатели рождаемости в России /на 1000 человек/ по годам составляла:
1990 - 13,4
1991 - 12,1
1992 - 10,7
1993 - 9,4
1994 - 7,7
Построить соответствующий вид диаграммы.
Контрольные вопросы
1. Для чего применяют графическое изображение?
2. Какие виды диаграмм применяются в санитарной статистике?
3. Когда применяют линейные диаграммы и какие правила построения линейных диаграмм?
4. Какие диаграммы применяются для изображения интенсивных и экстенсивных показателей?
5. Как строится радиальная диаграмма?
6. Как строится секторная диаграмма?
Средние величины
Для обобщения численных выражений, которыми характеризуется какое – либо явление и свойственные им закономерности, применяются средние величины.
Средние величины применяются:
1. Для характеристики физического развития населения (основные антропометрические измерения, динамометрия, спирометрия и др.)
2. Для характеристики качественных показателей деятельности служб здравоохранения (средняя занятость койки в году, среднее пребывание больного на койке, число посещений на одного жителя, средние сроки лечения и др.).
3. Для характеристики сан. – эпид. работы, санитарных условий местности, заселенности, среднее число жильцов в квартире, среднее количество квадратных метров на 1 человека и др.
4. В экспериментально - лабораторных исследованиях для характеристики физиологических сдвигов (температуры, числа дыхательных движений,числа сердечных сокращений, уровня артериального давления и др.).
Средняя величина определенного признака (рост, вес, окружность грудной клетки, возраст и т.д.) вычисляется из вариационного ряда, т.е. из ряда чисел, характеризующих этот признак, и отличающихся друг от друга своей величиной. Каждое числовое выражение варьирующего признака называется вариантной (V). Каждой варианте соответствует та или иная частота (р), т.е. число, указывающее как часто данный признак повторяется.
Данные исследования представляются в виде ряда вариант последовательно возрастающих или убывающих с соответствующими им частотами, которые нарастают к середине ряда.
Пример:
| Вес в кг. (V) | Частота признака (Р) |
| n = 51 |
Общее число случаев наблюдений из которых вариационный ряд состоит, обозначают буквой «n».
Из вариационного ряда определяется средний уровень изучаемого количественного признака, например: среднее время задержки дыхания, средний рост или вес групп и. т. д..
Средний уровень измеряют с помощью критериев, которые называются средними величинами. Под средней величиной понимают число, выражающее общую меру исследуемого признака в совокупности.
В здравоохранении чаще всего применяются три вида средних величин: мода (Мо), медиана (Ме) и средняя арефметическая (М).
Мода (Мо) – это величина признака, которая чаще других встречается в данной совокупности. В приведенном примере Мо = 22 кг.
Медиана (Ме) - это величина признака, занимающая среднее положение в вариационном ряду, она делит ряд на две равные части. В примере Ме=22 кг (совпадение с Мо).
Для вариационного ряда может быть дана сводная характеристика в виде одной величины, называемой средней арифметической, которая при достаточном числе наблюдений отражает основную закономерность изучаемого явления.
Основными способами расчета средних величин являются: средне-арифметический способ и способ моментов. Среднеарифметический способ применяется для вычисления среднеарифметической простой и средне-арифметической взвешеной.
Среднеарифметическая простая (Мпр) вычисляется из вариационного ряда, в котором число наблюдений небольшое (n < 30), частота всех вариант р=1 и выражается формулой: М=∑V/n, т.е. сумма всех вариант, деленная на число наблюдений.
Пример:
| Вес в кг. (V) | Частота (Р) |
| n= 6 |
Мпр =  =
= 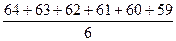 =
= 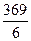 = 61,5 (кг).
= 61,5 (кг).
Среднеарифметическая взвешенная вычисляется из вариационного ряда, в котором число наблюдений небольшое (n < 30) и частота вариант р > 1.
М взв. = ∑VР/n, т.е. сумма произведений вариант на их частоту и деленная на число наблюдений.
Пример:
Масса тела 25 юношей в возрасте 18 лет.
| Вес в кг. (V) | Частота (Р) | VP |
| N= 25 | ∑VР =1540 |
М взв = 1540/25 = 61,6 кг.
Среднеарифметическая по способу моментов – это способ применяется тогда, когда вариационный ряд состоит из большого количества наблюдений (n > 30), а варианты – из многочисленных чисел.
Методика вычисления средней арифметической по способу моментов заключается в следующем: варианта вариационного ряда, имеющая наибольшую частоту (Мо) принимается за условную среднюю, обозначаемую М1. Затем определяется отклонение каждой из вариант от этой условной средней по формуле: d= V – M1.
Среднее отклонение членов данного вариационнного ряда от условной средней будет иметь выражение ∑dp / n. Называется это среднее отклонение - моментом первой степени.
Таким образом, средняя арифметическая, вычисленная по способу моментов, равна условно взятой средней величины (М1) плюс среднее отклонение от нее всех членов ряда ∑dp/n, т.е. М = М1 + 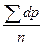 .
.
Пример вычисления средней арифметической по способу моментов.
Вычислить средний возраст врачей психиатров по способу моментов по следующим данным:
| Возрасть в годах. (V) | Частота (Р) | d (V – M1) | dp |
| 22,5 | - 15 | ||
| 27,5 | - 10 | - 80 | |
| 32,5 | -5 | -30 | |
| 37,5 | |||
| 42,5 | |||
| 47,5 | |||
| 52,5 | |||
| 57,5 | |||
| 62,5 | |||
| n= 51 | ∑dp= +75 |
М1 = М0 = 37,5г.
∑dp / n = +75/51 = 1,5г. (условное среднее отклонение или момент первой степени)
М = 37,5 + 1,5 = 39,0 года.