Задача 1. Имеются следующие результаты рабочих за смену:
| Табельные номера рабочих | ||||||||||
| Количество изготовленных деталей |
Вычислить: 1) среднюю выработку одного рабочего; 2) среднее линейное отклонение; 3) дисперсию; 4) коэффициент вариации.
1) Средняя выработка на одного рабочего может быть вычислена, как средняя арифметическая простая:
где 
– количество изготовленных деталей, п =_____ – общее число рабочих.
2) Среднее линейное отклонение вычисляется, как среднее арифметическое из абсолютных значений отклонений отдельных вариант от их среднего арифметического:
.
Составим вспомогательную таблицу для промежуточных расчётов:
Количество изготовленных деталей ( )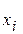
| ||||||||||
| ||||||||||
|
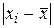
Тогда:
3) Будем вычислять дисперсию, как 
. Составим ещё одну вспомогательную таблицу:
| Количество изготовленных деталей ()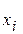
| ||||||||||
|
Тогда 
и дисперсия 
4) Коэффициент вариации вычисляется, как отношение среднего квадратического отклонения к среднему ожидаемому значению и показывает степень отклонения получаемых результатов: 
.
Среднее квадратическое отклонение находим, как корень квадратный из дисперсии: 
И искомый коэффициент вариации: 
Задача 2. В фирме работают ____ бригад. Численность рабочих отдельных бригад составляет соответственно __________________________________ человек. Определите медиану численности рабочих в бригаде.
Решение. Составим ранжированный дискретный ряд. Наращивание суммы частот продолжаем до получения накопленной суммы частот, превышающей половину суммы частот ряда.
| Численность рабочих в бригаде | Частота 
| Сумма накопленных частот |
| ||
| ||
| ||
| ||
| ||
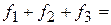
| Итого |
В третьем столбце ненужное – зачеркнуть, а при необходимости – продолжить подсчёты.
В нашем примере сумма частот составила _______, её половина – ______. Накопленная сумма частот получилась равной ____. Варианта, соответствующая этой сумме, и есть медиана ряда: 
__________
Задача 3. Имеются следующие данные о средней часовой заработной плате (руб.) десяти рабочих: __________________________________________________________. Определить медиану средней часовой заработной платы рабочих.
Решение. Составим ранжированный дискретный ряд. Наращивание суммы частот продолжаем до получения накопленной суммы частот, превышающей половину суммы частот ряда.
| Средняя часовая заработная плата (руб.) | Частота
| Сумма накопленных частот |
| 1
| ||
| 3
| ||
| 4
| ||
| 5
| ||
|
| ||
| Итого |
В третьем столбце ненужное – зачеркнуть, а при необходимости – продолжить подсчёты.
В данном примере сумма накопленных частот против одной из вариант равна точно половине суммы частот ряда, поэтому медиана определяется как средняя арифметическая этой варианты и последующей: 
Задача 4. Результаты сдачи экзамена по теории вероятностей в одной группе характеризуются следующими данными:
| Оценка: | ||||
| Число студентов: |
Найдите модальный балл успеваемости студентов группы.
Решение. Для дискретных вариационных рядов модой является значение варианты с наибольшей частотой. Поэтому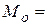 
_______
Задача 5. Имеются данные об урожайности пшеницы в центнерах с 1 га:
| Урожайность (цент. с 1 га) | Посевная площадь (га) |
Определить: 1) среднюю урожайность пшеницы способом моментов; 2) среднее линейное отклонение; 3) моду и медиану; 4) показать моду и медиану на гистограмме.
Решение. 1) Для вычисления среднего значения используем метод моментов. Составим вспомогательную таблицу, куда будем заносить:
- середины заданных интервалов, определяемые, как полусуммы от их границ: 
, где 
и 
- левая и правая граница i -го интервала соответственно;
- значения 
отклонений от условного нуля, за который принимаем моду 
дискретного ряда, составленного из середин интервалов;
- условные значения вариант, вычисляемые, как их отклонения от условного нуля, делённые на шаг h, вычисляемый, как разность между правой и левой границей интервала:
h = ________.
Метод моментов используется только в рядах с равными интервалами, у которых длина шага постоянна!
Урожайность 
(цент. с 1 га)
| Посевная площадь
(га)
| середины интервалов
| отклонения от условного нуля
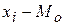
| условные значения вариант
|
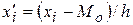
| Итого |
Средняя арифметическая взвешенная для условных вариант будет равна:
Окончательно среднюю урожайность пшеницы находим, умножив полученный результат на шаг h и прибавив моду 
:
2) Среднее линейное отклонение вычисляется, как среднее арифметическое из абсолютных значений отклонений отдельных вариант от их среднего арифметического:
.
Составим вспомогательную таблицу для промежуточных расчётов:
| Урожайность
(цент. с 1 га)
| Посевная площадь
(га)
| середины интервалов
| отклонения вариант от среднего арифметического
| абсолютные значения отклонений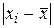
|
| Итого |
Тогда:
3) Мода интервального ряда определяется следующим образом:
- по максимальному значению частоты находим модальный интервал (тот, в котором расположено значение моды): 
________________;
- внутри модального интервала находим значения:
________ – нижняя граница модального интервала;
________ – величина модального интервала;
________ – частота модального интервала;
________ – частота интервала, предшествующего модальному;
________ – частота интервала, следующего за модальным.
- значение моды вычисляем по формуле:
Вычисляем медиану 
интервального ряда. Для этого:
- по накопленным частотам находим медианный интервал, который характеризуется тем, что его накопленная частота равна или превышает половину суммы всех частот ряда:
________________;
- внутри медианного интервала находим значения:
________ – нижняя граница медианного интервала;
________ – величина медианного интервала;
________ – частота медианного интервала.
∑ fi = ______________________________________________________ – сумма частот;
= __________________________________________________– сумма накопленных частот, предшествующих медианному интервалу;
- значение медианывычисляем по формуле:
=
4) Строим гистограмму, демонстрирующую распределение урожайности пшеницы по посевной площади и отмечаем на ней моду и медиану.
 |
Задача 6. Распределение рабочих по общему стажу работы составило:
| Стаж работы (лет) | Число рабочих | |
| 1 цех | 2 цех | |
| Итого: |
Вычислите: 1) среднюю из групповых дисперсий; 2) межгрупповую дисперсию; 3) общую дисперсию, используя правило сложения дисперсий.
Решение. Будем находить дисперсию двумя способами.Для упрощения расчётов построим вспомогательные таблицы, куда занесём середины интервалов, соответствующих стажу работы, их квадраты и прочие результаты промежуточных вычислений.
| Стаж работы (лет)
| середины интервалов
| 
| Число рабочих | 
| 
| 
| 
| |
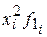
1 цех
( )
| 2 цех
( )
| |||||||
| Итого: | 
| 
| ||||||
| Групповые средние | 
| 
|
| Стаж работы (лет)
| середины интервалов
| Число рабочих | 
| 
| 
| 
| |
1 цех
( )
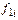| 2 цех
( )
| ||||||
| Итого: |
|
|
1) Рассчитаем групповые дисперсии. Очевидно, что сначала нам нужно найти средние арифметические по двум группам (обратите внимание, значения сумм у нас уже есть, в таблице!):
Тогда дисперсия для первой группы:
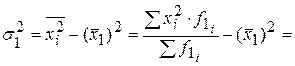
или 
Как видим, результаты совпали.
Дисперсия для второй группы:
или 
Результаты совпали.
Средняя из групповых дисперсий рассчитывается, как
2) Межгрупповую дисперсию найдём по формуле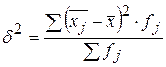 
,
где 
Тогда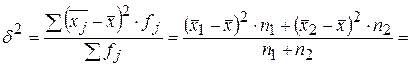 
3) Общую дисперсию вычислим, используя правило сложения дисперсий:
