Формулировка теорем. И определения
Теорема о Ранге Матрицы.
Ранг матрицы равен максимальному числу линейно независимых строк этой матрицы.
В самом деле, пусть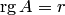 
. Тогда в матрице 
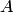имеется 
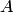линейно независимых строк. Это строки, в которых расположен базисный минор. Если бы они были линейно зависимы, то этот минор был бы равен нулю по теореме 3.2, а ранг матрицы не равнялся бы . Покажем, что — максимальное число линейно независимых строк, т.е. любые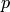 
строк линейно зависимы при 
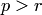. Действительно, образуем из этих 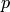строк матрицу 
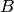. Поскольку матрица 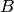— это часть матрицы 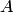, то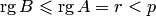 
. Значит, хотя бы одна строка матрицы 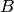не входит в базисный минор этой матрицы. Тогда по теореме о базисном миноре она равна линейной комбинации строк, в которых расположен базисный минор. Следовательно, строки матрицы 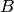линейно зависимы. Таким образом, в матрице 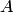не более, чем линейно независимых строк.
Следствия
Следствие 1. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов:
Следствие 2. При элементарных преобразованиях строк матрицы линейная зависимость (или линейная независимость) любой системы столбцов этой матрицы сохраняется.
Теорема о базисном миноре
Столбцы матрицы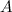 
, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы 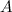линейно выражается через остальные столбцы из базисного минора.
В матрице 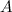размеров 
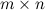минор 
-го порядка называется базисным, если он отличен от нуля, а все миноры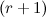 
-ro порядка равны нулю или их вообще не существует.
Следствие. Если все столбцы матрицы 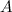линейно выражаются через столбцов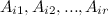 
, которые образуют линейно независимую систему, то ранг матрицы 
.
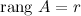Теорема Крамера
Если определитель матрицы отличен от нуля, то мы можем найти значения неизвестных переменных, заменяя столбец с неизвестными на столбец свободных членов.
Далее пользуемся формулой;
Определитель, который заменяля делим на определитель матрицы, это и будет ответ.
Теорема Кронекера- Капели
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. rangA=rangA˜.
Следствие из теоремы Кронекера-Капелли
Если rangA≠rangA˜, то СЛАУ несовместна (не имеет решений).
Если rangA=rangA˜<n, то СЛАУ является неопределённой (имеет бесконечное количество решений).
Если rangA=rangA˜=n, то СЛАУ является определённой (имеет ровно одно решение).
Общее решение однородной СЛАУ
Это когда вместо свободных переменных, мы ставим поочердно 0 и 1, и вычисляем неизвестные переменные.
Структура общего решения неоднородной СЛАУ
Свободные переменные равны 0, а в правой части остаются свободные члены.
Пример СЛАУ
А11x1+a12x2=b1
A21x1+a22x2=b2
Общий вид
Изменение координат вектора при изменении базиса
Пусть в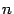 
-мерном линейном пространстве 
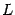выбран базис 
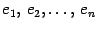, который мы будем для удобства называть "старый" и другой базис 
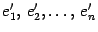, который мы будем называть "новый". Возьмем призвольный вектор 
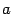из 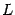. Его координатный столбец в старом базисе обозначим 
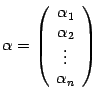, а в новом -- 
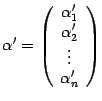. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису
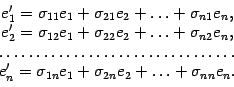
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса
Эта матрица называется матрицей перехода от старого базиса к новому.
Замечание 18.1 Матрица перехода всегда невырождена, то есть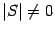 
.
Предложение 18.5 Координатные столбцы в старом базисе и в новом базисе связаны формулой
|
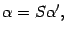