Основные определения.
· Вектор (геометрический вектор) — это направленный отрезок (отрезок, у которого одна граничная точка считается начальной, другая – конечной).
На чертеже вектор обозначается стрелкой
над буквенным обозначением вектора также ставится стрелка 
.
Вектор, фигурирующий в определении, носит название связанного, или закрепленного вектора.
· Закрепленный вектор 
— это направленный отрезок АВ, началом которого является точка А, а концом — точка В.
Свободный вектор — это множество всех закрепленных векторов, получающихся из фиксированного закрепленного вектора с помощью параллельного переноса. Обозначается 
.
Если же точка приложения вектора (точка A для вектора ) может быть выбрана произвольно, вектор называется свободным.
Если точка приложения может двигаться по линии действия вектора, говорят о скользящем векторе. Иначе говоря, свободный вектор является представителем бесконечного множества связанных или скользящих векторов.
· Нулевой вектор — это вектор, у которого начало и конец совпадают: 
· Коллинеарные векторы — это векторы, которые лежат на одной прямой, либо на параллельных прямых.
Нулевой вектор коллинеарен любому вектору.
· Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов, то эти векторы компланарны.
· Длина вектора (модуль) — это расстояние между началом и концом вектора. Обозначение: 
или 
· Два вектора равны, если они коллинеарны, имеют одинаковую длину и направление. Например, 
Алгебраические операции над векторами.
· Операция сложения.
Суммой двух свободных векторов и 
называется свободный вектор 
, начало которого совпадает с началом первого, а конец — с концом второго, если совмещены конец вектора и начало вектора .
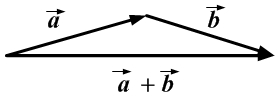
Сумма двух векторов и (
) — это вектор, идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора (правило треугольника).
Свойства операции сложения векторов:
1) Переместительное свойство: 
(коммутативность).
2) Сочетательное свойство: 
(ассоциативность).
3) Существует нулевой вектор 
, такой, что 
для любого вектора (особая роль нулевого вектора).
Нулевой вектор порождается нулевым закрепленным вектором, то есть точкой.
4) Для каждого вектора существует противоположный ему вектор 
, такой, что 
. Вектор 
называется вектором, противоположным вектору .
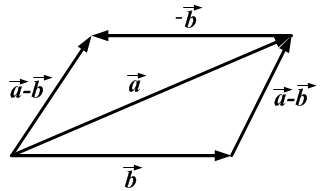
Правило параллелограмма (правило сложения векторов): если векторы и приложены к общему началу и на них построен параллелограмм, то сумма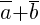 
этих векторов представляет собой диагональ параллелограмма, идущую из общего начала векторов и
Вычитание векторов определяется через сложение: 
.
Другими словами, если векторы и приложены к общему началу, то разностью векторов и будет вектор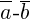 
, идущий из конца вектора к концу вектора .
|
|
· Операция умножения вектора на число.
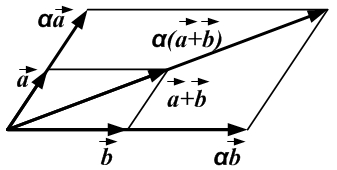
Произведением вектора на число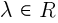 
называется вектор 
такой, что:
1) если λ > 0, ≠ , то 
получается из растяжением в λ раз: 
;
2) если λ < 0, ≠ , то получается из растяжением в | λ | раз и последующим отражением: 
;
3) если λ = 0 или 
, то 
.
Свойства операции умножения:
1) Распределительное свойство относительно суммы чисел: 
для любых действительных 
и всех (дистрибутивность).
2) Распределительное свойство относительно суммы векторов: 
(дистрибутивность).
3) Сочетательное свойство числовых сомножителей: 
(ассоциативность).
4) Существование единицы: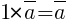 
.