1. Сформулировать обобщенную по Галеркину постановку первой краевой задачи для одномерного уравнения Пуассона.
2. Выписать аппроксимацию непрерывной на отрезке [0,1] функции 
в виде разложения по системе базисных функций-«крышек». Доказать, что результатом аппроксимации является ломаная линия, проведенная через значения функции в узловых точках.
3. Выписать систему линейных уравнений для значений неизвестной функции в узловых точках, полученную при аппроксимации обобщенного решения первой краевой задачи для одномерного уравнения Пуассона по методу Бубнова-Галеркина с использованием базисных функций-«крышек».
4. Дать определение линейного одномерного конечного элемента. Чем отличаются функции формы элемента от базисных функций-«крышек»?
5. Для линейного одномерного конечного элемента дать определение вектора нагрузки и матрицы жесткости. Выписать для них формулы в случае равномерной сетки.
6. Для одномерной задачи сформулировать алгоритм сборки глобальной матрицы системы из локальных матриц жесткости и векторов нагрузки элементов. Рассмотреть случай линейных элементов. Как нужно учитывать граничные условия?
7. Сформулировать обобщенную по Галеркину постановку краевой задачи для одномерного уравнения Пуассона с граничным условием первого рода на левом конце и условием третьего рода на правом конце.
8. Дать определение квадратичного одномерного конечного элемента.
9. Для квадратичного одномерного конечного элемента дать определение вектора нагрузки и матрицы жесткости. Выписать для них формулы в случае равномерной сетки.
10. Для одномерной задачи сформулировать алгоритм сборки глобальной матрицы системы из локальных матриц жесткости и векторов нагрузки элементов. Рассмотреть случай квадратичных элементов. Как учесть граничные условия? Отдельно рассмотреть случай граничных условий третьего рода на правом конце.
11. Рассмотреть первую краевую задачу для двумерного уравнения Пуассона в единичном квадрате. Сформулировать обобщенную постановку задачи в форме Галеркина.
12. Описать триангуляцию единичного квадрата с помощью прямоугольных равнобедренных треугольников. В случае линейных элементов дать определение матрицы узлов, матрицы индексов, локальных координат и барицентрических координат. Дать определение функций формы линейного элемента и определение самого линейного элемента.
13. Рассмотреть конечно-элементную аппроксимацию первой краевой задачи для двумерного уравнения Пуассона в единичном квадрате. В случае линейных конечных элементов выписать формулы для матрицы жесткости и вектора нагрузки отдельного элемента. Сформулировать алгоритм сборки глобальной матрицы системы и учета граничных условий.
14. Описать триангуляцию единичного квадрата с помощью прямоугольных равнобедренных треугольников. В случае квадратичных элементов дать определение матрицы узлов, матрицы индексов, локальных координат и барицентрических координат. Дать определение функций формы квадратичного элемента и определение самого квадратичного элемента.
15. Рассмотреть конечно-элементную аппроксимацию первой краевой задачи для двумерного уравнения Пуассона в единичном квадрате. В случае квадратичных конечных элементов выписать формулы для матрицы жесткости и вектора нагрузки отдельного элемента. Сформулировать алгоритм сборки глобальной матрицы системы и учета граничных условий.
16. Рассмотреть начально-краевую задачу для уравнения теплопроводности на отрезке с граничными условиями первого рода. Сформулировать обобщенную постановку задачи в форме Канторовича-Галеркина. Рассмотреть аппроксимацию функции 
по пространственной переменной с помощью разложения по базисным функциям – «крышкам». Получить систему обыкновенных дифференциальных уравнений (ОДУ) для функций 
.
17. Рассмотреть начально-краевую задачу для уравнения теплопроводности на отрезке с граничными условиями первого рода. Выписать в явном виде систему обыкновенных дифференциальных уравнений для функций , полученную решением задачи в форме Канторовича-Галеркина с помощью разложения по базисным функциям – «крышкам». Данный алгоритм иначе называют полудискретным методом конечных элементов (МКЭ). Сравнить систему полудискретного МКЭ с системой ОДУ в методе прямых (МП), когда пространственная производная аппроксимируется методом конечных разностей, а время остается непрерывным.
18. Рассмотреть начально-краевую задачу для уравнения теплопроводности. С помощью спектрального метода фон-Неймана провести сравнительный анализ устойчивости явной схемы Эйлера для полудискретного МКЭ и для метода прямых (МП). То же самое проделать для схемы Кранка-Николсона.
19. Рассмотреть начально-краевую задачу для уравнения теплопроводности на отрезке с нулевыми граничными условиями и с нулевой правой частью. Согласно методу прямых (МП)произвести дискретизацию по пространственной переменной и получить точное решение системы ОДУ с помощью разложения в конечный ряд Фурье по синусам.
20. Рассмотреть начально-краевую задачу для уравнения теплопроводности на отрезке с нулевыми граничными условиями и с нулевой правой частью. Вывести алгоритм спектрального метода решения задачи. Чем отличается спектральный метод от метода прямых? Каков порядок сходимости спектрального метода в случае, когда решение является бесконечно-дифференцируемой функцией?
21. Рассмотреть начально-краевую задачу для уравнения теплопроводности на отрезке с нулевыми граничными условиями и с ненулевой правой частью (с наличием источника тепла). Произвести пространственную аппроксимацию с помощью разложения в конечный ряд Фурье по синусам. Выписать систему ОДУ для Фурье-гармоник для случая спектрального метода(СМ) и для случая метода прямых(МП). Для явной схемы Эйлера и для схемы Кранка-Николсона сформулировать необходимые условия устойчивости для СМ и МП.
22. Рассмотреть начально-краевую задачу для уравнения Шредингера на отрезке с нулевыми граничными условиями и с нулевой потенциальной функцией. Применить к этой задаче разложение в конечный ряд Фурье по синусам. Для СМ и МП провести методом фон-Неймана анализ устойчивости явной схемы Эйлера и схемы Кранка-Николсона.
23. Быстрый алгоритм конечного синус-преобразования Фурье на основе комплексного БПФ.
24. Стандартная форма дискретного преобразования Фурье (ДПФ). Доказать свойство обратимости: при последовательном применении к произвольному вектору прямого и обратного ДПФ должен в точности восстановиться исходный вектор.
25. БПФ: алгоритм Кули-Тьюки для длины вектора 
.
26. Представить функцию с периодом 
в виде ряда Фурье в комплексной форме и написать дискретную аппроксимацию (конечный ряд Фурье). Представить непериодическую функцию в виде интеграла Фурье в комплексной форме и также написать дискретную аппроксимацию. Показать, что в дискретном анализе различие между рядом Фурье и интегралом Фурье практически исчезает.
27. Представить дискретные аналоги ряда Фурье и интеграла Фурье в стандартном виде, пригодном к применению БПФ.
28. Рассмотреть одномерное уравнение Шредингера для квантовой частицы в потенциале. Применить спектральную аппроксимацию второй пространственной производной. Доказать, что симметричная схема расщепления имеет третий порядок аппроксимации.
29. Сформулировать численный алгоритм для одномерного уравнения Шредингера для квантовой частицы в вакууме. Применить спектральную аппроксимацию второй пространственной производной и алгоритм БПФ.
30. Вывести вещественную форму конечного ряда Фурье исходя из комплексной формы. Для нечетной функции вывести формулы конечного синус-преобразования Фурье, а для четной функции – формулы конечного косинус-преобразования Фурье. Являются ли обратимыми конечные синус- и косинус-преобразования Фурье? (Свойство обратимости означает, что при последовательном применении к произвольному вектору прямого и обратного преобразования должен в точности восстановиться исходный вектор).
31. Рассмотреть краевую задачу для уравнения теплопроводности в прямоугольнике, заполненном слоистой средой, однородной в боковом направлении (вдоль оси 
) и неоднородной вдоль оси 
. В случае теплоизолированных боковых стенок применить разложение в конечный ряд Фурье по косинусам и метод прогонки для коэффициентов Фурье, зависящих от .
32. Выписать разложение в интеграл Фурье вещественного сигнала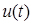 
. Применить комплексную и вещественную форму интеграла Фурье. Для вещественной формы рассмотреть частные случаи четной и нечетной функций 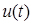.Для гармонического сигнала 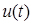определить сопряженный сигнал 
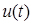. Выразить амплитуду и фазу гармонического сигнала через функци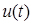и и .
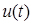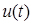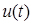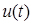33. Для вещественного сигнала определить сопряженный по Гильберту сигнал с помощью разложений в интеграл Фурье. Дать определение аналитического сигнала. Выразить амплитуду и фазу сигнала через функции и .Доказать свойство гармонического соответствия: в случае гармонического сигнала амплитуда и фаза, выраженные через функции и , совпадают с истинными амплитудой и фазой.
34. Установить связь спектров основного сигнала и сопряженного по Гильберту сигнала. Сформулировать алгоритм вычисления преобразования Гильберта с помощью БПФ.
35. Дать определение преобразования Гильберта через интеграл в смысле главного значения по Коши. Доказать, что это определение эквивалентно определению сопряженного по Гильберту сигнала с помощью разложений в интеграл Фурье
36. Выписать систему уравнений Максвелла для линейной среды. Показать, что в 2-мерном случае 
система из 6 уравнений распадается на 2 независимые подсистемы из трех уравнений. Выписать подсистемы для 1-мерного случая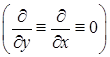 
. Показать, что одномерная система уравнений Максвелла эквивалентна одномерному волновому уравнению и системе уравнений одномерной акустики
37. Сформулировать постановку пространственно-одномерных начально-краевых задач для волнового уравнения и для системы уравнений Максвелла. Установить связь между начальными условиями (при 
), при которой обе постановки задач эквивалентны.
Точное решение задачи Коши на бесконечной прямой, выраженное через римановы инварианты.
38. Вывод неотражающих граничных условий типа PML на примере одномерной системы уравнений Максвелла. Сформулировать начально-краевую задачу для системы уравнений Максвелла в вакууме с неотражающими условиями типа PML.
39. Вывод неотражающих PML-слоев в случае гармонической временной зависимости. Интерпретация PML-слоя как формально однородной среды, но с пространственной координатой, смещенной в комплексную плоскость.
40. Уравнение Гельмгольца в двумерном волноводе, направленном по оси 
, c 
.
Задача нахождения нормальных волноводных мод. Применение неотражающих граничных условий типа PML для волноводов, аналогичных потенциальным барьерам в квантовой механике.
41. Задача о распространении волны в двумерном волноводе. Малоугловое (параболическое) приближение М.А. Леонтовича. Постановка начально-краевой задачи для уравнения типа Шредингера с PML-условиями на боковых границах.
42. Для одномерной системы уравнений Максвелла написать разностную схему на шахматной сетке. Как аппроксимировать начальные условия для магнитного поля со вторым порядком по времени? Доказать, что вне PML-слоев данная схема имеет второй порядок аппроксимации по времени и пространству.
43. Вывести необходимое условие устойчивости разностной схемы на шахматной сетке для одномерной системы уравнений Максвелла.
44. Рассмотреть систему уравнений Максвелла в вакууме с двумя пространственными переменными. Написать разностную схему на шахматной сетке. Доказать, что схема имеет второй порядок аппроксимации по времени и пространству. Вывести необходимое условие устойчивости разностной схемы.
45. Написать разностную схему Йи (Yee) для полноразмерной системы уравнений Максвелла в вакууме. Дать геометрическую интерпретацию. Объяснить порядок вычислений по разностной схеме. Ответить на вопрос о порядке аппроксимации и необходимом условии устойчивости (без доказательства).
Дополнительная литература
В.Б. Андреев. Лекции по методу конечных элементов: Учебное пособие. - М.: Издательский отдел факультета ВМиК МГУ им. М.В. Ломоносова (лицензия ИД N 05899 от 24.09.2001 г.); МАКС Пресс, 2010. - 2-е изд., испр. и доп. -- 264 с.
Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. Численные методы — 6-е изд. — М.: БИНОМ. Лаборатория знаний, 2008. — 636 с.: ил.
L.N. Trefethen. Finite difference and spectral methods for ordinary and partial dufferential equations. Cornell University, USA, 1996.
Вайнштейн Л.А., Вакман Д.Е. Разделение частот в теории колебаний и волн. – М.: Наука. Главная редакция физико-математической литературы, 1983. – 288 с.
A. Taflove, S.C.Hagness. Computational Electrodynamics: The Finite-Difference Time-Domain Method. ARTECH HOUSE, INC, 2005
A. Bondeson, T. Rylander, and P. Ingelstreom. Computational Electromagnetics. 2005 Springer Science+Business Media, Inc.