Методы:
- Метод пристального взгляда
Этот метод основан на следующем теоретическом положении: «Если функция возрастает в области определения и число входит в множество значений, то уравнение имеет единственное решение».
Для реализации метода, основанного на данном утверждении, требуется:
a) Выделить функцию, которая фигурирует в уравнении.
b) Записать область определения данной функции.
c) Доказать ее монотонность в области определения.
d) Угадать корень уравнения.
e) Обосновать, что других корней нет.
f) Записать ответ.
Пример:.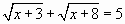 
Рассмотрим функцию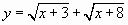 
.
Найдем область определения данной функции:
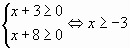
Данная функция является монотонно возрастающей.
Для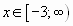 
,эта функция будет принимать наименьшее значение при 
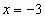, а далее только возрастать. 
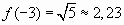. Число 5 принадлежит области значения, следовательно, согласно утверждению 
.
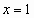Проверкой убеждаемся, что это действительный корень уравнения.
- Метод возведения обеих частей уравнений в одну и ту же степень.
Теорема.
Если возвести обе части уравнения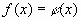 
(1) в натуральную степень 
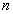, то уравнение 
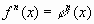(2) является следствием уравнения (1).
,
,
.
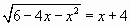
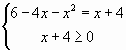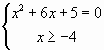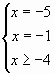Ответ: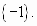 
- Решение уравнений с использованием замены переменной.
Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.
Пример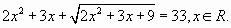 
Пусть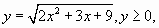 
тогда исходное уравнение примет вид:
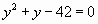, корни которого 
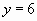и 
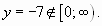
Решая уравнение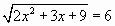 
, получаем 
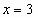и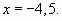 
Ответ: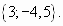 
- Метод выделения полных квадратов при решении иррациональных уравнений.
При решении некоторых иррациональных уравнений полезна формула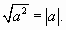 
Пример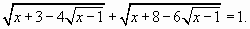 
Преобразуем уравнение следующим образом:
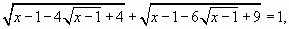
или
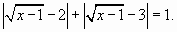
Обозначим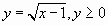 
и решим полученное уравнение методом интервалов.
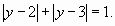
Разбирая отдельнослучаи 
, находим, что решениями последнего уравнения являются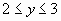 
.
Возвращаясь к переменной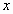 
, получаем неравенства
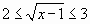
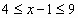
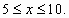
Ответ: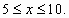
- Иррациональные уравнения, содержащие степени выше второй.
Если уравнение имеет вид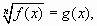 
то его можно решить, возводя обе части этого уравнения в степень 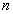. Полученное уравнение 
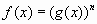при нечетном 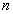равносильно данному уравнению, а при четном 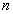является его следствием, аналогично рассмотренному выше случаю при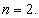 
Пример 1.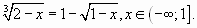 
Возведем обе части уравнения в куб:
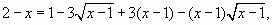или
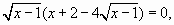которое равносильно совокупности двух уравнений:
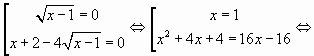
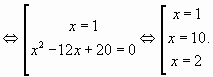
Ответ: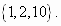 
Пример 2.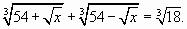 
Здесь, очевидно,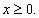 
Возведем в куб обе части уравнения, получим:
,
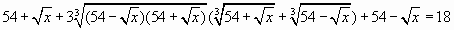или
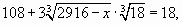
или
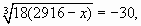
или
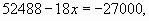
или
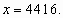
Проверка подтверждает, что это корень уравнения.
Ответ: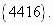 
Пример 1
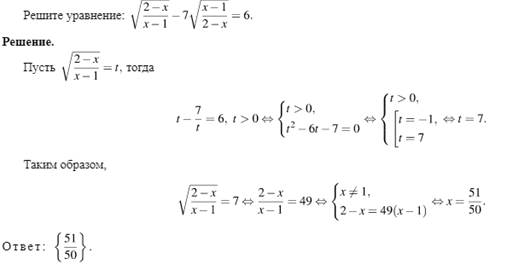
Рациональные уравнения
Алгоритм:
1. Перенести все слагаемые в левую часть, чтобы в правой части получился 0.
2. Преобразовать и упростить левую часть, привести все дроби к общему знаменателю.
3. Полученную дробь приравнять к 0, по следующему алгоритму: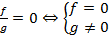 
.
4. Записать те корни, которые получились в первом уравнении и удовлетворяют второму неравенству, в ответ.
Пример 1.
Пример 2.
