Пример 1
Решите уравнение 15^cosx=3^cosx⋅5^sinx
Это показательно-тригонометрическое уравнение.
15^cosx=3^cosx⋅5^sinx
Обратим внимание, что 15 можно представить, как 3⋅5. Вряд ли это простое совпадение. Используя свойства степеней разложим 15 на множители.
3^cosx⋅5^cosx=3^cosx⋅5^sinx
Перенесем выражение из правой части в левую.
3^cosx⋅5^cosx−3^cosx⋅5^sinx=0
Вынесем за скобки 3^cosx.
3^cosx(5^cosx−5^sinx)=0
Решаем методом расщепления.
3^cosx=0 или 5^cosx−5^sinx=0
нет корней 5^cosx=5^sinx
cosx=sinx
сtgx=1
x=π/4+πk, k∈Z
В какую степень надо возвести тройку, чтоб она стала нулем? Ни в какую, положительное число в любой степени останется положительным числом. Поэтому у первого уравнения нет решения.
Во втором уравнении перенесем 5^sinx вправо.
Имеем показательное уравнение. Решаем его как обычно - «убираем» основания степеней.
Делим уравнение на sinx. Это можно сделать т.к. sinx=0 не будет решением уравнения. Значит синус икс – не ноль, и поэтому на него можно делить.
Решаем базовое тригонометрическое уравнение.
Ответ: x=π/4+πk, k∈Z.
Пример 2
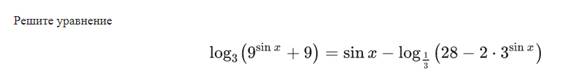

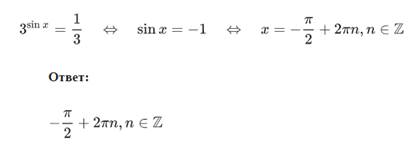
Пример 3

Логарифмические уравнения
Основные методы решения логарифмических уравнений:
1 метод. Использование определения логарифма: loga f(x)=b ⇔ f(x)=ab, a>0, a≠1.
2 метод. Использование свойств логарифма:
logacb=1clogab
c⋅logab=logabc
logab+logac=loga(bc)
logab−logac=loga(bc)
loganb=1n⋅logab
loganbm=mn⋅logab
loga1=0, a>0,a≠1
logaa=1 (a>0,a≠1)
3 метод. Введение новой переменной (замена):
Замена logax = t позволяет свести логарифмическое уравнение к более простому алгебраическому уравнению относительно t.
4 метод. Переход к новому основанию:
logab=logcblogca (c>0; ≠1).
logab=1logba, (b≠1).
5 метод. Логарифмирование:
Берется логарифм от правой и левой частей уравнения.
6 метод. Минимальный-максимальный:
Теорема: Если a>1, то функция f(x)=logax является монотонно возрастающей, если 0<a<1, то функция f(x)=logax является монотонно убывающей.
Пример 1

Пример 2
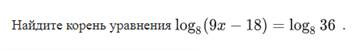

Пример 3
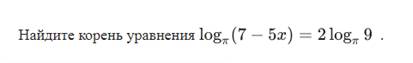
Показательные уравнения
Основные свойства степеней, при помощи которых преобразуются показательные уравнения:
а>0, b>0.
а^0 = 1, а^1= а.
а^m/n=, где m и n– натуральные числа.
a^-n = 1/ а^n
a^n × a^m = a^n+m
a^n/a^m = a^n-m
(a^n)m = a^n-m
(ab)^n = a^n×b^n
(a/b)^n = a^n/b^n.
При решении показательных уравнений пользуются также следующими свойствами показательной функции: y = a^x, a > 0, a не равно 1:
1. a^x>0, при всех a>0 и x принадлежит R.
2. a^x1 =a^x2, следовательно х1=х2.
Методы решения уравнений:
- Одним из методов решения показательных уравнений является метод логарифмирования.
- Следующим методом решения показательного уравнения является введение новой переменной:
Например, чтобы решить уравнение 9^{3x+3}+3^{2x+9}=739 можно воспользоваться подстановкой y=3^{x} приведение показательного уравнения к квадратному.
- Метод вынесения общего множителя за скобки.
- Метод использования монотонности показательной функции.
Пример 1

Пример 2


Пример 3
