К традиционным плитным материалам на основе древесины относятся:
а) древесно-волокнистые плиты сухого способа производства (ДВПс) на фенольных связующих;
б) древесно-стружечные плиты на карбамидных (ДСПк) и на фенольных связующих (ДСПф);
в) древесно-стружечные плиты на каустическом магнезите МДП;
г) цементно-стружечные плиты на портландцементе ЦСП;
д) березовая (ФСФ, ФК) и бакелизированная (ФБС) фанера.
Их расчетные характеристики были подробно изучены не позднее конца 70-х лет прошлого века и содержатся в СНиП II-25-80 (или в Пособии к нему) и в двух последующих поколениях нормативных документов – Сводов правил.
Из относительно новых плитных материалов хорошо изучен т.н. брус многослойный клееный из однонаправленного шпона (LVL, ультралам), характеристики которого впервые появились в СП 64.13330.2011.
Другой распространенный листовой материал ориентированные стружечные плиты ОСП (англ. OSB), выпускаемый большим числом производителей в разных странах, отличается нестабильным качеством и изучен недостаточно. В отечественные нормы проектирования он пока не включен.
Прочностные и упругие характеристики древесных плитных материалов определяются по действующим стандартам на методы их испытаний. Важнейшая особенность нормирования характеристик плитных материалов заключается в учете масштабного фактора – пониженной прочности крупноразмерных плит по сравнению с пределом прочности испытываемых мелкоразмерных полосок, выпиливаемых из плит.
Нормативные сопротивления древесных плит вычисляются с обеспеченностью 0,95 по формуле
R н = 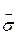 (1 ‑ 1,65 v),
(1 ‑ 1,65 v),
а расчетные сопротивления с обеспеченностью 0,99 по формуле
RА = R н K р / γ m,
где γ m = (1 ‑ ηн v)/(1 ‑ η v) = (1 ‑ 1,65 v)/(1 ‑ 2,33 v) – коэффициент надежности по материалу,
K р = 0,8 – масштабный коэффициент, учитывающий относительное увеличение прочности мелких опытных образцов по сравнению со средней прочностью всей плиты, имеющей размеры на 1-2 порядка большие, чем ширина образца.
ηн и η – квантили нормативного и расчетного сопротивлений для нормального закона распределения предела прочности.
Когда мы говорим о приведенных в нормах характеристиках прочности материалов, мы понимаем, что для их получения были обработаны результаты обширных многолетних исследований, включающие испытаний сотен и тысяч образцов. Поэтому здесь мы уходим от распределения Стьюдента и оперируем квантилями нормального закона распределения
Рассмотрим для примера прочностные характеристики древесно-волокнистой плиты сухого способа производства из табл. 12 «Пособия по проектированию деревянных конструкций» (к СНиП II-25-80) при работе ее на растяжение. Базовое расчетное сопротивление R р было установлено в СНиП II-25-80 с учетом коэффициента длительного сопротивления m дл = 0,54.
| Материал | Временное сопротивление R вр, МПа | v | m дл | γ m | Нормативное сопротивление, R н, МПа | Расчетное сопротивление по СНиП II-25-80 R р, МПа |
| Растяжение | ||||||
| ДВПс | 23,6 | 0,171 | 0,54 | 1,19 | 6,15 |
Расчетное сопротивление R р = 6,15 МПа в этой таблице было вычислено по формуле
R р = R н m дл / γ m.
По современной методике нормирования ГОСТ 27751-2014 и СП 64.13330.2017 коэффициент длительного сопротивления m дл = 0,54 из базового расчетного значения следует исключить. Тогда базовое расчетное сопротивление для современных норм СП 20.13330.2017 оказывается равным
R рА = R р/ m дл = 6,15 / 0,54 = 11,4 МПа.
Определим его обеспеченность, зная численные значения коэффициента вариации предела прочности плиты v = 0,171 и коэффициента надежности ее по материалу γ m = 1,19.
Вычислим принятое в нормах значение квантиля расчетного сопротивления η. Зная, что значение квантиля нормативного сопротивления для любых материалов ηн равно 1,65, получаем простейшее уравнение
γ m = (1 ‑ ηн v)/(1 ‑ η v) = (1 – 1,65×0,171)/(1 ‑ η×0,171) = 1,19.
Из него получаем значение η = [(1 – 1,65×0,171)/1,19 ‑ 1]/0,171 = 2,320 ≈ 2,326 для нормального закона при односторонней вероятности 0,99.
Таким образом, мы убедились, что расчетное сопротивление растяжению R рА древесно-волокнистой плиты установлено в нормах действительно с обеспеченностью по минимуму 0,99.
Применим эту же процедуру для оценки обеспеченности нормативного сопротивления:
R нр = Rр вр(1 ‑ ηн v) = 23,6(1 ‑ ηн 0,171) = 17 МПа.
Отсюда ηн = (1 ‑ 17 / 23,6) / 0,171 = 1,635 ≈ 1,645 для обеспеченности 0,95.
Небольшая разница получилась в обоих случаях, как для расчетного, так и для нормативного сопротивлений, из-за округления численных значений прочностных характеристик древесно-волокнистой плиты. При этом очевидно, что нормативное сопротивление R н = 17 МПа имеет обеспечен-ность, близкую к предписанной ГОСТом и равную 0,95.