Работа и мощность тока. КПД источника тока
При прохождении электрического заряда q по любому участку цепи, на концах которого приложено напряжение U, электрическое поле за время t совершает над зарядами работу:
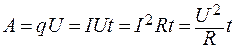 . (2.1)
. (2.1)
Разделив работу А на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке цепи:
 . (2.2)
. (2.2)
Полная мощность, развиваемая источником тока с ЭДС ε и внутренним сопротивлением r, замкнутым на сопротивление R, равна работе, совершаемой сторонними силами за единицу времени:
 . (2.3)
. (2.3)
Во внешней цепи выделяется мощность (полезная мощность)
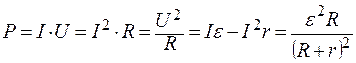 . (2.4)
. (2.4)
Максимальная полезная мощность
 (2.5)
(2.5)
достигается при R = r.
Отношение η=P/P0, равное
 , (2.6)
, (2.6)
называется коэффициентом полезного действия источника тока.
При R = r КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т. е. при R → ∞. В случае короткого замыкания (R =0) полезная мощность P = 0, и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
Закон Джоуля-Ленца
В случае, когда проводник неподвижен и химических превращений в нем не происходит, то работа тока целиком расходуется на нагревание проводника. Количество теплоты, выделяющееся в проводнике за конечный промежуток времени при прохождении постоянного тока I, рассчитывается по формуле
 . (2.7)
. (2.7)
Формула (2.7) выражает закон Джоуля-Ленца для участка цепи постоянного тока: количество теплоты, выделяемое постоянным электрическим током на участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.
Так как IR = U, то формулу (2.7) можно переписать в виде
 . (2.8)
. (2.8)
Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t, вычисляется по формуле
 . (2.9)
. (2.9)
Закон Джоуля-Ленца в дифференциальной форме (для данной точки проводника с током) имеет вид
 , (2.10)
, (2.10)
где ω − плотность тепловой мощности; σ − удельная электропроводность; Е − напряженность электрического поля в данной точке проводника; Е * − напряженность поля сторонних сил.
Примеры решения задач
Задача 1. За время τ = 20 с при равномерно возраставшей силе тока от нуля до Io в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Найти Io.
| Io –? | Решение:
Так как ток равномерно возрастает, то зависимость силы тока от времени имеет вид
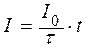 . (1) . (1)
|
| τ = 20 с R = 5 Ом Q = 4 кДж |
По закону Джоуля-Ленца за время dt в проводнике выделится количество тепла
 .
.
Полное количество тепла за время от 0 до τ
 .
.
Отсюда находим
 ;
;  .
.
Ответ: I0 = 11 А.
Задача 2. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление обмотки мотора R = 6 Ом.
| Pп –? η –? | Решение:
Полная мощность, потребляемая мотором:
 ,
Р0 = 1100 Вт. ,
Р0 = 1100 Вт.
|
| U = 220 В I = 5 А R = 6 Ом |
Мощность, выделяющаяся в виде тепла:
 .
.
Полезная мощность (механическая)
 .
.
КПД мотора
 ;
;
 .
.
Ответ: η = 86,4%.
Задача 3. Источник тока с ЭДС замкнут на реостат. При силе тока I1 = 0,2 А и I2 = 2,4 А на реостате выделяется одинаковая мощность. Найти:
1) при какой силе тока на реостате выделяется максимальная мощность?
2) чему равна сила тока короткого замыкания?
| I –? Iкз –? | Решение:
При силе тока I1 на реостате выделяется мощность
 ,
при силе тока I2 ,
при силе тока I2
 , ,
|
| I1 = 0,2 А | |
| I2 = 2,4 А P1 = P2 |
где R1 и R2 – сопротивления реостата в каждом случае. По условию P1 = P2, поэтому
 . (1)
. (1)
По закону Ома для полной цепи
 , (2)
, (2)
 . (3)
. (3)
Из (2) и (3) выражаем R1 и R2:
 ;
;  ,
,
подставив их в (1), получаем:
 .
.
Отсюда находим отношение  :
:
 ;
;
 .
.
Максимальная мощность выделяется при условии R = r, при этом ток
 . (4)
. (4)
Ток короткого замыкания
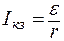 . (5)
. (5)
Произведем вычисления:
 ;
;  .
.
Ответ: I = 1,3 А; Iкз = 2,6 А.
Задача 4. При изменении внешнего сопротивления с R1 = 6 Ом до R2 = 21 Ом. КПД схемы увеличился вдвое. Чему равно внутреннее сопротивление источника тока r?
| r −? | Решение:
При сопротивлении R1 КПД источника тока
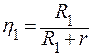 ,
а при сопротивлении R2 ,
а при сопротивлении R2
|
| R1 = 6 Ом R2 = 21 Ом η2 = 2η1 |
 .
.
Так как по условию задачи η2=2η1, то
 .
.
Отсюда выражаем r:
 ;
;
 .
.
Ответ: r = 14 Ом.
Задача 5. Две батареи с ЭДС ε1 = 20 В и ε2 = 30 В и внутренними сопротивлениями r1 = 4 Ом и r2 = 60 Ом соединены параллельно и подключены к нагрузке R = 100 Ом. Найти: 1) мощность, которая выделяется в нагрузке; 2) параметры ε и r генератора, которым можно заменить батареи без изменения тока в нагрузке; 3) КПД этого генератора.
| P –? ε, r –? η –? | Решение:
 Рис. 52
Рис. 52
|
| ε1 = 20 В ε2 = 30 В r1 = 4 Ом r2 = 60 Ом R = 100 Ом |
Используя правила Кирхгофа, найдем токи I1, I2, I в узле A:
 . (1)
. (1)
Для контура a с обходом против часовой стрелки
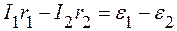 . (2)
. (2)
Для контура b с обходом против часовой стрелки
 . (3)
. (3)
Решим систему линейных уравнений (1) – (3) относительно I1, I2, I.
Из (1) выразим I
 . (4)
. (4)
Подставим в (3)

или
 . (5)
. (5)
Умножая уравнение (2) на R, а уравнение (5) – на r1, и складывая их, получаем:

 . (6)
. (6)
Подставляя (6) в выражение (2), находим I1:
 .
.
Отсюда
 . (7)
. (7)
Подставляя выражения (6) и (7) в (4), находим I:
 . (8)
. (8)
В нагрузке выделяется мощность:
 ;
;
 .
.
Находим параметры генератора. Если данные в задаче батареи заменить на одну с ЭДС ε и внутренним сопротивлением r, то через сопротивление R потек бы ток
 . (9)
. (9)
Преобразуем выражение (8), поделив числитель и знаменатель дроби на (r1+r2), получим
 . (10)
. (10)
Для того чтобы эти выражения были одинаковыми, необходимо выполнение условий:
 ;
;
 ;
;

 .
.
КПД этого генератора в данной схеме
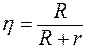 ;
;

Ответ: η = 96,4 %.