ТЕМА 2. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЯ. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Выборочное среднее. Выборочная дисперсия.
Выборочное среднее квадратическое отклонение
В теории вероятностей определили числовые характеристики для случайных величин, с помощью которых можно сравнивать однотипные случайные величины. Аналогично можно определить ряд числовых характеристик и для выборки. Поскольку эти характеристики вычисляются по статистическим данным (по данным, полученным в результате наблюдений), их называют статистическими характеристиками.
Пусть дано статистическое распределение выборки объема  :
:

| 
| 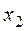
| 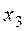
| 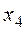
| 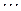
| 
|
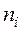
| 
| 
| 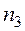
| 
| 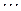
| 
|
где 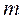 - число вариантов.
- число вариантов.
Определение. Выборочным средним  называется среднее арифметическое всех значений выборки:
называется среднее арифметическое всех значений выборки:
 .
.
Выборочное среднее можно записать и так: 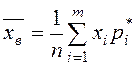 ,
,
где  - частость.
- частость.
В случае интервального статистического ряда в качестве  берут середины интервалов, а
берут середины интервалов, а 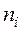 - соответствующие им частоты.
- соответствующие им частоты.
Определение. Выборочной дисперсией  называется среднее арифметическое квадратов отклонений значений выборки от выборочного среднего
называется среднее арифметическое квадратов отклонений значений выборки от выборочного среднего  :
:
 или
или 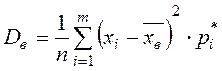 .
.
Выборочное среднее квадратическое выборки определяется формулой:
 .
.
Особенность  состоит в том, что оно измеряется в тех же единицах, что и данные выборки.
состоит в том, что оно измеряется в тех же единицах, что и данные выборки.
Если объем выборки мал ( ), то пользуются исправленной выборочной дисперсией:
), то пользуются исправленной выборочной дисперсией:
 .
.
Величина 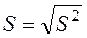 называется исправленным средним квадратическим отклонением.
называется исправленным средним квадратическим отклонением.
Выборочные начальные и центральные моменты.
Асимметрия. Эксцесс.
Приведем краткий обзор характеристик, которые наряду с уже рассмотренными применяются для анализа статистических рядов и являются аналогами соответствующих числовых характеристик случайной величины.
Среднее выборочное и выборочная дисперсия являются частным случаем более общего понятия – момента статистического ряда.
Определение. Начальным выборочным моментом порядка  называется среднее арифметическое
называется среднее арифметическое  - х степеней всех значений выборки:
- х степеней всех значений выборки:
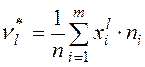 или
или 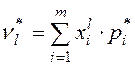 .
.
Из определения следует, что начальный выборочный момент первого порядка: 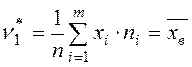 .
.
Определение. Центральным выборочным моментом порядка  называется среднее арифметическое
называется среднее арифметическое  - хстепеней отклонений наблюдаемых значений выборки от выборочного среднего
- хстепеней отклонений наблюдаемых значений выборки от выборочного среднего  :
:
 или
или 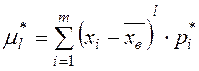 .
.
Из определения следует, что центральный выборочный момент второго порядка:
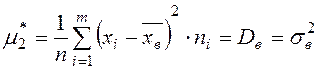 .
.
Определение. Выборочным коэффициентом асимметрии называется число  , определяемое формулой:
, определяемое формулой: 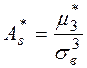 .
.
Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.
Если  , то более пологий «спуск» полигона наблюдается слева; если
, то более пологий «спуск» полигона наблюдается слева; если 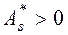 - справа. В первом случае асимметрию называют левосторонней, а во втором - правосторонней.
- справа. В первом случае асимметрию называют левосторонней, а во втором - правосторонней.
Определение. Выборочным коэффициентом эксцесса или коэффициентом крутости называется число 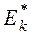 , определяемое формулой:
, определяемое формулой:
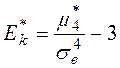 .
.
Выборочный коэффициент эксцесса служит для сравнения на «крутость» выборочного распределения с нормальным распределением.
Коэффициент эксцесса для случайной величины, распределенной по нормальному закону, равен нулю.
Поэтому за стандартное значение выборочного коэффициента эксцесса принимают 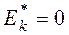 .
.
Если  , то полигон имеет более пологую вершину по сравнению с нормальной кривой; если
, то полигон имеет более пологую вершину по сравнению с нормальной кривой; если  , то полигон более крутой по сравнению с нормальной кривой.
, то полигон более крутой по сравнению с нормальной кривой.
Вычисление числовых характеристик выборки
Таблица 6

| 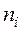
| 
| 
| 
| 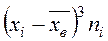
| 
|

| 
| |||||

| 
| |||||

| 
| |||||
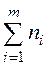
| 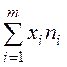
| 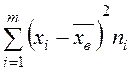
| 
| 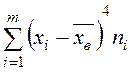
|
 - середины интервалов;
- середины интервалов; 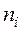 - частоты;
- частоты;  - объем выборки;
- объем выборки;
с помощью суммы 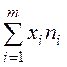 находим
находим  ;
;
с помощью суммы 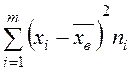 находим
находим  и
и  ;
;
с помощью суммы  находим
находим  ;
;
с помощью суммы 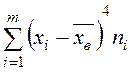 находим
находим 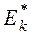 .
.