Общая схема принятия решения

Курсовая работа

На тему: «Математические модели поведения производителей»

Выполнила: студентка II курса группа А

Полева Е. Л.

Проверила: Жилина Л. С.

Донецк-2008

Содержание

Определение математической модели

Общая схема принятия решений

Типы задач на оптимизацию

Модель фирмы

Задачи

Список литературы

Определение математической модели

Важным фактором, определяющим роль математики в различных приложениях, является возможность описания наиболее существенных черт и свойств изучаемого объекта на языке математических символов и соотношений. Такое описание принято называть математическим моделированием или формализацией.

Определение 1. Математической моделью реального объекта (явления) называется ее упрощенная, идеализированная схема, составленная с помощью математических символов и операций (соотношений).

Для построения математической модели конкретной экономической задачи (проблемы) рекомендуется выполнение следующей последовательности работ:

1. Определение известных и неизвестных величин, а также существующих условий и предпосылок (что дано и что требуется найти?);

2. Выявление важнейших факторов проблемы;

3. Выявление управляемых и неуправляемых параметров;

4. Математическое описание посредством уравнений, неравенств, функций и иных отношений взаимосвязей между элементами модели (параметрами, переменными), исходя из содержания рассматриваемой задачи.

Известные параметры задачи относительно ее математической модели считаются внешними (заданными априори, т. е. до построения модели). В экономической литературе их называют экзогенными переменными. Значение же изначально неизвестных переменных вычисляются в результате исследования модели, поэтому по отношению к модели они считаются внутренними. В экономической литературе их называют эндогенными переменными.

С точки зрения назначения, можно выделить описательные модели и модели принятия решения. Описательные модели отражают содержание и основные свойства экономических объектов как таковых. С их помощью вычисляются числовые значения экономических факторов и показателей.

Модели принятия решения помогают найти наилучшие варианты плановых показателей или управленческих решений. Среди них наименее сложным являются оптимизационные модели, посредством которых описываются (моделируются) задачи типа планирования, а наиболее сложными —игровые модели, описывающие задачи конфликтного характера с учетом пересечения различных интересов. Эти модели отличаются от описательных тем, что в них имеется возможность выбора значений управляющих параметров (чего нет в описательных моделях).

Общая схема принятия решения

В математической экономике трудно переоценить роль моделей принятия решения. Наиболее частое применение находят те из них, которые сводят исходные задачи оптимального планирования производства, рационального распределения ограниченных ресурсов и эффективной деятельности экономических субъектов к экстремальным задачам, к задачам оптимального управления и к игровым задачам. Какова же общая структура таких моделей?

Любая задача принятия решения характеризуется наличием лица или лиц, преследующих определенные цели и имеющих для этого определенные возможности. Поэтому для выявления основных элементов модели принятия решения требуется ответить на следующие вопросы:

Ÿ кто принимает решение?

Ÿ каковы цели принятия решения?

Ÿ в чем состоит принятие решения?

Ÿ каково множество возможных вариантов достижения цели?

Ÿ при каких условиях происходит принятие решения?

Итак перед нами некая общая задача принятия решения. Для построения ее формальной схемы (модели) введем общие обозначения.

Буквой N обозначим множество всех, принимающих решение сторон. Пусть N={1,2,..., n}, т.е. имеется всего n участников идентифицируемых только номерами. Каждый элемент называется лицом, принимающим решение (ЛПР). (например, отдельная личность, фирма, плановый орган большого концерна, правительства и др.).

Предположим, что множество всех допустимых решений (альтернатив, стратегий) каждого ЛПР предварительно изучено и описано математически (например, в виде системы неравенств). Обозначим их через X₁, X₂,..., X_n. После этого процесс принятия решения всеми ЛПР сводится к следующему формальному акту: каждое ЛПР выбирает конкретный элемент из своего допустимого множества решений 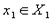, ,..., . В результате получается набор х =(х1,...,хn) выбранных решений, который мы называем ситуацией.

Для оценки ситуации х с точки зрения преследуемых целей ЛПР строятся функции f₁,..., f_n (называемыми целевыми функциями или критериями качества), ставящие в соответствие каждой ситуации х числовые оценки f₁(x),..., f_n(x) (например, доходы фирм в ситуации х, или их затраты и т. д.). Тогда цель i -го ЛПР формализуется следующим образом: выбрать такое свое решение , чтобы в ситуации х =(х₁,...,х_n) число f_i(х) было как можно большим (или меньшим). Однако достижение этой цели от него зависит частично в виду наличия других сторон, влияющих на общую ситуацию x с целью достижения своих собственных целей. Этот факт пересечения интересов (конфликтность) отражается в том, что функция f_i помимо x_i зависит и от остальных переменных x_j (j i). Поэтому в моделях принятия решения со многими участниками их цели причодится формализовать иначе, чем максимизация или минимизация значений функции f_i(х). Наконец, пусть нам удалось математически описать все те условия, при которых происходит принятие решения. (описание связей между управляемыми и неуправляемыми переменными, описание влияния случайных факторов, учет динамических характеристик и т. д.). Совокупность всех этих условий для простоты обозначим одним символом .

Таким образом, общая схема задачи принятия решения может выглядеть так:

(1)

Конкретизируя элементы модели (1.6.1.), уточняя их характеристики и свойства, можно получть тот или иной конкретный класс моделей принятия решения. Так если в (1.6.1.) N состоит только из одного элемента (n=1), а все условия и предпосылки исходной реальной задачи можно описать в виде множества допустимых решений этого единственного ЛПР, то из (1.6.1.) получаем структуру оптимизационной (экстремальной) задачи: < Х, f >. В этой схеме ЛПР может рассматриваться как планирующих орган. С помощью данной схемы можно написать экстремальные задачи двух видов:

(2)

Если в экстремальной задаче явно учитывается фактор времени, то она называется задачей оптимального управления. Если n 2, то (1.6.1.) является общей схемой задачи принятия решения в условиях конфликта, т. е. в тех ситуациях, когда имеет место пересечение интересов двух или более сторон.

Часто у ЛПР имеется не одна, а несколько целей. В этом случае из (1) получаем схему , где все функции f₁(x),..., f_n(x) определены на одном и том же множестве Х. Такие задачи называются задачами многокритериальной оптимизации.

Имеются классы задач принятия решения, получившие свои названия исходя из их назначения: системы массового обслуживания, задачи управления запасами, задачи сетевого и календарного планирования, теория надежности и др.

Если элементы модели (1) не зависят явно от времени, т. е. процесс принятия решения сводится к мгновенному акту выбора точки из заданного множества, то задача называется статической. В противном случае, т. е. когда принятие решения представляет собой многоэтапный дискретный или непрерывный во времени процесс, задача называется динамической. Если элементы модели (1) не содержат случайных величин и вероятностных явлений, то задача называется детерминированной, в противном случае — стохастической.