Типы задач на оптимизацию

Задача оптимального раскроя материала. Фирма изготавляет изделие состоящее из р деталей. Причем в одно изделие эти детали входят в количествах k₁,..., k_r. С этой целью производится раскрой m партий материала. В i-ой партии имеется b_i единиц материала. Каждую единицу материала можно раскроить на детали n способами. При раскрое единицы i -ой партии j -м способом получается а_ijr деталей r-го вида. Требуется составить такой план раскроя материала, чтобы из них получить максимальное число изделий.

Транспортная задача. Имеется n поставщиков и m потребителей одного и того же продукта. Известны выпуск продукции у каждого поставщика и потребности в ней каждого потребителя, затраты на перевозки продукции от поставщика к потребителю. Требуется построить план транспортных перевозок с минимальными транспортными расходами с учетом предложения поставщиков и спроса потребителей.

Задача о назначениях на работу. Имеется n работ и n исполнителей. Стоимость выполнения работы i исполнителем j равна c_ij. Нужно распределить исполнителей на работы так, чтобы минимизировать затраты на оплату труда.

3адача о смесях (о рационе). Из m видов исходных материалов каждый из которых состоит из n компонент, составить смесь, в которой содержание компонент должно быть не меньше b₁,...,b_n. Известны цены единиц материалов с₁,...,с_m и удельный вес j- го компонента в единице i-го материала. Требуется составить смесь, в которой затраты будут минимальными.

Задача о рюкзаке. Имеется n предметов. Вес предмета i равен р_i, ценность – сi (i=1,...,n). Требуется при заданной ценности груза выбрать совокупность предметов минимального веса.

Задача о коммивояжере. Имеется n городов и заданы расстояния c_ij между ними (j,i=1,...,n). Выезжая из одного (исходного) города, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в исходный город. Нужно определить в каком порядке следует обьезжать города, чтобы суммарное пройденное расстояние было наименьшим.

Задача о станках. На универсальном станке обрабатываются одинаковые партии из n деталей. Переход от обработки детали i к обработке детали j требует переналадки станка, которая занимает c_ij времени. Требуется определить последовательность обработки деталей, при которой общее время переналадок станка при обработку партии деталей минимально.

Задача о распределении капиталовложений. Имеется n проектов, причем для каждого проекта j известны ожидаемый эффект от его реализации и необходимая величина капиталовложений g_j. Общий объем капиталовложений не может превышать заданной величины b. Требуется определить, какие проекты необходимо реализовать, чтобы суммарный эффект был наибольшим.

Задача о размещении производства. Планируется выпуск m видов продукции, которые могли бы производиться на n предприятиях (n>m). Издержки производства и сбыта единицы продукции, плановый объем годового производства продукции и плановая стоимость единицы продукции каждого вида известны. Требуется из n предприятий выбрать такие m, каждое из которых будет производить один вид продукции.

Модель фирмы

 

Пусть производственная фирма выпускает один вид продукции или много видов, но в постоянной структуре. Тогда годовой выпуск фирмы в натурально-вещественной форме X - это число единиц продукции одного вида или число много номенклатурных агрегатов. Для производства продукции фирма использует настоящий труд L (среднее число занятых в год либо отработанные за год человеко-часы) прошлый труд в виде средств труда К (основные производственные фонды) и предметов труда М (затраченные за год топливо, энергия, сырьё, материалы, комплектующие и т.п.).

Каждый из этих трех агрегированных видов ресурсов (труд, фонды и материалы) имеет определенное число разновидностей (труд разной квалификации, оборудование различного вида и т.п.). Обозначим вектор-столбец возможных объемов затрат различных видов ресурсов через х=(х₁..., х_n)'. Тогда технология фирмы определяется ее производственной функцией, выражающей связь между затратами ресурсов и выпуском:

X=F(x). (3)

 

Предполагается, что F(x) является дважды непрерывно-дифференцируемой и неоклассической, кроме того, ее матрица вторых производных отрицательно определена.

Если цена единицы продукции равна р, а цена единицы ресурса j-го вида — wj,j= 1,..., n, то каждому вектору затрат х отвечает прибыль П(х) = pF(x)-wx, (4) где w= (w1, w2..., wn) — вектор-строка цен ресурсов. Цены ресурсов имеют естественный и понятный смысл: если хj — среднегодовое число занятых определенной профессии, то wj - годовая заработная плата одного работника данной профессии; если хj — по-купные материалы (топливо, энергия и т.п.), то wj — покупная цена единицы данного материала; если хj — производственные фонды определенного вида, то wj — годовая арендная плата за единицу фондов или стоимость поддержания единицы фондов в исправности, если фирма владеет этими средствами.

В (4) R = pX= pF(x) - стоимость годового выпуска фирмы или ее годовой доход, С = wx — издержки производства или стоимость затрат ресурсов за год.

Если нет других ограничений на размеры вовлекаемых в производ-ство ресурсов, кроме естественного требования их неотрицательности, то задача на максимум прибыли приобретает вид

max [pF(x)- wx] (5)

 

Это задача нелинейного программирования с п условиями неотрицательности х >0, необходимыми условиями ее решения являются условия Куна-Таккера (см. В. А. Колемаев «Математическая экономика», с.236, Приложение 4)

 

(6)

Если в оптимальном решении использованы все виды ресурсов, т.е. х* >0, то условия (6) принимают вид

 

 

или (7)

 

 

т.е. в оптимальной точке стоимость предельного продукта данного pесурса должна равняться его цене.

Точно такое же по форме решение имеет задача на максимум выпуска при заданном объеме издержек

max F(x), (8) wx 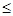С, х 0

 

Это задача нелинейного программирования с одним линейным ограничением и условием неотрицательности переменных. Согласно теории (см. Приложение 4) вначале строим функцию Лагранжа

L(x, ) = F(x) + (C-wx),

 

затем максимизируем ее при условии неотрицательности переменных. Для этого необходимо выполнение условий Куна—Таккера

 

(9)

 

Как видим, условия (9) полностью совпадают с (6), если

Пример. Выпуск однопродуктовой фирмы задается следующей проиводственной функцией Кобба-Дугласа:

Х= F(K, L) = 3K^2/3L^1/3

Определить максимальный выпуск, если на аренду фондов и оплату труда выделено 150 д.е., стоимость аренды единицы фондов w_к= 5 д.е./е.ф., ставка заработной платы w_L = 10 д.е./чел.

Какова предельная норма замены одного занятого фондами в оптимальной точке?

Решение. Поскольку F(0,L) = F(K, 0) = 0, то в оптимальном решении К* > 0, L*>0, поэтому условия (9) принимают вид

 

(10)

 

или в нашем случае

 

 

Поделив первое уравнение на второе, получаем

 

 

Подставив это соотношение в условие w_KK* + w_LL* = 150, находим

 

 

Решение можно проиллюстрировать геометрически. На рис. 1 изображены изокосты (линии постоянных издержек для С = 50, 100, 150) и изокванты (линии постоянных выпусков для Х = 25,2; 37,8).

 

Рисунок 1

 

Изокосты имеют следующие уравнения:

5K+10L=C = const.

Изокванты имеют следующие уравнения:

В оптимальной точке К* = 20, L* = 5 изокванта X* = 37,8 и изокоста, проходящие через эту точку, касаются, поскольку согласно (10) нормали к этим кривым, заданные градиентами , коллинеарны.

Норма замены труда фондами в оптимальной точке

 

 

т.е. один работающий может быть заменен двумя единицами фондов.

Решая задачу фирмы (5) на максимум прибыли, находим единственный оптимальный набор ресурсов х* >0 (рассматриваем случай, когда все ресурсы войдут в набор). Этому набору отвечает единственное значение издержек С* = wx*. Решим теперь задачу (8) на максимум выпуска при заданных издержках С*. Если F(x) — неоклассическая производственная функция, то в оптимальном решении х* > 0, причем это решение единственно.

Таким образом, с одной стороны,

 

,

 

а с другой стороны – . Поскольку П(х^*) = pF(x^*)-wx^* pF()-w =П() и wx^*= w =С^*, то , но , поэтому .

Так как решение задачи на максисмум прибыли (5) единственно, то 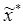= х*. Итак, если задача на максимум прибыли имеет единственное решение х* > 0, то ей отвечает задача на максимум выпуска при заданных издержках С* = wx*, причем последняя имеет такое же решение, как и первая (см. рис. 1).

Геометрическое место точек касания изокост и изоквант при разных значениях издержек С определяет долгосрочный путь развития фирмы Х(С), т.е. показывает, как будет увеличиваться (уменьшаться) выпуск, если издержки возрастут (уменьшатся). Поскольку эта зависимость монотонна, то существует обратная монотонная функция издержек

С = С(Х).

 

Поскольку Х(С) — максимальный выпуск при заданных издержек то издержки С(Х), отвечающие этому максимальному выпуску X, — минимальные издержки.

Если известна функция минимальных издержек С(Х), оптимальный размер выпуска снова определяется из условия максимума прибыли

max П(х), П(х) = рХ -С(X). (11)

Приравниваем к нулю производную:

 

 

т.е. в оптимальной точке предельные издержки равны цене выпуска:

 

 

(кроме того, максимум прибыли достигается при ). Рассмотрим п соотношений (7)

 

Эти соотношения могут быть разрешены относительно х в окрестности оптимальной точки, если якобиан |J| 0, где

 

 

Это означает, что должен быть отличен от нуля гессиан |Н| производственной функции (но Н отрицательно определена, поэтому действительно |Н| =0). Тогда

х* = х* (р,w) (12)

 

или

х_j* = х_j* (р,w), j = 1,…,n

 

Эти п уравнений задают функции спроса (на ресурсы), найденные с помощью модели поведения фирмы. Функции спроса на ресурсы могут быть также найдены экспериментально с помощью методов математической статистики по выборочным данным. Функция предложения

Х*(р, w) = F [x*(p, w)].

 

Подобно уравнениям Слуцкого, показывающим реакцию потребителя на изменения цен товаров, аналогичные уравнения описывают реакцию производителя на изменения цен выпуска и ресурсов.

 

При заданных ценах р, w поведение производителя определяется следующими соотношениями (всего (п + 1) соотношение):

 

Х*(р, w) = F [x*(p, w)],

.

Задачи

1. Производственная функция Х= описывает зависимость между затратами ресурсов х₁, х₂, х₃ и выпуском Х.

Определить максимальный выпуск, если

х₁+х₂+х₃ =9.

 

Каковы предельные продукты в оптимальной точке?

Решение.

Согласно условиям (8) для задачи на максимум выпуска, должны выполняться:

max F(x), wx С, х 0.

 

Составим функцию Лагранжа:

L(x, 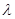) = F(x) + 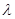(C-wx),

L(x, )= + ;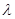

 

Дифференцируя заданную функцию по перменным х₁, х₂, х₃, имеем систему неравенств:

 

Решая систему, получим значения: при 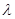= 4,061, 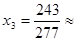0,877.

Обозначим найденую точку через М. Найдем значение функции Х в полученой точке:

 

11,28.

 

Найдем предельные продукты по ресурсам в точке М:

 

 

2. Производственная функция фирмы имеет следующий вид:

Х =3 .

 

Определить предельные продукты по ресурсам и построить изокванту Х =3. Написать уравнеие изоклинали (линии наибольшего роста выпуска), проходящей через точку х₁=1, х₂=1, найти норму замены первого ресурса вторым в этой точке.

Решение.

Предельным продуктом по первому ресурсу является

по второму –

Уравнение изокванты имеет вид при Х =3:

 

х₁

 

 

х₂

 

 

Общее уравнение изоклинали имеет вид: , где (х_{1 0}, х_{2 0}) – координаты точки, через которую проходит изоклиналь. Подставим точки в уравнение, получим: .

Норма замены первого ресурса вторым в этой точке равен:

 

Список используемой литературы

 

1. В. А. Колемаев «Математическая экономика».

2. В. Д. Камаев «Экономическая теория для вузов».

3. В. С. Немчинов «Экономико-математические методы и модели».

4. Ресурс Internet.