Р.А. Каюмов
УДК 624.04 (075)
ББК 38112
© Казанский государственный
архитектурно-строительный
университет, 2012
© Гусев С.В.,2012
ВВЕДЕНИЕ
В методе перемещений в качестве неизвестных принимаются перемещения узлов заданной системы (ЗС).
Идея метода заключается в том, чтобы воспользоваться таблицей 1 готовых решений для построения эпюр моментов. Для этого надо добавить фиктивные связи в узлы системы, чтобы они стали неподвижными. При этом заданная система распадается на однопролетные балки, которые будут воспринимать только те нагрузки, которые приложены непосредственно к ним. Эпюры моментов от этих нагрузок сведены в таблицу 1 стандартных решений. Система с неподвижными узлами называется кинематически определимой. На рис. 5-7 стр. 14-23 приведены три примера, разделы которых соответствуют порядку решения задач методом перемещений. Изучение разделов целесообразно после ознакомления с контрольными вопросами по теме, приведенными в конце методических указаний.
Определение степени кинематической неопределимости заданной системы
Степень кинематической неопределимости определяется по формуле
n = nу + nл, (1)
где nу – число угловых степеней свободы равно числу свободных жестких узлов заданной системы, nл – число линейных степеней свободы узлов.
Для определения nл надо превратить заданную систему в ферму путем введения полных шарниров во все узлы и опорные связи и определить степень свободы ее узлов по формуле:
Wф=2∙У-С-Со,
где У - число узлов фермы, С - число стержней, Со - число опорных связей. Если полученная ферма является механизмом (Wф > 0), то nл равно минимальному числу опорных связей, которые необходимо добавить в узлы фермы, чтобы они стали неподвижными.
Количественная часть кинематического анализа не является достаточным условием для определения числа степеней свободы сооружения. Например, для фермы (рис. 6,б) полученной из заданной системы, Wф = -1. Однако, качественный анализ выявляет одну степень свободы Wф = 1, поскольку данная ферма является мгновенно изменяемой конструкцией (МИК), так как три диска (рис. 6,в): «диск Земля» (фундамент сооружения) и два диска (стержни 1-3 и 3-5) крепятся тремя шарнирами в точках 1, 3, 5, которые лежат на одной прямой. Для превращения ее в кинематически определимую требуется ввести в узел 4 одну горизонтальную опорную связь.
Выбор основной системы (ОС)
Основная система получается из заданной путем введения дополнительных связей в ее узлы, которые обеспечивают их неподвижность. В свободные жесткие узлы добавляют фиктивные заделки, которые лишают их угловой степени свободы. Опорные связи помещают по направлению степеней свободы фермы, полученной из заданной системы. Они лишают все свободные узлы линейных степеней свободы.
В основной системе два вида воздействий: известные активные силы и неизвестные перемещения во вновь введенных связях. В фиктивной заделке неизвестной является ее угол поворота, в опорной связи – ее линейное смещение. Направления неизвестных перемещений, принятые в основной системе, считаются положительными при расчетах и совпадают с положительными направлениями реакций, которые в них возникают в грузовом и единичных состояниях. Число неизвестных Zi равно сумме угловых и линейных степеней свободы nу и nл, определяемых по формуле (1). Основная система с минимальным количеством связей, необходимых для неподвижности узлов, является единственной.
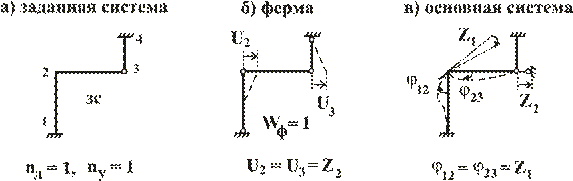
Рис.1
Для уменьшения числа неизвестных Zi используется два предположения. Во-первых, стержни в жестком узле поворачиваются на один и тот же угол (φ12 = φ23 = Z1, рис. 1в), тогда любой свободный жесткий узел обладает только одной угловой степенью свободы. Во-вторых, в стержнях не учитываются деформации растяжения-сжатия и сближение концов стержней после деформации (U2 = U 3 = Z2 , рис. 1в). Основная система (рис. 1в) получается путем внедрения в заданную систему двух связей: фиктивной заделки в узел 2 и горизонтальной опорной связи в узел 3.
Заданная система на рис. 5,а имеет один жесткий узел, следовательно, nу = 1. Все узлы фермы (рис. 5,б), полученной из заданной системы, неподвижны и nл = 0. Основная система получается путем внедрения в жесткий узел 2 фиктивной заделки (рис. 5,в).
В заданной системе на рис. 6,а нет свободных жестких узлов, следовательно, nу = 0. Соответствующая ферма (рис. 6,б) имеет одну степень свободы, поэтому nл = 1. Основная система (рис. 6,г) получается введением в узел 4 горизонтальной опорной связи.
В заданной системе на рис. 7,а один свободный жесткий узел, следовательно, nу = 1. Ферма (рис. 7,б), полученная из заданной системы, имеет одну степень свободы, поэтому nл = 1. Основная система (рис. 7,в) получается путем внедрения в заданную систему двух связей: фиктивной заделки в узел 2 и горизонтальной опорной связи в узел 3.