Лабораторная работа № M-2
ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
НА КРЕСТООБРАЗНОМ МАЯТНИКЕ ОБЕРБЕКА
Цель работы
Целью работы является изучение законов вращательного движения, определение момента инерции J маятника Обербека.
Оборудование и принадлежности
Маятник Обербека, секундомер, набор грузов.
Теоретическая часть
Основные определения и законы динамики вращательного движения
Моментом инерции J материальной точки массой m относительно оси вращения называется величина, равная произведению массы точки на квадрат расстояния её до рассматриваемой оси: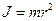 
.
Моментом инерции системы точек (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадрат их расстояний до рассматриваемой оси:
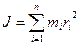. (1)
В случае непрерывного распределения масс эта сумма сводится к интегралу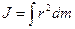 
, где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами x, y, z.
Если известен момент инерции Jс тела относительно оси, проходящей через его центр масс, то момент инерции J относительно любой другой параллельной оси определяется теоремой Штейнера.
Теорема Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции Jс относительно параллельной оси, проходящей через центр масс C тела, сложенному с произведением массы тела на квадрат расстояния а между осями: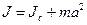 
.
Моментом силы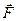 
относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиус-вектора 
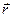, проведенного из точки О в точку А приложения силы, на силу 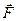. В векторном виде 
.
|
|
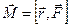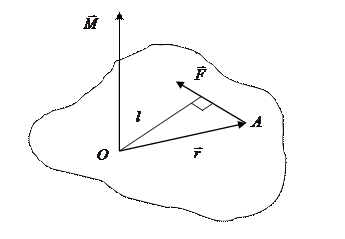
Рисунок 1 – Момент силы
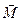- псевдовектор, его направление определяется по правилу правого винта (рисунок 1).
Модуль момента силы
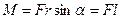. (2)
Здесь α – угол между 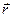и 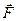, r sinα= l – кратчайшее расстояние между линией действия силы и осью вращения и называется плечом силы.
Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси: сумма моментов сил, действующих на тело относительно оси, равно произведению момента инерции этого тела относительно той же оси на угловое ускорение, приобретаемое телом
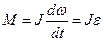, (3)
в векторной форме
.
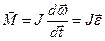Моментом импульса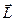 
материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
,
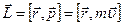где 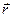- радиус-вектор, проведенный из точки О в точку А;
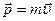- импульс материальной точки.
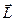- псевдовектор, его направление определяется по правилу правого винта.
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси. Мысленно разобьем это тело на маленькие объемы с элементарными массами mi, находящиеся на расстоянии ri от оси вращения. При вращении эти объемы будут иметь различные линейные
скорости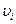 
.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
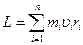. (4)
Скорость поступательного движения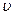 
связана с угловой скоростью ω следующим соотношением: 
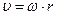. При этом для абсолютно твердого тела угловая скорость вращения составляющих его частиц одинакова.
С учетом этого, используя (1), запишем (4) в виде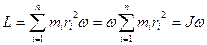 
.
Т.о. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость тела
|
|
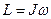. (5)
Продифференцируем уравнение (5) по времени:
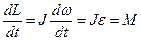. (6)
Т.е. основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси (3) запишется в виде:
,
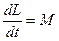- производная момента импульса твердого тела относительно оси вращения равна моменту сил относительно той же оси.
В векторной форме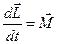 
.
В замкнутой системе момент внешних сил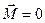 
и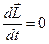 
, откуда
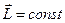или 
, (7)
- это выражение представляет собой закон сохранения момента импульса.
Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Рисунок 2 – Опыт со скамьей Жуковского
Продемонстрировать сохранение момента импульса можно с помощью скамьи Жуковского (рисунок 2). Человек, стоящий на скамье, которая без трения вращается вокруг вертикальной оси, держит в руках гири и вращается с угловой скоростью ω1 . Если человек опустит руки, то его момент инерции уменьшится, в результате чего возрастет угловая скорость ω2 его вращения. Закон сохранения момента импульса для этого опыта: J1ω1=J2ω2.