Маятник Обербека (рисунок 3) состоит из четырех спиц 1 укрепленных на втулке 2 под прямым углом друг к другу. На ту же втулку насажаны два шкива 3 и 4 различных радиусов (r 1 и r2). Вся эта система может свободно вращаться вокруг горизонтальной оси. Момент инерции маятника Обербека можно менять, передвигая грузы 5 вдоль спиц. Момент сил, создается грузом 6 массой m, подвешенным к нити 7, которая навита на один из шкивов и перекинута через блок 8. Под действием момента сил система будет вращаться равноускоренно с постоянным угловым ускорением e. В нерабочем состоянии маятник удерживается от вращения фиксирующим элементом 9. Перемещение груза можно определять по вертикальной шкале 10.
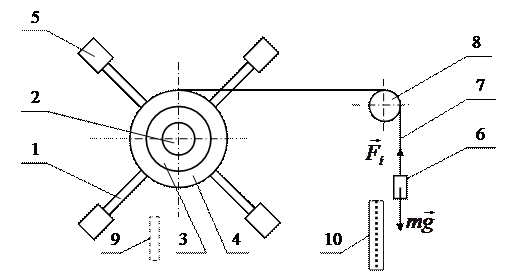
Рисунок 3 – Маятник Обербека
Момента инерции J маятника Обербека можно определить теоретически как сумму моментов инерции составляющих его частей относительно оси вращения согласно (1) или экспериментально, применяя понятия и законы динамики вращательного движения.
Вращение маятника Обербека под действием момента результирующей силы М подчиняется основному уравнению динамики вращательного движения (3).
Груз m движется равноускоренно. Измеряя время t, в течение которого груз m из состояния покоя опустится на расстояние h, можно найти ускорение груза:
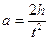. (8)
Угловое ускорение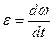 
. Если считать, что нить не проскальзывает по ободу шкива, то ускорение груза будет равно ускорению точек на ободе шкива, а 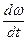= r 
= r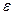 
, отсюда:
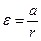, (9)
где r – радиус шкива.
Если через Fн обозначить силу натяжения нити, то момент силы натяжения нити согласно (2) равен:
М н= Fн · r (10)
Силу Fн можно найти из уравнения движения груза:
mg - Fн = ma (11)
Fн = m (g – a) (12)
Момент силы трения Мтр обычно оказывается довольно велик и способен существенно исказить результаты опыта. Поэтому в (3) представим момент силы, действующей на маятник Обербека, как результирующую моментов сил натяжения нити и трения:
|
|
Мн – Мтр =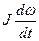 
= 
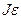(13)
Если вращение равноускоренное и подчиняется уравнению (13), то графически зависимость углового ускорения от момента сил, действующих на систему, будет представлять собой прямую линию, проходящую через точку с координатами [ Мтр; 0] (рисунок 4). Коэффициент пропорциональности и есть искомый момент инерции маятника Обербека:
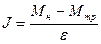(14)
Таким образом, если по экспериментальным значениям удается построить график функции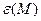 
в виде прямой наклонной линии, то можно говорить о соблюдении основного уравнения динамики вращательного движения (3).
Рисунок 4 – Зависимость углового ускорения от момента сил, действующих на систему
Обратите внимание, что экспериментальные точки вследствие влияния погрешностей измерений могут и не лежать на одной прямой. Поэтому следует провести такую усредненную прямую линию, для которой отклонения точек в обе стороны будут приблизительно одинаковыми. Прямая не пересекает начало координат, так как на систему действует момент силы трения. Если масса m груза, подвешенного на нити, мала, то система может оставаться в равновесии. Другими словами, вращение маятника начнется только тогда, когда момент силы натяжения Мн будет больше момента сил трения Мтр.
4 Порядок выполнения работы
1. Ознакомьтесь с параметрами системы, приведенными в таблице 1.
2. Убедитесь, что нить 7 навита на шкив 4 с бόльшим радиусом r 2 и перекинута через блок 8 (рисунок 3).
|
|
3. Поверните фиксирующий элемент 9 и убедитесь, что маятник может свободно вращаться вокруг горизонтальной оси.
4. Укрепите на нити груз массой m 1 и, осторожно вращая маятник, установите груз так, чтобы его нижний торец находился на отметке «0» на вертикальной шкале 10.
5. С помощью секундомера определите время t 1, за которое груз опустится на расстояние h. Погасите вращение маятника с помощью фиксирующего элемента. Соблюдайте правила техники безопасности!
6. Занесите значение t 1 в таблицу 2.
7. Повторите опыт для этого груза еще два раза, занесите в таблицу 1 значения t 2, t 3.
8. Повторите пункты 1-6 для грузов массами m 2, m 3, m 4, занесите в таблицу 1 результаты измерений.
9. Приведите систему в исходное состояние.
5 Обработка результатов
1. Вычислите среднее арифметическое значение времени движения каждого груза.
2. Для каждого груза по формуле (8) определите ускорение а.
3. Определите угловые ускорения e по формуле (9).
4. Принимая ускорение свободного падения g равным 9,81 м/с2, определите силу натяжения нити Fн (12) и момент этой силы Мн (10). Радиусы шкивов приведены в таблице 1.
5. По расчетным значениям постройте график зависимости 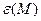. Сравните с рисунком 4. Сделайте вывод о характере вращения и соблюдении уравнения динамики вращательного движения (3).
6. По графику зависимости 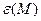определите значение момента сил трения Мтр . Он будет соответствовать точке пересечения прямой с осью абсцисс. Запишите это значение.
7. По формуле (14) определите значение момента инерции J маятника Обербека. Заполните таблицу 2 результатов измерений.
|
|
Таблица 1 - Параметры системы
| Наименование | Значение | |||
| Радиус шкива | r1 = 0,9 см; r2 = 1,75 см | |||
| Перемещение груза | h =1 м | |||
| Абсолютные погрешности прямых измерений | Δ m =0,1г; Δ t =0,01c; Δ h =0,005м | |||
Таблица 2 – Результаты измерений
| N опыта | m, кг | t, с | a, м/с2 | e, 1/с2 | Fн, Н | Мн, Н×м | J, кг×м2 | |||
| t 1 | t 2 | t3 | tср | |||||||
8. Определите среднее значение момента инерции Jср маятника Обербека.
9. Определите относительные погрешности прямых измерений xh, xt и xm, зная, что относительная погрешность величины Х
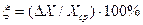
10. По наибольшей величине xmax определите абсолютную погрешность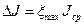 
.
11. Представьте ответ в виде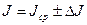 
, кг×м2 .
6 Контрольные вопросы
1. Что называется моментом инерции материальной точки, тела (системы материальных точек) относительно оси вращения?
2. От чего зависит момент инерции маятника Обербека в данной работе?
3. Изменится ли момент инерции маятника Обербека в данной работе при изменении радиуса шкива?
4. Основное уравнение динамики вращения тела вокруг неподвижной оси.
5. Сформулируйте закон сохранения момента импульса. Приведите примеры.
6. Решите приведенные ниже тестовые задания.
Задание 1
| Три маленьких шарика расположены в вершинах правильного треугольника. Момент инерции этой систем относительно оси О 1, перпендикулярной плоскости треугольника и проходящей через его центр – J 1. Момент инерции этой же системы относительно оси О 2, проходящей через один из шариков – J 2. Справедливо утверждение… o J 1 > J 2 o J 1 = J 2 o J 1 < J 2 |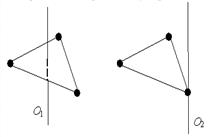 
|
Задание 2
| Из жести вырезали три одинаковые фигуры в виде эллипса. Две детали разрезали вдоль разных осей симметрии. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO′. Для моментов инерции относительно оси OO′ справедливо соотношение… o J1 = J2<J3 o J1 < J2=J3 o J1 > J2>J3 o J1 < J2<J3 |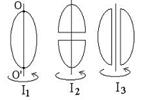 
|
Задание 3
| К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр диска О перпендикулярно плоскости рисунка, то плечо силы F 3 равно… o а o b o c o 0 |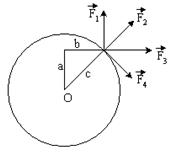 
|
Задание 4
Если момент инерции тела увеличить в 2 раза и скорость его вращения увеличить в 2 раза, то момент импульса тела…
o Увеличится в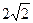 
раз
o Не изменится
o Увеличится в 4 раза
o Увеличится в 8 раз
Задание 5
Человек сидит в центре вращающейся по инерции вокруг вертикальной оси карусели и держит в руках горизонтально длинный шест за его середину. Если человек повернет шест вертикально, то частота вращения карусели в конечном состоянии…
o Не изменится
o Уменьшится
o Увеличится
Задание 6
Момент импульса тела относительно неподвижной оси изменяется по закону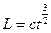 
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
| o |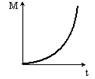 
| o |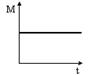 
|
| o |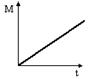 
| o |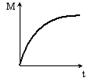 
|
Задание 7
| Диск вращается равномерно с некоторой угловой скоростью w. Начиная с момента времени t=0, на него действует момент сил, график временной зависимости которого представлен на рисунке. Укажите график, правильно отражающий зависимость момента импульса диска от времени. |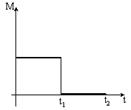 
| ||||
| o |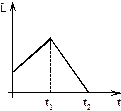 
| o |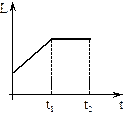 
| ||
| o |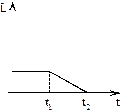 
| o | 
| ||