Астраханский Государственный Технический Университет
кафедра физики
Лабораторная работа
по физике:
«Определение ускорения свободного падения
Для Астрахани
При помощи оборотного маятника».
Выполнил:
Ст.гр.ДТЕТ 11/2б
Козлов А.
Проверил:
Ст.преподаватель
Березина И.С.
астрахань – 2013 г.
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫТЯЖЕСТИ ПРИ ПОМОЩИ
ОБОРОТНОГО МАЯТНИКА
Цель работы: измерить ускорение силы тяжести для Астрахани.
Оборудование: оборотный маятник, секундомер.
Краткая теория.
Классическую нерелятивистскую теорию гравитации создал И. Ньютон в 1678 году. Он установил закон всемирного тяготения, согласно которому две материальные точки с массами m1 и m2 притягивают друг друга с силой, пропорциональной произведению масс этих точек и обратно пропорциональной квадрату расстояния r между ними:
. (2.1)
В векторной форме будем иметь:
. (2.2)
Здесь F1,2 – сила, действующая на первую материальную точку со стороны второй, r – радиус-вектор, направленный от первой материальной точки ко второй. Сила F2,1 отличается от силы F1,2 только знаком: 
.
Коэффициент пропорциональности G называют гравитационной постоянной или постоянной тяготения. Общепринятое значение G:
G = 6,67 * 10 –11 
.
Сила, с которой два тела притягиваются друг к другу, называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены вдоль одной прямой, проходящей через центры взаимодействующих тел. Гравитационное взаимодействие является фундаментальным. Важно также, что формулы (2.1) и (2.2) справедливы только для материальных точек.
На любое тело, расположенное вблизи Земли, действует гравитационная сила F, под влиянием которой, согласно второму закону Ньютона, тело начинает двигаться с ускорением свободного падения g, то есть в системе отсчета, связанной с Землей, на всякое тело массой m действует сила, равная:
, (2.3)
называемая силой тяжести.
Согласно фундаментальному физическому закону, обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Следовательно, в данном месте Земли ускорение свободного падения одинаково для всех тел. Его изменение в разных точках пространства обусловлено суточным вращением Земли вокруг своей оси, а так же её формой и неоднородностью.
Если пренебречь суточным вращением Земли вокруг своей оси, то сила тяжести и сила тяготения равны между собой:
, (2.4)
где М – масса Земли, R0 – радиус Земли, h – расстояние от поверхности Земли до тела. Из формулы следует, что
, (2.5)
то есть g зависит только от массы Земли и расстояния между телом и земной поверхностью. Важным следствием этой формулы является также то, что g не зависит от массы тел.
Состояние тела, при котором оно движется только под действием силы тяжести, называется свободным падением.
Гравитационное взаимодействие между телами осуществляется посредством поля тяготения (гравитационного поля). Это поле порождается телами и является одной из форм материи.
Для силовой характеристики гравитационного поля вводится векторная величина
, (2.6)
где F – сила, действующая в данной точке поля на тело массой m. Эта величина называется напряженностью гравитационного поля. Можно говорить, что ускорение свободного падения и напряженность гравитационного поля одна и та же величина.
Величину
, (2.7)
где Ep – потенциальная энергия, которой обладает тело массы m в данной точке поля, называют потенциалом гравитационного поля.
Связь между напряженностью и потенциалом гравитационного поля устанавливает соотношение:
. (2.8)
В физике всякое твёрдое тело, колеблющееся под действием силы тяжести вокруг неподвижной точки или оси, называют маятником.
Физический маятник определяют как тело, укреплённое на неподвижной горизонтальной соединяющей точку подвеса О и центр тяжести С (рис.2.1).
При отклонении маятника от положения равновесия возникает момент М силы тяжести, стремящийся вернуть маятник в положение равновесия. Этот момент равен:
M = - m g l sinj (2.9)
| где m – масса маятника, l – расстояние между точкой подвеса и центром тяжести C. Момент М имеет такое направление, что стремится уменьшить угол отклонения j. Поэтому в соотношении (2.9) стоит знак минус. Для отыскания закона движения маятника воспользуемся основным уравнением динамики вращательного движения:
 , (2.10)
где I – момент инерции тела относительно оси, проходящей через точку О; e - угловое ускорение, численно равное:
|
.
Момент сил трения для простоты расчетов не учитываем.
Подставив в этот закон соотношение (2.9), получаем уравнение движения маятника в дифференциальной форме:
- m g l sinj. (2.11)
В случае малых углов при отклонении маятника sinj » j, тогда уравнение (2.11) можно записать в упрощённой форме:
m g lj. (2.12)
Решение этого уравнения имеет вид:
, (2.13)
где 
- циклическая частота.
Зная, что
получаем для периода колебаний физического маятника:
. (2.14)
Частным случаем физического маятника является математический маятник.
| Математическим маятником называется система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити. Момент инерции математического материальной точки относительно точки О равен:
 . (2.15)
Подставив в формулу (2.14) выражение (2.15) получим, что период колебаний математического маятника равен:
 . (2.16)
Из сопоставления формул (2.14) и (2.16) получается, что физический маятник име ет тот же период колебаний, что и математический с длиной:
|
. (2.17)
Выражение I / ml называют приведённой длиной физического маятника. lпр – эта длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.
На практике приведённая длина физического маятника определяется расстоянием между точкой подвеса маятника О и его центром качания О’, если периоды колебаний на обеих призмах совпадают (рис.2.1). Точка на прямой, соединяющая точку подвеса с центром тяжести на расстоянии приведённой длины от вращения называется центром качания физического маятника. Точка подвеса О и центр качания О’ обладают свойством взаимности. Если подвесить физический маятник в точке O’, а прежняя точка подвеса станет центром качания то приведённая длина, а значит и период колебаний маятника не изменится.
На этом свойстве основано определение ускорения свободного падения с помощью оборотного маятника. Оборотным маятником называется маятник, у которого имеются параллельные закреплённые вблизи его концов опорные призмы П1 и П2, на которых он может совершать колебания, опираясь на ребро той или иной призмы (рис.2.3). Вдоль маятника может перемещаться закреплённый на нём груз Г1. Перемещением этого груза можно установить такое положение центра тяжести маятника, что при подвешивании его на любую из призм период колебаний останется одинаков. Тогда расстояние между опорными призмами составит lпр. Измерив период колебаний маятника и зная его приведённую длину, можно по формуле:
(2.18)
определить ускорение свободного падения:
.
Так как оборотный маятник – частный случай физического маятника, то необходимо решить вопрос: когда же физический маятник можно считать оборотным?
Основное свойство оборотного маятника состоит в том, что центр вращения (точка О) и центр качаний (точка О') взаимозаменяемы.
Рассмотрим три возможных соотношения между длиной l и приведенной длиной lпр физического маятника:
1) 
;
;
;
,
что невозможно, так как величины I, m, l по сути своей положительные. При таком соотношении между l и lпр маятник будет переворачиваться, так как центр тяжести оказывается выше точки подвеса и тело находится в положении неустойчивого равновесия.
2) 
;
;
;
;
,
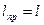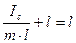то есть тело будет находиться в состоянии покоя.
3) 
;
;
;
,
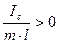то есть только в этом случае будут происходить колебания.
Порядок выполнения работы.
1. Поставим груз Г1 в положение 1 на шкале маятника.
2. Отклонив маятник на угол не более 10°, замерим t1 – время 25 полных колебаний на опорной призме П1.
3. Перевернём маятник и замерим t2 – время 25 полных колебаний на опорной призме П2.
4. Повторим 2 и 3 пункты для случаев, когда груз Г1 находится в положениях 2, 3, 4, 5 шкалы маятника.
5. Результат заносим в таблицу № 1.
Таблица № 1
| № п/п | Деления шкалы, см | N – число колебаний | t1 c | T1 c | t2 c | T2 c |
где, T1 – период колебаний маятника на призме П1, T2 – период колебаний маятника на призме П2.
6. Считаем 
и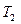 
по формуле T = t / n.
7. По табличным данным строим график зависимости и 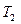от положения груза Г1 на шкале маятника. Если пересечение двух графиков не произошло или точек пересечения несколько, то работа выполнена неверно.
|
8. Из пересечения кривых на графике находим Т0 – период, одинаковый для колебаний маятника на призмах П1 и П2.
9. Ставим подвижный груз в положение Х, соответствующее пересечению кривых на графике и измеряем периоды колебаний на одной и второй призме 
(число колебаний не менее 50).
10. Исходя из полученных значений 
, , найти среднее значение периода колебаний (Тср).
11. Вычислить среднюю абсолютную ошибку в определении периода (D Тср).
12. Найти относительную ошибку в определении периода (dT,%).
13. Вычислить среднее значение ускорения свободного падения по формуле:
Найти относительную ошибку в определении ускорения свободного падения, исходя из относительной ошибки периода:
.
14. Найти среднюю абсолютную ошибку ускорения свободного падения:
.
15. Записать ответ в виде
Правила техники безопасности.
1. Угол отклонения маятника от вертикального положения не должен превышать 5-10°.
2. Следить, чтобы во время выполнения работы ребро призмы маятника не соскальзывало с опоры кронштейна.
Контрольные вопросы.
1. Закон всемирного тяготения. Гравитационная сила.
2. Сила тяжести. Ускорение силы тяжести.
3. Гравитационное поле. Основные характеристики гравитационного поля.
4. Что представляют собой математический, физический и оборотный маятники?
5. Составить дифференциальные уравнения движения маятников. Записать их решения. Сделать анализ решения.
6. Получить расчетную формулу для определения ускорения свободного падения.
7. Объяснить физический смысл величины g.
8. Назвать основные этапы выполнения работы и правила техники безопасности при этом
объяснить:
а) расчет искомых величин;
б) нахождение ошибок в определении этих величин.
9. Что такое приведённая длина для физического и оборотного маятника?
10.Какой знак нужно поставить между l и lпр для физического маятника, чтобы его можно было считать оборотным? (Рассмотреть с точки зрения теории равновесия).
Литература.
1. И. В. Савельев. Курс общей физики. I том.
2. Д. В. Сивухин. Общий курс физики.
3. Г. А. Зисман, О. М. Тодес. Курс физики. I том.
4. А. Ф. Сорокин, М. И. Сурков, С. А. Кушкин. Методические рекомендации по курсу физики. 1997 г.