Неравенства.
Решение неравенств и систем неравенств
Линейное неравенство.
Линейным неравенством называется неравенство вида:
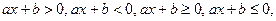 где a и b – действительные числа,
где a и b – действительные числа, 
Решить неравенство – значит найти все значения переменной, при которых неравенство обращается в верное числовое неравенство.
При решении неравенств используются их свойства:
1) Если а > b то b < а.
2) Если а > b и b > c, то а > с.
3) Если а > b и с – любое число, то а + с > b +с
4) Если а > b и с > 0, то ас > bc;
если а > b и с < 0, то ас < bc.
Пример 1.
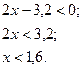
Ответ: 
Пример 2.
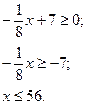
Ответ: 
Пример 3.
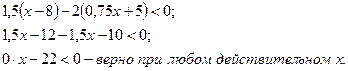
Ответ: 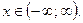
Пример 4.

Ответ: нет решения.
Система линейных неравенств.
Решением системы линейных неравенств называется пересечение множеств решений этих неравенств, т.е. те значения переменной, которые одновременно удовлетворяют всем неравенствам системы.
Пример 1.
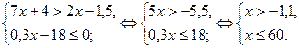
На числовой прямой решение каждого неравенства показывают штриховкой соответствующего числового промежутка, тогда решение системы – пересечение заштрихованных промежутков:
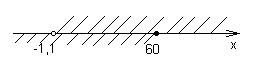
Ответ: 
Пример 2.
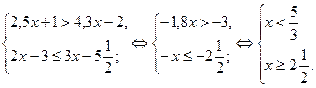

Ответ: нет решений.
Неравенства с модулем.
Пример 1.
Решите неравенство 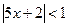
Решение:
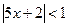 Û
Û 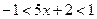 Û
Û
Û 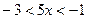 Û
Û
Û  .
.
Ответ: 
Пример 2.
Решите неравенство 
Решение:
 Û
Û 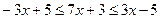
Перейдем к системе неравенств.
 Û
Û  Û
Û 
Найдем решение системы. Для этого покажем на числовой прямой решения обоих неравенств системы и найдем пересечение этих множеств.

Данные множества не пересеклись.
Ответ: решений нет.
Пример 3. Решите неравенство 
Решение:  Û
Û  Û
Û 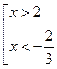
Ответ: 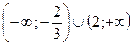
Квадратные неравенства.
Неравенство вида 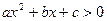 или
или 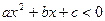 , где
, где 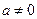 , называется квадратным неравенством.
, называется квадратным неравенством.
Выражение слева от знака неравенства можно рассматривать как квадратичную функцию, тогда решение исходного неравенства сводится к нахождению промежутков знакопостоянства соответствующей квадратичной функции (т.е. промежутков, на которых значения функции положительны или отрицательны).
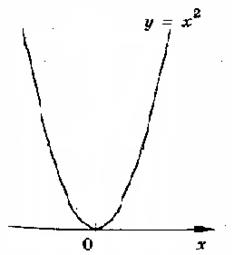
Пример 1. 
Парабола  расположена выше оси
расположена выше оси  при любом
при любом  .
.
Ответ: 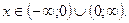
Пример 2. 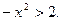
Так как 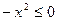 при любом действительном значении x, то неравенство не имеет решений.
при любом действительном значении x, то неравенство не имеет решений.
Пример 3.
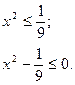
Решение. Изобразим схематично график функции 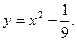 Для этого найдем нули функции (т.е. точки, в которых y = 0).
Для этого найдем нули функции (т.е. точки, в которых y = 0).

Ветви параболы направлены вверх, так как a = 1 > 0.
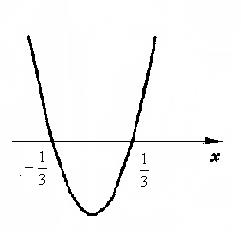
Неравенство  выполняется при
выполняется при  Концы промежутка включаются, так как задано нестрогое неравенство.
Концы промежутка включаются, так как задано нестрогое неравенство.
Ответ: 
Пример 4. 
Решение. Рассмотрим функцию  Построим эскиз параболы.
Построим эскиз параболы.
Ветви параболы направлены вниз, так как a < 0. Найдем точки пересечения параболы с осью  :
:

По эскизу найдем решение неравенства 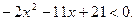

Ответ: 
Решение неравенств методом интервалов.
Пример 1. (x + 5)(x – 1)x > 0.
Решение. Отметим на числовой прямой все точки, в которых левая часть данного неравенства обращается в 0. Эти точки разбивают числовую прямую на промежутки. Найдем знак произведения в левой части неравенства на каждом промежутке.
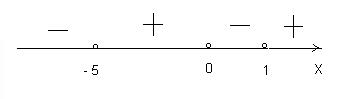
При x > 1 каждый множитель произведения положителен, следовательно, их произведение также будет положительным (что отмечается знаком “+” над соответствующим промежутком).
При 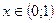 второй множитель становится отрицательным, другие же множители остаются положительными, следовательно, произведение будет отрицательным.
второй множитель становится отрицательным, другие же множители остаются положительными, следовательно, произведение будет отрицательным.
Аналогично определим знаки произведения на промежутках 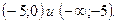
Решение неравенства – объединение промежутков, на которых значение произведения в левой части данного неравенства положительно.
Ответ: 
Пример 2. 
Решение. Разложим квадратный трёхчлен в левой части неравенства на множители, пользуясь теоремой Виета:
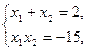 Û
Û 
 .
.
Далее решение неравенства будет аналогично приведённому выше. Записываем ответ с учётом того, что данное неравенство нестрогое (т.е. включая концы промежутков).
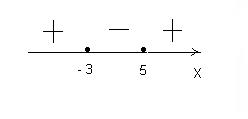
Ответ: 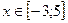 .
.
Пример 3. 
Решение. Отметим на числовой прямой точки, в которых левая часть неравенства обращается в нуль.
Отметим, что если степень выражения чётная, то значение выражения неотрицательно и, следовательно, знак всего произведения зависит от выражений, возведённых в нечётную степень.
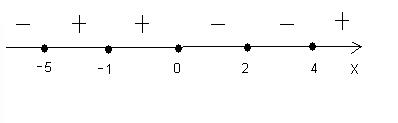
Ответ:  .
.
Число 2 включено в ответ, так как значение выражения в этой точке равно 0.
Пример 4. Решите неравенство 
Решение.
Вынесем в знаменателе за скобки -1.
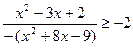
Умножим обе части неравенства на -1.

Перенесем 2 в правую часть неравенства и заметим, что х = 1 является корнем как числителя, так и знаменателя. Поэтому сразу разложим числитель и знаменатель на множители.
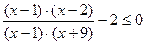
Сократим дробь на ( ), не забыв ограничение.
), не забыв ограничение.
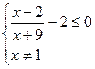
Приведем слагаемые к общему знаменателю.

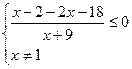
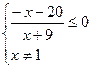
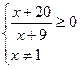
Решим первое неравенство на числовой прямой.

Учтем второе неравенство системы.

Ответ: 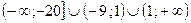
Пример 5. Решите неравенство: 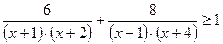
Решение: В знаменателях раскроем скобки.

Выполним замену переменных.
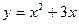
Получим:
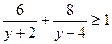

Приведем все слагаемые к общему знаменателю.

Упростим числитель дроби.

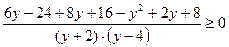

Умножим обе части неравенства на -1.


Вернемся к прежней переменной.

Разложим все квадратные трехчлены на множители.
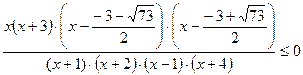
Оценим дробь 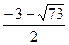
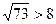
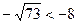


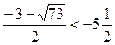
Оценим дробь 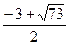
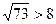
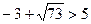
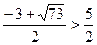
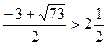
Решим неравенство методом интервалов.
 x
x
 -4 -3 -2 -1 0 1
-4 -3 -2 -1 0 1 
Ответ: 