Определения
Элементарная струйка – струйка жидкости, боковая поверхность которой образована линией тока, проходящей через бесконечно малый замкнутый контур. Распределение скоростей по поперечному сечению элементарной струйки считается равномерным, по причине малости площади поперечного сечения, поэтому коэффициент Кориолиса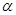 
равен единице.
Идеальная жидкость – модель жидкости, применяемая для расчётов реальных гидродинамических процессов.
Для идеальной жидкости приняты следующие допущения:
· отсутствуют касательные напряжения между слоями жидкости, следовательно,
отсутствует вязкость жидкости, следовательно, отсутствует трение между слоями жидкости, следовательно, в жидкости отсутствуют потери напора;
· жидкость является не сжимаемой;
· в жидкости отсутствует теплопроводность, т.е. жидкость не изменяет свой объём при изменении температуры;
· поток жидкости является сплошным, т.е. в жидкости отсутствуют места пустот или переуплотнений.
Виды уравнения Бернулли
Для элементарной струйки идеальной жидкости
Для элементарной струйки коэффициент Кориолиса равен единице, в идеальной жидкости отсутствуют потери, поэтому уравнение Бернулли будет иметь вид:
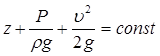(1)
Для потока реальной жидкости
Для потока жидкости коэффициент Кориолиса будет иметь значение отличное от единицы, и зависеть от режима течения, для ламинарного режима α = 2, для турбулентного режима α = 1,05-1,1. Реальная жидкость имеет вязкость, следовательно, в реальной жидкости будут потери напора, поэтому уравнение Бернулли будет иметь вид:
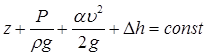
Геометрический смысл уравнения Бернулли
Рассмотрим уравнение Бернулли для элементарной струйки идеальной жидкости (1).
В уравнении (1) все три слагаемых имеют линейную размерность [м]. Соответственно каждую высоту можно представить в виде реальных отрезков:
геометрическая высота, представляет собой расстояние от оси элементарной струйки (трубопровода) до поверхности земли.
пьезометрическая высота, показывает на какую высоту, может подняться жидкость под действием избыточного давления в данной точке, при условии, что на свободную поверхность действует давление внешней газообразной среды (т.е. атмосферное давление).
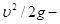скоростная высота, показывает высоту, при падении с которой, частица жидкости достигла бы скорости 
.
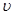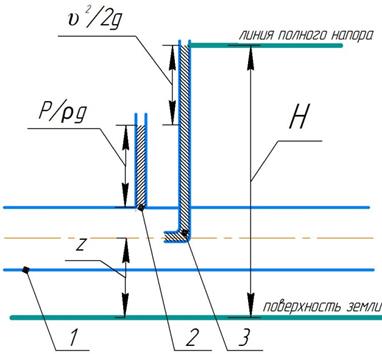
Рис. 1 Иллюстрация геометрического смысла уравнения Бернулли.
1 – элементарная струйка; 2 – пьезометр; 3 – трубка Пито (прибор для измерения скоростной высоты).
Геометрический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх слагаемых уравнения Бернулли остаётся величиной постоянной и равной величине полного напора Н [м].
(2)
Энергетический смысл уравнения Бернулли
Умножим каждое слагаемое уравнения (2) на величину ускорения свободного падения:
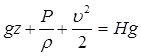
В итоге получаем слагаемые, который можно описать с точки зрения энергии:
где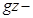 
удельная потенциальная энергия положения, т.е. если поднять жидкость массой 1 кг на высоту 
, то она будет иметь потенциальную энергию 
;
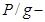удельная потенциальная энергия давления;
удельная кинетическая энергия;
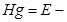полная удельная механическая энергия элементарной струйки.
Энергетический смысл уравнения Бернулли заключается в следующем: по длине элементарной струйки сумма трёх удельных энергий остаётся величиной постоянной и равной величине полной удельной механической энергии Е [Дж]. Возможна и другая формулировка: уравнение Бернулли – это есть закон сохранения энергии для элементарной струйки (потока) жидкости, который отображает взаимный переход кинетической и потенциальной энергии.
Потери
В потоке реальной жидкости в уравнение Бернулли добавляется слагаемое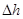 
, которое
представляет собой величину потерь напора. Запишем уравнение Бернулли для двух произвольных сечений потока жидкости:
С геометрической точки зрения потери отображаются отрезком, расположенным над скоростным напором, при этом потери отображаются во втором сечении.
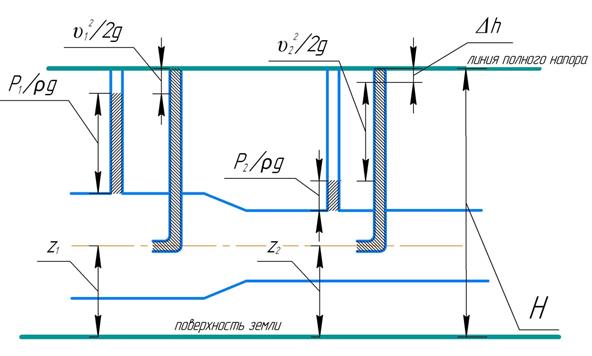
Рис. 2. Иллюстрация потерь напора.
С энергетической точки зрения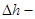 
это величина, показывающая, сколько энергии жидкость тратит на преодоление различных сопротивлений при переходе из первого сечения во второе сечение.
6. Порядок проведения расчётов:
1. Определить величину расхода жидкости:
2. Поскольку диаметры d1=d3, дальнейшие расчёты для широких частей трубопровода будут одинаковы. Поэтому будем проводить расчёт для одной широкой части трубопровода, при этом параметры жидкости, обозначая через индекс 1-3
Определить площади поперечного сечения трубопроводов S1-3, S2 [м];
3. Определить скорость течения жидкости:
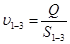
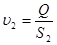
4. Определить режим течения жидкости:
5. Определить величины скоростного напора: 
; 
6. На листе А4 построить график, зависимости изменения пьезометрического напора от
длины сечения трубопровода.По оси Х откладываются расстояния между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см
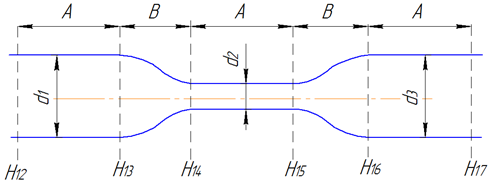
Рис. 3 Условное изображение исследуемого
трубопровода с точками подключения пьезометров.
По оси Y откладываются показания соответствующих пьезометров. В результате получится шесть точек, который соединяются ломаной линией. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.
7. На листе А4 построить график, зависимость изменения скоростного напора от длины
сечения трубопровода.По оси Х откладывается расстояние между точками, к которым подключены пьезометры. Расстояния равны: А=25см, В=12,5 см.
По оси Y откладываются значения скоростного напора. Поскольку экспериментальные исследования проводились для трёх различных случаев, поэтому в результате мы имеем три графика в одной системе координат.
8. Вывод о работе с описанием графиков
Таблица 1. Результаты опыта
| № | V [л] | ∆t [сек] | НП12 [мм] | НП13 [мм] | НП14 [мм] | НП15 [мм] | НП16 [мм] | НП17 [мм] |