ОБЩИЕ ТРЕБОВАНИЯ ПО выполнению практических Заданий

Автономная некоммерческая профессиональная образовательная организация

«УРАЛЬСКИЙ ПРОМЫШЛЕННО-ЭКОНОМИЧЕСКИЙ ТЕХНИКУМ»

 

Сборник методических указаний

По выполнению заданий на практических занятиях

по дисциплине «Теоретические основы теплотехники и гидравлики»

по разделам 1 «Основы технической термодинамики»

и 2 «Основы теплопередачи»

по специальности 13.02.02

«Теплоснабжение и теплотехническое оборудование»

для студентов заочного отделения 1 курса

 

Рассмотрен и одобрен на Составлен в соответствии с

заседании цикловой комиссии рабочей программой к

теплотехнических дисциплин уровню подготовки выпуск- ников по специальности

13.02.02

«______»______________2014г.

 

Председатель_________Н.В.Панова

 

 

Утверждено

Методическим советом «УПЭТ»

Протокол №______от____________2014г.

 

 

Председатель_____________Н.Б.Чмель,зам. директора АН ПОО

«УПЭТ» по УР

 

Составитель:___________ Н.В.Барихина, преподаватель АН ПОО «УПЭТ»

 

 

Рецензент:______________Н.В.Панова, преподаватель АН ПОО «УПЭТ»

 

СОДЕРЖАНИЕ

 

Введение 4

ОБЩИЕ ТРЕБОВАНИЯ ПОВЫПОЛНЕНИЮ

ПРАКТИЧЕСКИХ ЗАДАНИЙ 7

1 ПрактическОЕ ЗАДАНИЕ

Тема: Параметры состояния тела 8

2 ПрактическОЕ ЗАДАНИЕ

Тема: Основные термодинамические процессы 13

3 ПрактическОЕ ЗАДАНИЕ

Тема: Нахождение параметров водяного пара по h-S диаграмме 26

4 ПрактическОЕ ЗАДАНИЕ

Тема: Теплопередача 32

5 ПрактическОЕ ЗАДАНИЕ

Тема: Теплообменные аппараты 47

Приложения 59

СПИСОК ЛитературЫ66

 

 

Введение

Целью методических указаний является оказание помощи студентам при подготовке и выполнении практических заданий по разделам 1 «Основы технической термодинамики» и 2 «Основы теплопередачи» по дисциплине «Теоретические основы теплотехники и гидравлики».

Данные методические указания предназначены для студентов 1 курса заочного отделения по специальности 13.02.02 «Теплоснабжение и теплотехническое оборудование» с целью научить студентов применять полученные на аудиторных занятиях знания по теории теплотехники при решении практических задач, включающие в себя пять практических заданий. В результате усвоения теоретического материала и проведения конкретных расчетов студенты получают определенные навыки для дальнейшего изучения общепрофессиональных дисциплин и профессиональных модулей.

Практические задания способствуют формированию общих компетенций:

ОК 1 Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес;

ОК 2 Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество;

ОК 4 Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития;

ОК 5 Использовать информационно-коммуникационные технологии в профессиональной деятельности;

ОК 6 Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями;

ОК 7 Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

Выполнение студентами практических заданий направлено на:

- обобщение, систематизацию, углубление, закрепление получен­ных теоретических знаний;

- формирование умений применять полученные знания на практике, реализацию единства интеллектуальной и практической деятельности;

- формирование профессио­нально значимых качеств, как самостоятельность, ответственность, точность, коллегиальность, творческая инициатива.

В ходе выполнения заданий на практических занятиях, студенты овладевают первоначаль­ными профессиональными умениями:

- пользоваться справочной литературой;

- переводить единицы измерения давления в разные системы.

Формы организации студентов на прак­тических занятиях: фронтальная и индивидуальная.

Формы и методы контроля и оценки - оценка результатов выполнения практического задания

Критерии оценки:

5 – «отлично» - задание выполнено в полном объёме с соблюдением необходимой последовательности. Студент работает самостоятельно: подбирает необходимые для выполнения задания источники знаний, показывает необходимые для выполнения практического задания теоретические знания и практические умения, расчёты произведены правильно, отчёт по практическому занятию сдан в соответствии с графиком учебного процесса;

4 – «хорошо» - задание выполняется студентом самостоятельно в полном объёме. Допускаются отклонения от необходимой последовательности выполнения, не влияющие на правильность конечного результата, использует указанные источники знаний, работа студента показывает знание им основного теоретического материала и овладение умениями, необходимыми для самостоятельного выполнения задания. Допускаются неточности и неаккуратность в оформлении результатов работы, не у всех искомых параметров правильно проставлены единицы измерения, имеются незначительные описки и орфографические ошибки;

3 – «удовлетворительно» - практическое задание выполняется и оформляется студентом при помощи преподавателя. На выполнение задания затрачивается много времени с учётом самостоятельной работы студента во внеаудиторной деятельности. Студент показывает знания теоретического материала, но испытывает затруднения при самостоятельной работе со справочной и учебно-методической литературой, в отчёте во множественном числе встречаются технические, математические и орфографические ошибки, отчёт по практическому занятию сдан не в соответствии с графиком учебного процесса;

2 – «неудовлетворительно» - студент не подготовлен к выполнению задания. Полученные результаты не соответствуют реальным показателям. Студент показывает плохое знание теоретического материала и отсутствие необходимых умений. Руководство и помощь со стороны преподавателя и хорошо подготовленных студентов неэффективны по причине неудовлетворительной подготовки студента.

 

ОБЩИЕ ТРЕБОВАНИЯ ПО выполнению практических Заданий

 

1. Исходные данные для выполнения задания берутся из приложения А в соответствии с номером своего варианта. Выбор номера варианта
производится по первоначальному списку в журнале при изучении данной темы.

2. Отчёт по выполненному заданию сдается в установленный срок.

3. При оформлении задания необходимо учесть следующие основные
требования:

· задания выполняются в печатном варианте на листах форматом А4;

· оформление задания производится 14 шрифтом полуторным интервалом;

· рассчитываемые формулы даются с пояснениями;

· расчёты к формулам не приравниваются;

· размерности рассчитываемых величин указываются в системе СИ;

· задания оформляются аккуратно, допускается при исправлениях пользоваться штрих - корректором;

· после выполнения задания приводится список используемой
литературы.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

Тема: Параметры состояния тела

Цель работы: Формирование уменийпо переводу единиц измерения

термодинамических параметров

Формируемые компетенции: ОК2, ОК4, ОК5

Ресурсы:

1. Барихина Н.В. Методические указания по выполнению заданий на практических занятиях [Текст]: - Екатеринбург: УПЭТ, 2013.-55с.

2. Бахшиева Л.Т., Кондрауров Б.П. [и др.] Техническая термодинамика и теплотехника: учебное пособие для вузов [Текст]: - М.: Изд. центр "Академия", 2008.-345с.

3. Прибытков И.А. Теоретические основы теплотехники: учеб. для студентов учреждений среднего профессионального образования[Текст]: – М.: Изд. центр "Академия", 2004.-276с.

Задание:

· ознакомиться с общими сведениями;

· выполнить задания №1,2 и 3;

· ответить на контрольные вопросы.

Общие сведения:

 

Величины, характеризующие тело в данном состоянии, называются параметрами состояния: удельным объёмом, давлением и температурой.

1. Удельный объём тела v представляет собой объём единицы его массы и измеряется в м³/кг. В технической термодинамике за единицу массы принимают килограмм (кг), за единицу объёма - кубический метр (м³).

v = V/m (1.1)

Величина, обратная удельному объему, называется плотностью ρ и измеряется в кг/м³ и представляет собой массу единицы объема.

ρ = 1/v (1.2)

Уравнение (1.2) позволяет определить плотность газа при любых условиях, если известно его значение для определённых условий.

Таблица 1.1 - Атомные массы химических элементов

Элемент	Обозначение	Атомная масса
Водород	Н
Гелий	Не
Углерод	С
Азот	N
Кислород	О
Сера	S
Хлор	Сl

 

Таблица 1.2 - Химическая формула газов

Название	Химическая формула	Название	Химическая формула
Водород	Н2	Водная пара	Н2О
Кислород	О2	Аммиак	NН4
Азот	N2	Ацетилен	С2Н2
Окись углерода	СО	Метан	СН4
Углекислый газ	СО2	Бензол	С6Н6

2. Давление Р измеряется силой, приходящейся на единицу поверхности. Во всех термодинамических уравнениях пользуются единицей измерения Паскаль

1Па=1 Н/м²,

1бар = 10⁵Н/м².

В технической системе за единицу силы принимают килограмм силы (кгс), который равен 9,80665 ньютона, а за единицу давления - килограмм силы на квадратный сантиметр (кгс/м²),т.е.

1 ат = 10⁴ · 9,81 Н/м² = 0,981 бар

Давление так же можно измерять высотой столба жидкости (ртути или воды).

· Техническая атмосфера соответствует 735,6 мм рт. ст. при температуре ртути 0° С или 10 м вод. ст.

· Физическая атмосфера (атм) соответствует 760 мм рт. ст. при температуре воды ОºС или 10332 мм вод. ст.

· 1 ат = 1 кгс/см² = 10 00 кгс/м² = 735,6 мм рт. ст. = 10 000 мм вод. ст. =

= 0,981бар

· 1 атм =1,0332 кгс/см² =10 332 мм вод.ст.=760 мм рт.ст.=

=10332 вод.ст.=1,013 бар;

· 1 кГ/м² = 1 мм вод. ст. = 9,81 Н/м².

Манометры служат для измерения давления выше атмосферного. Их показания дают избыток давления измерения среды над атмосферой давлением - манометрическое (Р_ман ), или избыточное (Р_изб) давление.

Абсолютное давление определяется из соотношения:

Р_абс = Р_изб + В, (1.3)

где В - атмосферное или барометрическое давление.

Вакуумметры служат для измерения давления ниже атмосферного,

которое называется вакуумом или разрежением. По их показаниям судят насколько давление рассматриваемой среды меньше атмосферного.

Абсолютное давление в этом случае определяется из равенства:

Р_абс = В – Р_вак (1.4)

При переводе давления, измеренного высотой ртутного столба, в другие единицы измерения давления вводится поправка на температуру:

В_о = В (1 - 0,0001721), (1.5)

где В_о - показания барометра, приведённые к 0° С,

В - действительная высота ртутного столба при температуре воздуха t°С,

0,000172 - коэффициент объёмного расширения ртути.

3. Третьей основной величиной, характеризующей состояние тела, является температура, которая выражается в зависимости от начала отчёта в градусах Кельвина (К) или в градусах Цельсия(ºС). В качестве единственной воспроизводимой опытом путём постоянной точки термодинамической температурной шкалы взята тройная точка воды, которой присвоены значения температуры 273,16 К (0,01°С), соответствующей температуре таянья льда. Тройная точка воды - это температура, при которой все три фазы (твёрдая, жидкая и газообразная) находятся в равновесии. Нижним пределом шкалы является абсолютный нуль. При этом температура кипения воды при нормальном атмосферном давлении соответствует 100°С. Температуру по международной практической температурной шкале, считываемую от 0° С, обозначают через t, а температуру по абсолютной шкале, отсчитываемую от температуры абсолютного нуля, обозначают Т и называют абсолютной температурой. Зависимость между ними имеет вид:

ТК = t°С + 273,15 (1.6)

В США и Англии для измерения температуры применяется шкала Фаренгейта (°F), по которой температура таянья льда и температура кипения воды соответственно равны 32°С и 212°С. Для перевода показания шкалы Фаренгейта в градусы Цельсияи обратно справедливы соотношения:

t°С = 5/9 (t°F - 32) (1.7)

t°F = 9/5 (t°С + 32) (1.8)

Пример:

Определить абсолютное давление пара в котле, если манометр показывает давление Р_ман= 1,3 бар, а атмосферное давление по ртутному барометру составляет Р_бар =735 мм рт.ст. при температуре t =24 °С

Решение:

Абсолютное давление определяется по уравнению (1.3):

Р_абс = Р_ман + В_о

где В_о - показания барометра, приведённые к 0° С, определяемые по формуле (1.5):

В_о = В (1 - 0,000172 t),

где В - атмосферное давление, следовательно:

В_о = 735 (1 - 0,000172·24)=731,96 мм рт. ст.= 731,96 ·1,33322·10^-3=0,976 бар, Р_абс = 1,3 + 0,976 = 2,276 бар

Ответ: абсолютное давление пара в котле равняется 2,276 бар

 

Практические задания

Задание № 1 Определить удельный объём и плотность газа при определённых условиях (при заданных массе и объеме)

 

Вариант
CН4	С2Ha	N2	O2	CO2	CO	C3H8	C4H10	SO2	SO3
m	кг	0,7	0,9	1,5	2,1	0,8	2,2	0,75	1,4	1,5	0,95
v	м2	1,2	1,35			2,5	1,8	2,1	2,5	1,23	0,58

 

Задание № 2 Задано давление воздуха по ртутному барометру. Выразить это давление в барах, Паскалях, МПа, кгс/см², м вод. с.

Вариант
Велич.	Ед. изм.
Р	мм рт. ст.

 

Задание № 3 Задана температура пара, выходящего из пароперегревателя, в °F. Перевести эту температуру в °С

Вариант
t	0F

 

Контрольные вопросы

1. Какому физическому явлению соответствует 0°С?

2. Какой температуре в °С соответствует 0°F?

3. Какими приборами измеряется атмосферное давление?

4. Перевести 39 кПа в м вод. ст.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

Тема: Основные термодинамические процессы

Цель работы: Формирование уменийпо расчёту параметров процессов Формируемые компетенции: ОК2, ОК4, ОК5

Ресурсы:

1. Барихина Н.В. Методические указания по выполнению заданий на практических занятиях [Текст]: - Екатеринбург: УПЭТ, 2013.-55с.

2. Бахшиева Л.Т., Кондрауров Б.П. [и др.] Техническая термодинамика и теплотехника: учебное пособие для вузов [Текст]: - М.: Изд. центр "Академия", 2008.-345с.

3. Прибытков И.А. Теоретические основы теплотехники: учеб. для студентов учреждений среднего профессионального образования[Текст]: – М.: Изд. центр "Академия", 2004.-276с.

Задание:

· ознакомиться с общими сведениями;

· выполнить задания №1÷6;

· ответить на контрольные вопросы.

Общие сведения:

· Основными термодинамическими процессами являются:

1. изохорный процесс - процесс сообщения или отвода тепла при постоянном объеме газа (V =const);

2. изобарный процесс - процесс сообщения или отвода тепла при постоянном давлении (р = const);

3. изотермический процесс - процесс сообщения или отвода тепла при постоянной температуре (t = const);

4. адиабатный процесс -процесс без сообщения или отвода тепла извне (q = 0);

5. политропный процесс - процесс, в котором изменение параметров подчиняется уравнению pvⁿ = const,

где n - величина, постоянная для данного процесса.

 

Изохорный процесс

В диаграмме Рv процесс изображается прямой 1-2, параллельной оси ординат. Уравнение прямой 1-2 (рисунок 2.1), называемой изохорой, v = const.

 

Рисунок 2.1 - PV и TS диаграммы изохорного процесса

Зависимость между начальными и конечными параметрами процесса:

(2.1)

Изменение внутренней энергии в Дж/кг:

Δ u = C_vm (t₂ - t_l) (2.2)

Если в процессе участвует М (кг) или V_н (м³), то количество тепла или изменение внутренней энергии газа подсчитывается по формуле:

Q_v = ΔU_v = MС_vm (t₂ – t₁) = V_нС¹_vm (t₂ - t₁) (25.3)

где V_н — количество газа в м³ при нормальных условиях.

В изохорном процессе газ работы не совершает (L =0)

 

Задание № 1. В закрытом сосуде заключен газ при разряжении Р_вак1и температуре t₁. Показание барометра - 760 мм рт. ст. До какой температуры нужно охладить газ, чтобы разряжение стало равным Р_вак2

Вариант
Рвак1	мм рт.ст.
tl	°С
Рвак2	мм рт.ст.								ПО

Изобарный процесс

В диаграмме Рv этот процесс изображается прямой 1-2, параллельной оси абсцесс. Уравнение прямой 1-2 (рисунок 2.2), называется изобарой, р = const.

Рисунок 2.2 - PV и TS диаграммы изобарного процесса

Зависимость между начальными и конечными параметрами процесса:

(2.4)

Работа 1 кг газа:

l=p(v₂-v₁) (2.5)

или l=R(T₂-T₁) (2.6)

Для газа массой М кг:

L = MР (v₂-v₁) = Р(V₂-V₁) (2.7)

или L = MR(t₂-t₁) (2.8)

Если в процессе р = const участвует М (кг) или V_н (м³), то количество тепла подсчитывается по формуле:

Q_р = MС_рm (t₂ – t₁) = V_нС¹_рm (t₂ - t₁) (2.10)

где V_н — количество газа в м³ при нормальных условиях.

Изменение внутренней энергии газа определяется по формуле:

Δu = C_vm(t₂ – t₁) (2.11)

или Δu =C_vm2 t₂ – C_vm1 t₁ (2.12)

Задание № 2. В цилиндре находится воздух при давлении Р и температуре t_l. От воздуха отводится тепло при постоянном давлении таким образом, что в конце процесса устанавливается температура t₂. Объем цилиндра, в котором находится воздух, V. Определить количество отведенного тепла, конечный объем, изменение внутренней энергии и совершенную работу сжатия. Зависимость теплоемкости от температуры считать нелинейной.

Вариант
Р	бар
tl	°С
t2	°С
V	л

Изотермический процесс

Кривая изотермического процесса, называется изотермой, в диаграмме Pv изображается равнобокой гиперболой (рисунок 5.3). Уравнение изотермы в

координатах PV: PV = const

Рисунок 2.3 - PV и TS диаграммы изотермического процесса

Зависимость между начальными и конечными параметрами определяется по формулам:

(2.13)

(2.14)

Работа 1 кг идеального газа определяется из уравнений:

l=RT In (2.15)

l=RT In (2.16)

l=P₁v₁ In (2.17)

l= P₁v₁ In (5.18)

Если в процессе участвует газ массой М кг, то полученные из формул (2.15) ÷(2.18) значения нужно увеличить в М раз. Можно также для этого случая в формулах (2.17)и(2.18) заменить удельный объем v полным объемом V. Получим:

L = Р₁V₁In (2.19)

L = Р₁V₁In (2.20)

Т. к. в изотермическом процессе t = const, то для идеального газа:

Δu = C_vm (t₂-t₁) = 0

Количество тепла, сообщаемого газу или отнимаемого от него, равно:

q_t=l (2.21)

или для газа массой М кг: Q_t = L (2.22)

Натуральный логарифм, входящий в формулы, может быть заменен десятичным по соотношению InN = 2,303IgN.

Значение работы изотермического сжатия для 1 кг различных газов при одинаковых условиях выражаются следующими уравнениями:

l₁ =R₁T In (2.23)

l₂ = R₂T In (2.24)

l₃ = R₃T In и т.д. (2.25)

следовательно l₁: l₂: l₃ = R₁: R₂: R₃, (2.26)

т.е работа изотермического сжатия пропорциональна газовой постоянной.

Задание № 3. 1кг воздуха при температуре t_l и начальном давлении Р₁ сжимается изотермически до конечного давления Р₂. Определить конечный объем, затрачиваемую работу и количество тепла, отводимого от газа.

Вариант
tl	ºС
Р1	бар
Р2	бар

Адиабатный процесс

Уравнение адиабаты в системе координат Рv (рисунок 2.4) при постоянной теплоемкости (Cv = const) для идеального газа pv^к = const,

где к - показатель адиабаты, к=С_р /С_v

 

Рисунок 2.4 - PV и TS диаграммы адиабатного процесса

Зависимость между начальными и конечными параметрами процесса:

- между Р и v:

(2.27)

- между Т и v:

(2.28)

- между Т и Р:

(2.29)

Работа 1 кг газа определяется по следующим формулам:

1= (P₁ v₁-Р₂v₂) (2.30)

1= [1- ] (2.31)

1= (Т₁ -Т₂) (2.32)

1= [1 - 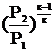] (2.33)

Для определения работы газа массой М кг нужно в формулах (2.30), (2.31) и (2.33) заметить удельный объем v общим объемом газа:

L = (P₁ V₁-Р₂V₂) (2.34)

L = 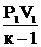[1- ] (2.35)

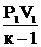L = [1 - 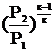] (2.36)

Формула (2.32) для газа массой M кг примет следующий вид:

L= (Т₁ -Т₂) (2.37)

Уравнение первого закона для адиабатного процесса имеет следующий

вид: Δu= - l (2.38)

т.е. изменение внутренней энергии газа и работа адиабатного процесса равна по величине и противоположна по закону.

Изменение внутренней энергии идеального газа а адиабатном процессе может быть также выражено уравнением:

Δu = C_vm (t₂ –t₁) (2.39)

Задание № 4. В баллоне емкостью V находится воздух при давлении Р₁ и температуре t_l. Давление окружающей среды Р₂. Определить работу, которая может быть произведена содержащимся в баллоне воздухом при расширении его до давления окружающей среды по изотерме и по адиабате. Определить также минимальную температуру, которую будет иметь воздух в баллоне, если открыть вентиль и выпускать воздух из баллона до тех пор, пока давление в нем не станет равным давлению окружающей среды и при условии, что теплообмен воздуха с окружающей средой будет отсутствовать.

Вариант
V	м3
P1	бар
t1	°C
P2	бар	0,5	0,8	0,9		1,2	1,3	1,5	1,7	1,9

 

Задание № 5. В газовом двигателе смесь газа и воздуха адиабатно сжимается так, что к концу сжатия ее температура оказывается на 200°С ниже температуры воспламенения газа. В начале сжатия давление Р₁ и температура t_l. Показатель адиабаты к=1,36; R=314 Дж/(кг К), температура воспламенения t _всп.

Определить величину работы сжатия и степень сжатия.

Вариант
P1	МПа	0,07	0,08	0,09	0,1	0,2	0,3	0,4	0,5	0,6	0,7
tl	°С
tвcn	°С

Политропный процесс

Уравнение политропы в системе координат Рv (рисунок 2.5) при постоянной теплоёмкости Рvⁿ =const,

где n — показатель политропы.

Рисунок 2.5 - PV диаграмма политропного процесса

Характеристикой политропного процесса является величина

φ = (2.40)

где к показатель адиабаты, к =

Рисунок 2.6 - PV диаграмма политропных процессов

По рисунку 2.6 можно по величине показателя политропы определить ее относительное расположение в диаграмме Рv, а также выяснить характер процесса, т.е. имеет ли место подвод или отвод тепла и увеличение или уменьшение внутренней энергии газа.

- Для процессов расширения:

1. n < 1 - тепло подводится (q>0), внутренняя энергия газа увеличивается (Δu>0);

2. к > n >1 - тепло подводится (q>0), внутренняя энергия газа уменьшается

(Δu <0);

3. n > к - тепло отводится (q<0), внутренняя энергия газа уменьшается

(Δu <0).

- Для процессов сжатия:

1. n < 1 - тепло отводится, внутренняя энергия газа уменьшается;

2. к> n >1 - тепло отводится, внутренняя энергия газа увеличивается;

3. n >к — тепло подводится, внутренняя энергия газа увеличивается.

Зависимость между начальными и конечными параметрами процесса:

- между Р и v:

(2.41)

- между Т и v:

(2.42)

- между Р и Т:

(2.43)

Работа 1 кг газа определяется по следующим формулам:

1= (P₁ v₁-Р₂v₂) (2.44)

1= [1- ] (2.45)

1= (Т₁ -Т₂) (2.46)

1= [1 - ] (2.47)

Если количество тепла, участвующего в процессе, известно, что работа может быть также вычислена по формуле:

1= q (2.48)

Для определения работы газа массой М кг нужно в формулах (2.44), (2.45) и (2.47) заметить удельный объем v общим объемом газа:

L = (P₁ V₁-Р₂V₂) (2.49)

L = [1- ] (2.50)

L = [1 - ] (2.51)

 

Формула (2.46) для газа массой M кг примет следующий вид:

L= (Т₁ -Т₂) (2.52)

или L = Q (2.53)

Теплоемкость политропного процесса определяется из уравнения:

с = (2.54).

или с=с_v (2.57).

Количество тепла, сообщаемого газу или отводимого от него:

q = c(t₂-t_l) = с_v (t₂ - t_l) (2.58)

Q = Mc(t₂-t_l) = M с_v (t₂ - t_l) (2.59)

Величина Q может быть также определена, если известна работа политропного процесса:

Q = L (2.60)

Изменение внутренней энергии газа в политропном процессе находится по формуле:

Δu = C_vm(t₂-t_l) (2.61)

Показатель политропного процесса определяется из уравнения:

n= (2.62)

Задание № 6. 1 кг воздуха при давлении P₁ и температуре t_l расширяется политропно до давления P₂. Определить конечное состояние воздуха, изменение внутренней энергии, количество подведенного тепла и полученную работу, если показатель политропы n =1,2.

Вариант
Рl	бар		2,6		3,5		4,4		5,5		6,3
tl	°С
Р2	бар	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0

 

 

Пример:

В закрытом сосуде емкостью V = 0,6 м³ содер­жится воздух при давлении Р₁ = 5 бари температуре t₁ = 20°С. В результате охлаждения сосуда воздух, содержащийся в нем, теряет тепло в количестве Q= -105 кДж. Принимая теплоемкость воздуха постоянной, опре­делить, какое давление и какая температура установятся после этого в сосуде.

Решение:

Из уравнения состояния Клапейрона-Менделеева масса воздуха в сосуде определяется по формуле:

М=

М= =3,57 кг

Количество тепла, отводимого от воздуха в процессе, определяется по уравнению:

Q= Mc_vm(t₂— t₁),

откуда t₂ = + t₁

где c_vm –средняя массовая изохорная теплоёмкость воздуха, определяемая по формуле:

c_vm=

где μc_vm –средняя мольная изохорная теплоёмкость воздуха, для двухатомных газов μc_vm=20,93;

μ – моль, для воздуха μ=28,96; следовательно:

c_vm=20,93/28,96=0,723 кДж/кг·К

t₂= +20=-20,7 °С

Из соотношения параметров в изохорном процессе:

давление в конечном состоянии определяется из уравнения:

Р₂=Р₁

Р₂=5· =4,3 бар

Ответ: после охлаждения сосуда в нём установится давление 4,3 бар, температура-20,7 ° С.

Контрольные вопросы

1. Какой закон применим для изотермического процесса?

2. Какой закон применим для изобарного процесса?

3. Какой закон применим для изохорного процесса?

4. Напишите формулу для определения показателя адиабаты в зависимости от теплоёмкости.

 

 

ПРАКТИЧЕСКОЕ ЗАДАНИЕ

Тема: Нахождение параметров водяного пара по hS диаграмме

Цель работы: Формирование уменийиспользования hS диаграммы и применения полученных знаний при решении задач

Формируемые компетенции: ОК2, ОК4, ОК5

Ресурсы:

1. Барихина Н.В. Методические указания по выполнению заданий на практических занятиях [Текст]: - Екатеринбург: УПЭТ, 2013.-55с.

2. Бахшиева Л.Т., Кондрауров Б.П. [и др.] Техническая термодинамика и теплотехника: учебное пособие для вузов [Текст]: - М.: Изд. центр "Академия", 2008.-345с.

3. Ривкин С.Л., Александров А.А. Термодинамические свойства воды и водяного пара [Текст]: - М.: Энергоатомиздат, 2004.-456с.

Задание:

· ознакомиться с общими сведениями;

· выполнить задания №1, 2 и 3;

· ответить на контрольные вопросы.

Общие сведения:

· Наряду с таблицами насыщенного пара исключительно важное значение в теплотехнических расчётах имеют диаграммы Ts и hs. На рисунке 4.1 изображена диаграмма Ts для водяного пара. Кривая О₁K — нижн