Все выводы и определения, относящиеся к линейной дискретной системе, справедливы для цифрового фильтра.
Рассмотрим классификацию цифровых фильтров.
По диапазону частот сигналов, пропускаемых на
выход, фильтры подразделяются на
· фильтры нижних частот (ФНЧ),
· фильтры верхних частот (ФВЧ),
· полосовые фильтры (ПФ),
· режекторные фильтры (РФ).
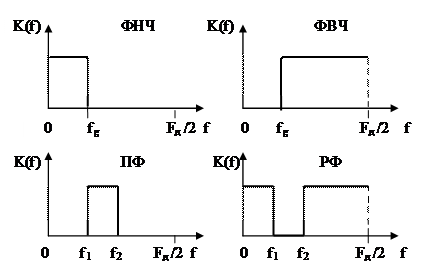
Рисунок 1. АЧХ четырёх типов цифровых фильтров
Из рисунка видно, что у ФНЧ полоса пропускания находится в интервале от нуля до граничной частоты fg, а частота задерживания в интервале от fg до Fд /2.
У ФВЧ полоса пропускания в интервале от граничной частоты fg до Fд /2, а полоса задерживания в интервале от нуля до fg.
Полосовой фильтр имеет одну полосу пропускания от f1 до f2 и две полосы задерживания: левая полоса задерживания от нуля до f1, правая полоса задерживания от f2 до Fд /2.
Режекторный фильтр имеет одну полосу задерживания от f1 до f2 и две полосы пропускания: левую от нуля до f1 и правую от f2 до Fд /2.
У реальных цифровых фильтров, как и у аналоговых, существует переходная полоса между полосой пропускания и полосой задерживания.
По характеру зависимости текущего отсчёта выходного сигнала yn от отсчётов входного и выходного сигналов цифровые фильтры подразделяются на
· нерекурсивные фильтры и
· рекурсивные фильтры.
Определения рекурсивных и нерекурсивных фильтров соответствуют определениям рекурсивных и нерекурсивных линейных дискретных систем, которые даны в разделе 2.5.
По виду импульсной характеристики
КИХ - фильтры (фильтры с конечной импульсной характеристикой) и
БИХ – фильтры (фильтры с бесконечной импульсной характеристикой).
Рассмотрим формы программной реализации цифровых фильтров.
|
|
1.Прямая форма.
Прямая форма программной реализации цифрового фильтра – это программирование разностного уравнения линейной дискретной системы
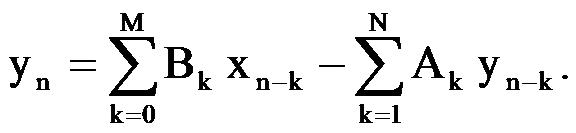
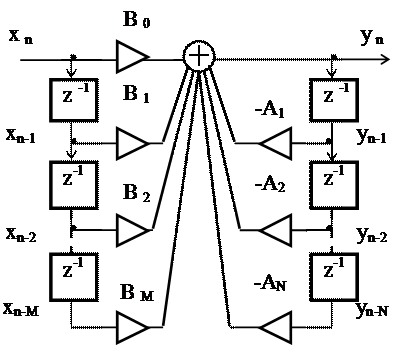
Рисунок 2– Прямая форма программной реализации
фильтра
В разделе 2.5 было показано, что разностному уравнению линейной дискретной системы соответствует системная функция
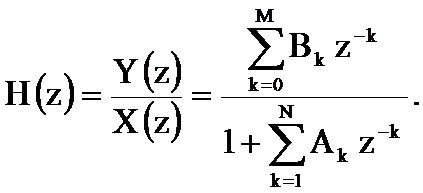
В фильтре рисунка 2 текущий отсчет выходного сигнала yn зависит как от отсчётов входного сигнала 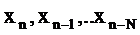 , так и отсчётов выходного сигнала
, так и отсчётов выходного сигнала 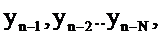 следовательно, этот фильтр является рекурсивным. При равенстве нулю всех коэффициентов
следовательно, этот фильтр является рекурсивным. При равенстве нулю всех коэффициентов 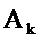 он становится нерекурсивным.
он становится нерекурсивным.
2. Каноническая форма
Представим системную функцию H(z) в виде произведения двух функций
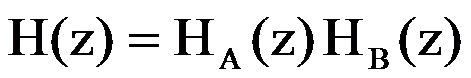 ,
,
где 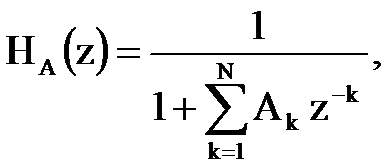
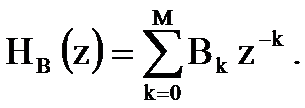
Согласно последнему соотношению цифровой фильтр с системной функцией H(z) можно представить в виде последовательного соединения двух фильтров с системными функциями HA(z) и HB(z)
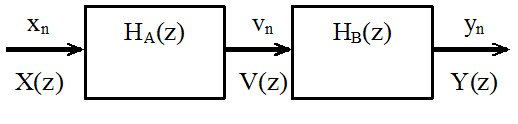
Рисунок 3 – Представление фильтра с прямой формой реализациив виде последовательного соединения двух фильтров
Действительно,
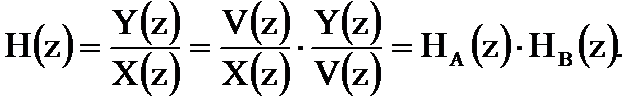
После детализации укрупнённых блоков рисунка 3 получим схему, представленную на рисунке 4
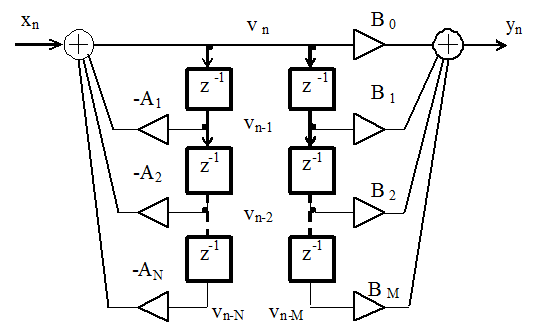
Рисунок 4 – Детальный алгоритм представления фильтра с прямой реализацией в виде последовательного соединения двух фильтров
Каждому элементу задержки на схеме фильтра соответствует ячейка памяти цифрового устройств. Из рисунка видно, что для хранения одной переменной используется две ячейки памяти. Такое дублирование устраняется использованием одной линией задержки максимальной длины. При этом схема фильтра при M=N преобразуется к виду, представленному на рисунке 5. Это и есть каноническая форма программной реализации фильтра.
|
|
Достоинством канонической формы является меньшее количество элементов задержки, следовательно, ячеек памяти вычислительного устройства.
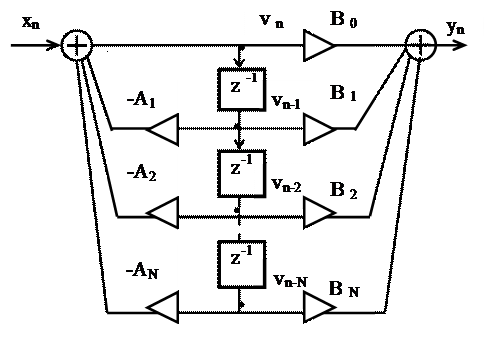
Рисунок 5– Каноническая форма
программной реализации фильтра
Однако обычно вместо структуры, изображенной на рисунке 5, используется параллельное или последовательное соединение звеньев второго порядка. Такое представление фильтра связано с возможностью представления системной функции H(z) в виде произведения или суммы системных функций с полиномами второго порядка в числителе и знаменателе
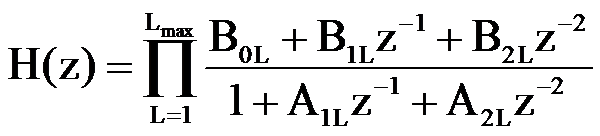 ,
,
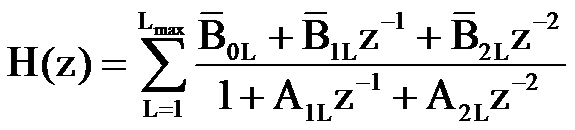 ,
,
где L – порядковый номер звена,
Lmax – максимальное значение номера звена
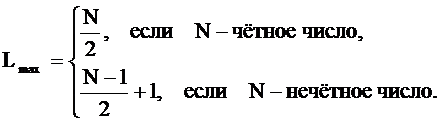
При четном N фильтр состоит из N/2 звеньев второго порядка, при нечетном N фильтр состоит из одного звена первого порядка и (N-1)/2 звеньев второго порядка.
Системная функция звена первого порядка отличается от системной функции звена второго порядка тем, что коэффициенты B2 и A2 равны нулю.
Выражению для H(z) в виде произведения соответствует схема рисунка 6 а, а выражению в виде суммы – схема рисунка 6 б.
Типовая схема звена второго порядка приведена на рисунке 7. В англоязычной литературе звено второго порядка принято называть биквадратным звеном. На входе звена показан масштабный коэффициент ML (как правило, меньше единицы), предотвращающий появление в процессе вычислений значений сигналов фильтра, выходящих за пределы разрядной сетки вычислительного устройства с фиксированной точкой.
|
|
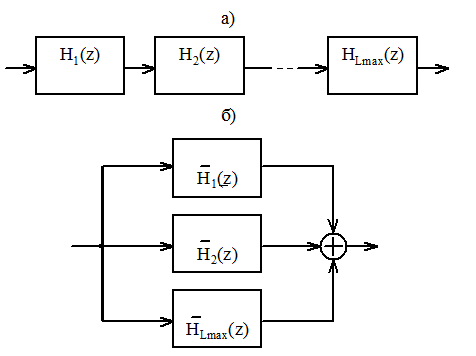
Рисунок 6- Последовательное (а) и параллельное
(б) соединение звеньев фильтра
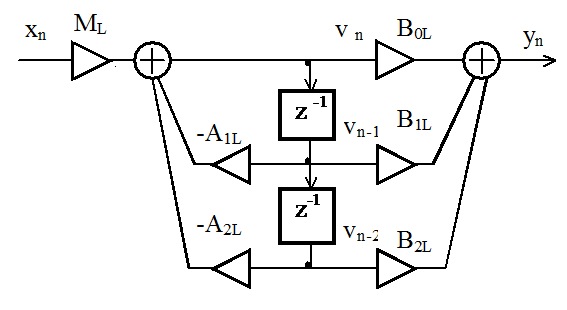
Рисунок 7 – Типовое звено второго порядка
2.9. Фильтры с конечной импульсной
характеристикой
2.9.1. Фильтр с линейной ФЧХ
Случай 1. Симметричная импульсная
характеристика, длина импульсной
характеристики N – нечётное число
.
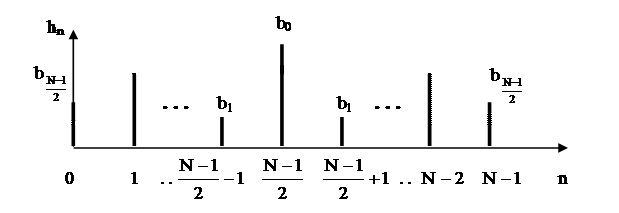
Рисунок 2.22. Симметричная импульсная характеристика КИХ – фильтра при нечётном N
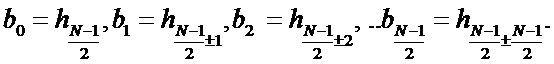
В общем случае
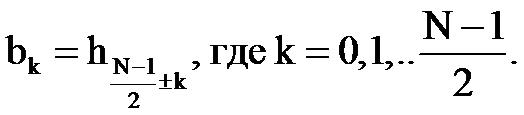
Определим системную функцию как прямое Z – преобразование импульсной характеристики
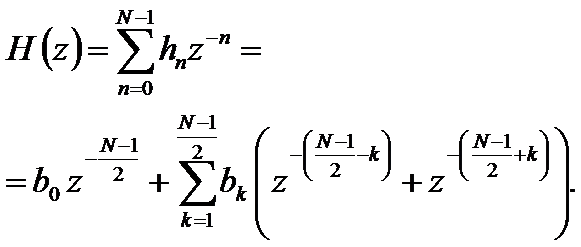
Найдём комплексный коэффициент передачи, используя подстановку 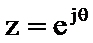 ,
,
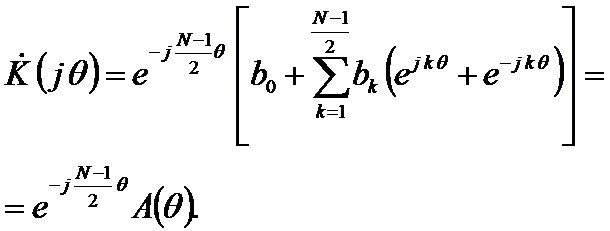
где 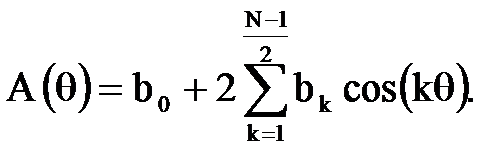
Тогда АЧХ 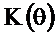 и ФЧХ
и ФЧХ 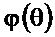 при нечётном N определятся следующими соотношениями:
при нечётном N определятся следующими соотношениями:
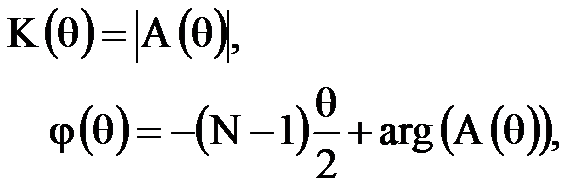
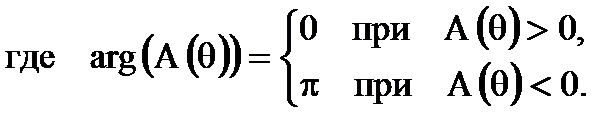
Из последнего соотношения видно, что ФЧХ фильтра линейная (линейно-ломаная), а АЧХ определяется абсолютной величиной суммы ряда косинусов.
На рисунке 2.23 приведена структурная схема фильтра с линейной ФЧХ при нечетном N=5.
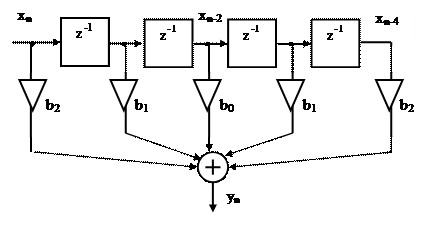
Рисунок 2.23. КИХ-фильтр с линейной ФЧХ при нечётном N=5
При длине импульсной характеристики, определяемой нечётным числом N, количество элементов задержки является чётным числом N-1, а коэффициенты системной функции симметричны относительно середины линии задержки.
Случай 2. Симметричная импульсная характеристика, длина импульсной характеристики N – чётное число
В этом случае ось симметрии проходит между центральными отсчетами с номерами 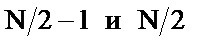 и
и 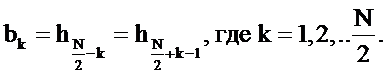 .
.
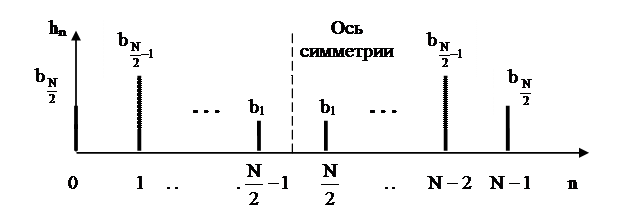
Симметричная импульсная характеристика КИХ – фильтра при чётном N
Определим системную функцию фильтра
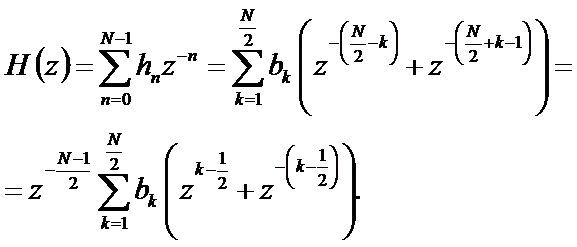
Подставив в выражение для системной функции 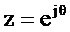 ,
,
найдём комплексный коэффициент передачи фильтра
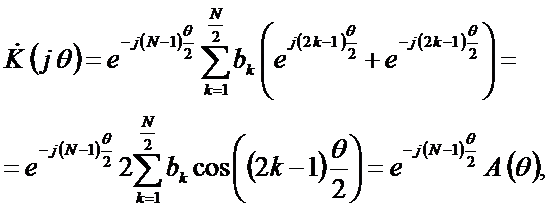 (2.23)
(2.23)
где 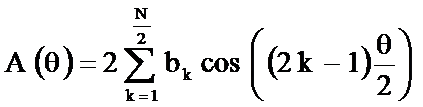
Тогда АЧХ 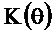 и ФЧХ
и ФЧХ 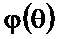 при чётном N определятся следующими соотношениями:
при чётном N определятся следующими соотношениями:
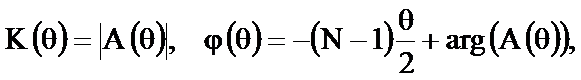
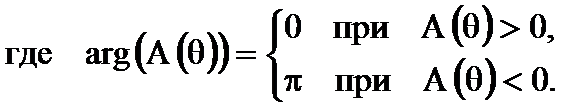
Из (2.24) видно, что ФЧХ линейна.
На рисунке 2.25 приведена структурная схема фильтра с линейной ФЧХ при четном N=4.
При длине импульсной характеристики, определяемой чётным числом N, количество элементов задержки является нечётным числом N-1, а коэффициенты системной функции симметричны относительно центрального элемента линии задержки.
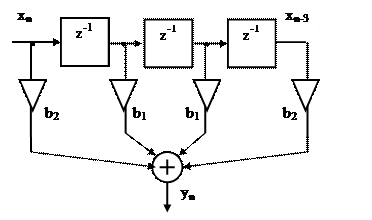
Рисунок 2.25. КИХ-фильтр с линейной ФЧХ при чётном N=4
2.9.2. Однородный фильтр
Однородным называется фильтр, у которого все отсчёты импульсной характеристики одинаковы. Для уменьшения количества операций умножения при реализации фильтра эти отсчёты принимаются равными единице, а коэффициент передачи фильтра регулируется масштабным коэффициентом на его входе. Однородный фильтр называют также фильтром скользящего среднего.
На рисунке 2.26 приведена импульсная характеристика однородного фильтра длиной N=5, а на рисунке 2.27 его структурная схема.
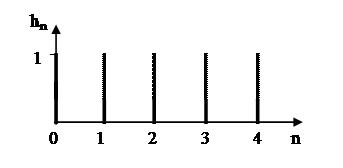
Рисунок 2.26. Импульсная характеристика однородного фильтра при N=5
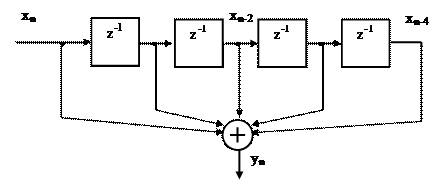
Рисунок 2.27. Однородный фильтр
Пусть требуется определить и построить графики АЧХ и ФЧХ фильтра. Решим эту задачу двумя способами.
Способ 1. Воспользуемся соотношениями (2.21) при N=5 и bk=1 для k=0, 1, 2.
Тогда
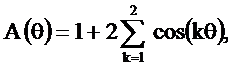
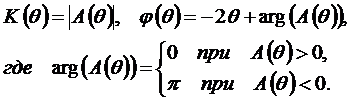 (2.25)
(2.25)
На рисунках 2.28 и 2.29 приведены АЧХ и ФЧХ однородного фильтра при N=5
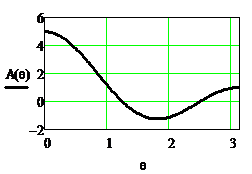
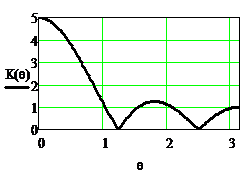
Рисунок 2.28. Функция 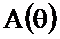 и АЧХ однородного фильтра
и АЧХ однородного фильтра 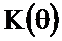
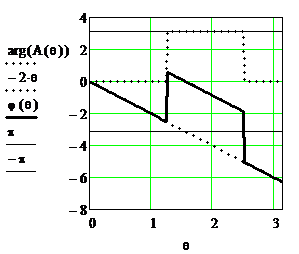
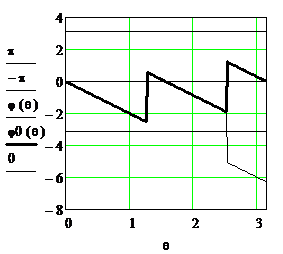
Рисунок 2.29. ФЧХ однородного фильтра до 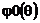 и после
и после 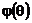 приведения в интервал от -
приведения в интервал от - 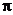 до
до 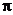
Из АЧХ следует, что однородный фильтр является фильтром нижних частот. Особенностью АЧХ являются пульсации в полосе задерживания. Максимальный коэффициент передачи фильтра равен K(0)=5. Чтобы его уменьшить, например, до единицы, нужно использовать на входе фильтра масштабный коэффициент M=1/5, как это показано на рисунке 2.30.
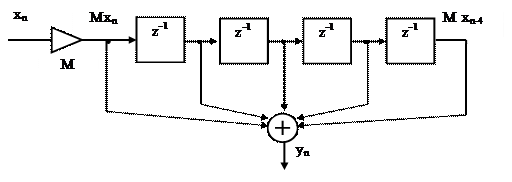
Рисунок 2.30. Однородный фильтр с масштабным коэффициентом M на входе
На рисунке 2.29 слева сплошными линиями представлена ФЧХ 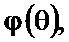 рассчитанная по (2.25), а пунктиром показаны её составляющие
рассчитанная по (2.25), а пунктиром показаны её составляющие 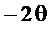 и
и 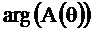 .
.
Однако общепринятым является представление ФЧХ в интервале от 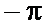 до
до 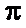 . Такое представление связано с периодичностью синусоидального сигнала. Ведь ФЧХ показывает, какой фазовый сдвиг приобретает синусоидальный сигнал при прохождении через фильтр, а для синусоиды фазовый сдвиг, кратный
. Такое представление связано с периодичностью синусоидального сигнала. Ведь ФЧХ показывает, какой фазовый сдвиг приобретает синусоидальный сигнал при прохождении через фильтр, а для синусоиды фазовый сдвиг, кратный 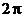 , эквивалентен нулевому фазовому сдвигу. Следовательно, ФЧХ
, эквивалентен нулевому фазовому сдвигу. Следовательно, ФЧХ 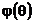 можно ввести в интервал от
можно ввести в интервал от 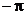 до
до 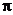 путем прибавления или вычитания целого числа
путем прибавления или вычитания целого числа 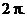
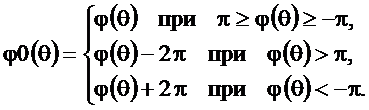 (2.26)
(2.26)
Если после выполнения (2.26) 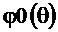 не войдёт в заданный интервал, то (2.26) нужно выполнить повторно, предварительно приняв
не войдёт в заданный интервал, то (2.26) нужно выполнить повторно, предварительно приняв 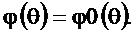
В рассматриваемом случае достаточно прибавить к 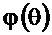
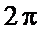 в интервале значений
в интервале значений 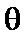 , при которых
, при которых 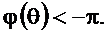 В результате получается ФЧХ
В результате получается ФЧХ 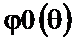 , приведённая на рисунке 2.29 справа. На этом же рисунке приведена исходная ФЧХ
, приведённая на рисунке 2.29 справа. На этом же рисунке приведена исходная ФЧХ 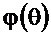 , которая отличается от
, которая отличается от 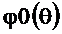 только на участке, где
только на участке, где 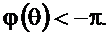 .
.
Способ 2. В соответствии со схемой 2.27 запишем
разностное уравнение
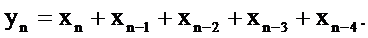
Найдём Z-преобразование последовательности 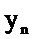
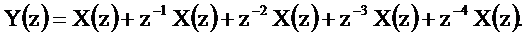
Определим системную функцию
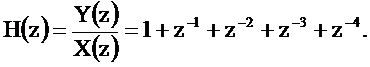
Используя подстановку 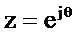 , получим выражение для комплексного коэффициента передачи
, получим выражение для комплексного коэффициента передачи
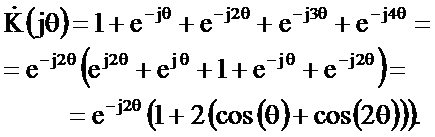
Из последнего соотношения получим
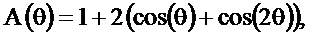
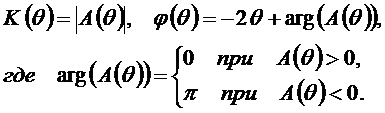
Как видно, полученные соотношения не отличаются от (2.25).
Выясним влияние длины импульсной характеристики N на АЧХ и ФЧХ фильтра. Для этого выполним расчёт АЧХ и ФЧХ при N=10. Из (2.24) при 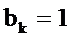 получим
получим
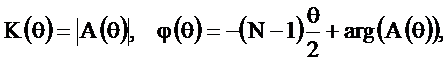
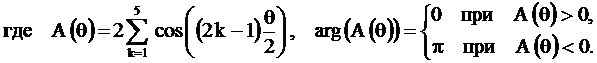
Рассчитанные по этим формулам функция 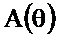 и АЧХ
и АЧХ 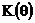 приведены на рисунке 2.30.
приведены на рисунке 2.30.
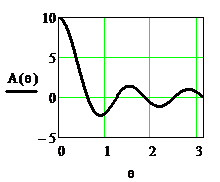
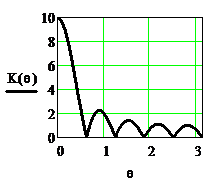
Рисунок 2.30. Функция 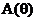 и АЧХ однородного фильтра при N=10
и АЧХ однородного фильтра при N=10
На рисунке 2.31 представлены ФЧХ 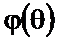 до приведения в стандартный интервал от –π до π, ФЧХ
до приведения в стандартный интервал от –π до π, ФЧХ 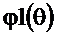 , равная
, равная 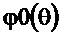 после первого применения соотношения (2.26), и ФЧХ
после первого применения соотношения (2.26), и ФЧХ 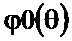 в стандартном интервале после второго применения (2.26).
в стандартном интервале после второго применения (2.26).
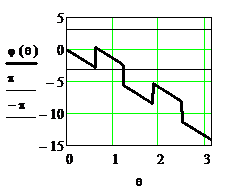
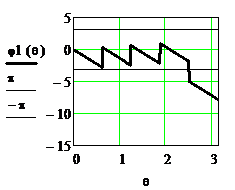
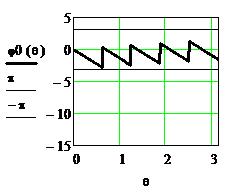
Рисунок 2.31. ФЧХ однородного фильтра при N=10 без приведения и с последовательным приведением в интервал от 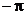 до
до 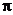
На рисунке 2.32 приведены АЧХ однородных фильтров с масштабными коэффициентами на входе, выбранных из условия получения максимального коэффициента передачи фильтров, равного единице, при N=5 и N=10.
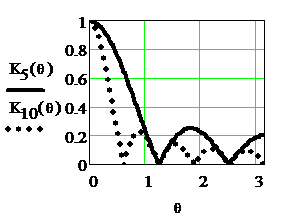
Рисунок 2.32. АЧХ однородных фильтров при N=5 (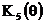 ) и N=10 (
) и N=10 (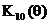
Из рисунка видно, что увеличение длины линии задержки
· сужает полосу пропускания фильтра,
· увеличивает частоту пульсаций АЧХ в полосе задерживания,
· уменьшает амплитуду пульсаций в полосе задерживания.
2.9.3. Триангулярный фильтр
Триангулярным называется фильтр с треугольной
огибающей отсчетов импульсной характеристики
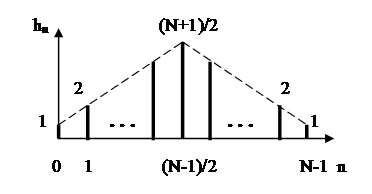
Рисунок 2.33. Импульсная характеристика триангулярного фильтра
При N=3 и минимальном значении отсчёта, равным
единице, максимальный отсчёт с номером 1 равен 2,
при N=5 максимальный отсчёт равен 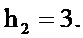
Поскольку импульсная характеристика симметрична относительно её центрального отсчёта, то триангулярный фильтр является фильтром с линейной ФЧХ.
На рисунке показана импульсная характеристика с минимальным значением отсчёта, равным единице. В общем случае все отсчеты этой характеристики могут быть пропорционально уменьшены или увеличены.
Треугольная импульсная характеристика триангулярного фильтра hn может быть получена как дискретная свёртка двух одинаковых импульсных характеристик h0n однородного фильтра
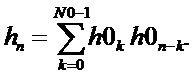
Процесс получения отсчётов импульсной характеристики триангулярного фильтра иллюстрирует рисунок 2.32.
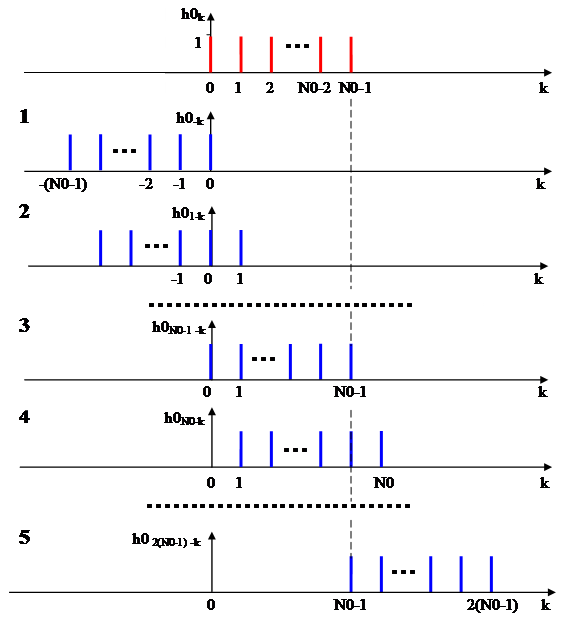
Рисунок 2.34. Дискретная свёртка импульсных характеристик двух одинаковых однородных фильтров
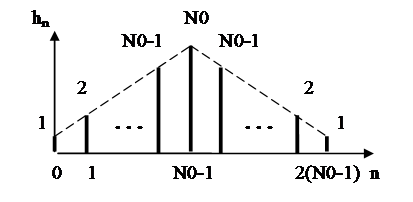
Временная диаграмма дискретной свёртки импульсных характеристик двух одинаковых однородных фильтров
Сравнение рисунков 33 2.35 и 2. показывает, что временная диаграмма дискретной свёртки не отличается от импульсной характеристики триангулярного фильтра, если выполняется условие
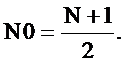
Определим системную функцию триангулярного фильтра 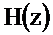 , воспользовавшись соотношением для дискретной свёртки (2.26) и учитывая, что прямое Z-преобразование дискретной свёртки равно произведению Z-преобразований свёртываемых последовательностей,
, воспользовавшись соотношением для дискретной свёртки (2.26) и учитывая, что прямое Z-преобразование дискретной свёртки равно произведению Z-преобразований свёртываемых последовательностей,
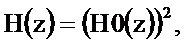
где 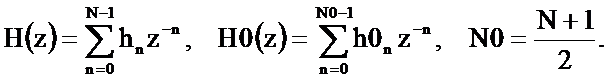
Из последнего соотношения следует связь между комплексными коэффициентами передачи триангулярного и однородного фильтров
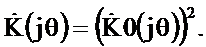 (2.28)
(2.28)
Если 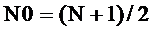 является нечётным числом, то подставляя (2.21) в последнее соотношение при bk=1 и длине импульсной характеристики однородного фильтра N0, получим
является нечётным числом, то подставляя (2.21) в последнее соотношение при bk=1 и длине импульсной характеристики однородного фильтра N0, получим
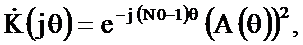
где 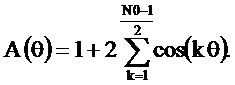
Из последнего соотношения найдём АЧХ 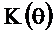 и ФЧХ
и ФЧХ 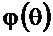 без приведения в интервал от
без приведения в интервал от 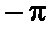 до
до 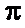
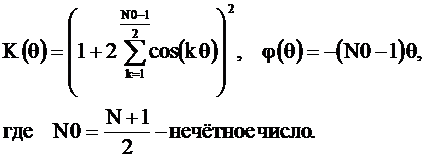 (2.29)
(2.29)
Если  является чётным числом, то подставляя (2.23) в последнее соотношение при bk=1 и длине импульсной характеристики однородного фильтра N0, получим
является чётным числом, то подставляя (2.23) в последнее соотношение при bk=1 и длине импульсной характеристики однородного фильтра N0, получим

где 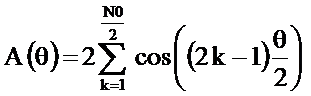 .
.
Из последнего соотношения найдём АЧХ 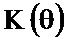 и ФЧХ
и ФЧХ 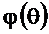 без приведения в интервал от
без приведения в интервал от 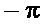 до
до 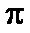
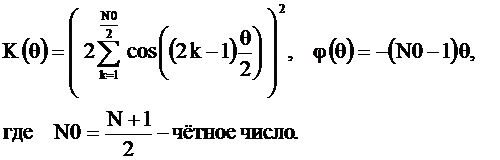 (2.30)
(2.30)
Выполним расчёт АЧХ и ФЧХ триангулярного фильтра рисунка 2.36
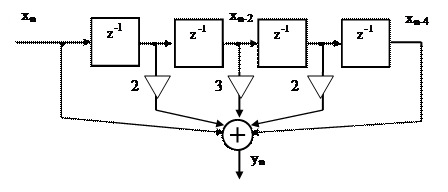
Рисунок 2.36. Триангулярный фильтр при N=5
Определим длину импульсной характеристики соответствующего однородного фильтра
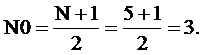
Поскольку N0=3 является нечётным числом расчет АЧХ и ФЧХ выполним по (2.29)
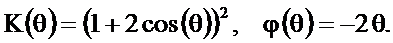
На рисунке 2.37 приведены АЧХ 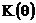 фильтра, ФЧХ
фильтра, ФЧХ 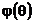 рассчитанная по последней формуле, и ФЧХ
рассчитанная по последней формуле, и ФЧХ 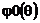 , приведённая в стандартный интервал
, приведённая в стандартный интервал
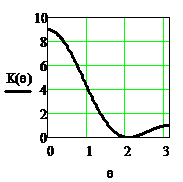
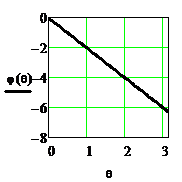
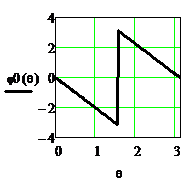
Рисунок 2.37. АЧХ и ФЧХ триангулярного фильтра при длине
импульсной характеристики N=5
Из рисунка видно, что триангулярый фильтр, как и однородный, является фильтром нижних частот.
На рисунке 2.38 приведены АЧХ триангулярного и однородного фильтров с N=5 и с одинаковыми значениями максимального коэффициента передачи за счёт соответствующего выбора масштабных коэффициентов (Mo=1/5, Mt=1/9
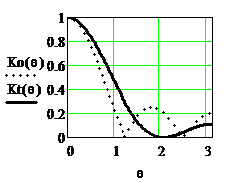
Рисунок 2.38. АЧХ триангулярного и однородного фильтров при N=5
Из рисунка видно, что АЧХ триангулярного фильтра имеет меньший уровень пульсаций в полосе задерживания по сравнению с АЧХ однородного фильтра, но большую ширину главного лепестка АЧХ.
2.9.4. Гребенчатый фильтр
На рисунке 2.39 приведена структурная схема гребенчатого фильтра, в состав которого входит линия задержки из N-1 элемента. Коэффициент b может принимать два значения b=1 или b= -1.
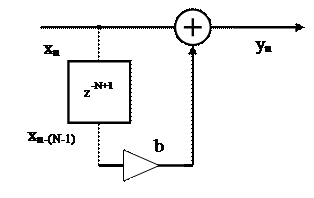
Рисунок 2.39
На рисунке 2.40 приведены две импульсные характеристики фильтра при b=1 и при b= -1.
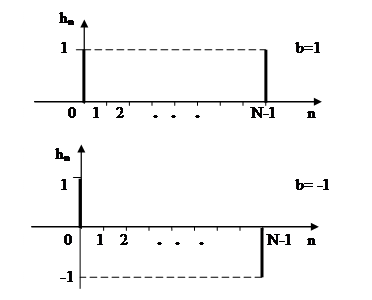
Рисунок 2.40. Импульсные характеристики гребенчатых фильтров
Определим системную функцию фильтра двумя способами:
Способ 1.
Системная функция является прямым Z-преобразованием импульсной характеристики
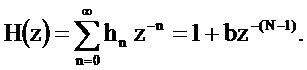
Способ 2.
Воспользовавшись схемой рисунка 2.39 запишем разностное уравнение
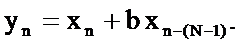
Выразим Z-преобразование выходного сигнала через Z-преобразование входного сигнала
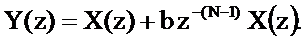
Определим системную функцию
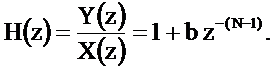
Комплексный коэффициент передачи фильтра равен
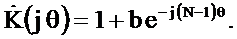
Определим комплексный коэффициент передачи фильтра при b=1
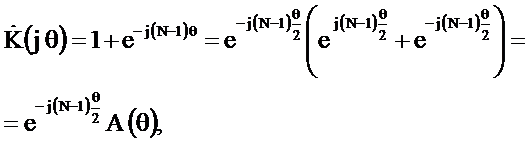
где 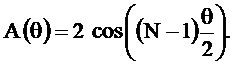
Найдём АЧХ и ФЧХ фильтра
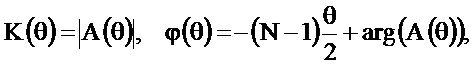
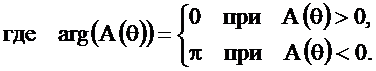
На рисунке 2.41 приведены функция 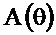 и АЧХ
и АЧХ 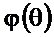 , а на рисунке 2.42 – ФЧХ
, а на рисунке 2.42 – ФЧХ 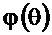 и ФЧХ
и ФЧХ 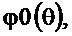 приведённая в стандартный интервал от
приведённая в стандартный интервал от 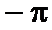 до
до 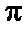 . ФЧХ
. ФЧХ 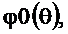 получена в результате двукратного использования соотношения (2.26).
получена в результате двукратного использования соотношения (2.26).
Рисунок 2.41. Функция 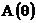 и АЧХ
и АЧХ 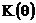 при b=1
при b=1
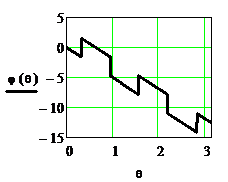
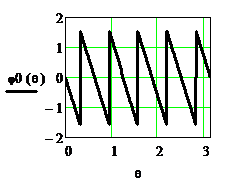
Рисунок 2.42. ФЧХ 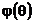 и ФЧХ
и ФЧХ 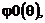 приведённая в стандартный интервал
приведённая в стандартный интервал
Определим комплексный коэффициент передачи фильтра при b=-1
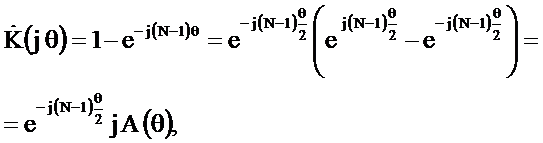
где 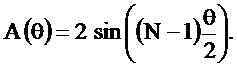
Найдём АЧХ и ФЧХ фильтра
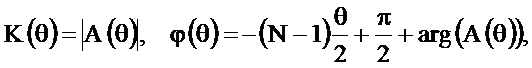
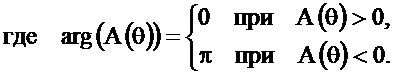
На рисунке 2.43 приведены функция 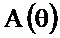 и АЧХ
и АЧХ 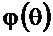 , а на рисунке 2.44 – ФЧХ
, а на рисунке 2.44 – ФЧХ 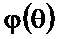 и ФЧХ
и ФЧХ 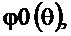 приведённая в стандартный интервал от
приведённая в стандартный интервал от 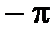 до
до 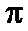 .
.
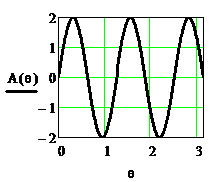
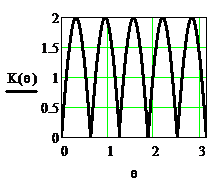
Рисунок 2.43. Функция 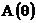 и АЧХ
и АЧХ 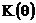 при b= -1
при b= -1
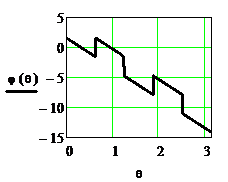
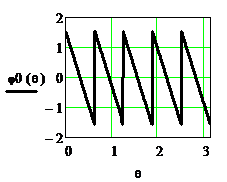
Рисунок 2.44. ФЧХ 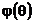 и ФЧХ
и ФЧХ 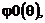 приведённая в стандартный интервал
приведённая в стандартный интервал
Из рисунков видно, что АЧХ фильтра состоит из одинаковых лепестков, количество и ширина которых зависят от длины импульсной характеристики. Диапазон нормированных круговых частот, соответствующий ширине лепестка, равен 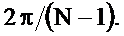 С увеличением длины импульсной характеристики N ширина лепестка уменьшается, а их количество увеличивается, и АЧХ становится похожей на гребёнку, поэтому фильтр называется гребенчатым.
С увеличением длины импульсной характеристики N ширина лепестка уменьшается, а их количество увеличивается, и АЧХ становится похожей на гребёнку, поэтому фильтр называется гребенчатым.
ФЧХ фильтра является линейно-ломаной, однако, в пределах каждого лепестка она линейна как при b=1, так и при b= -1.
2.10. Рекурсивные цифровые фильтры
2.10.1. Цифровой резонатор
Цифровой резонатор (рисунок 2.45) представляет собой звено второго порядка (рисунок 2.21), у которого коэффициенты системной функции B1 и B2 равны нулю, а коэффициент B0=1.
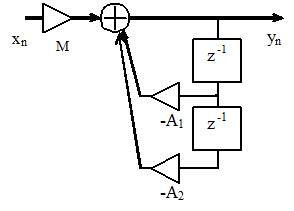
Рисунок 2.45. Цифровой резонатор
Для определения системной функции резонатора запишем разностное уравнение
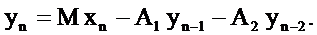
Перейдём от разностного уравнения к уравнению для Z-преобразований дискретных сигналов
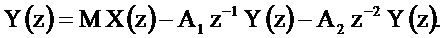
Из последнего уравнения выразим 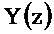 через
через 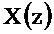
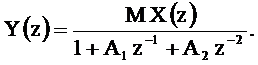
Определим системную функцию фильтра
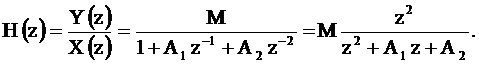 (2.31)
(2.31)
Определим полюсы системной функции. Для этого приравняем знаменатель нулю и найдем корни полученного квадратного уравнения

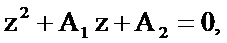
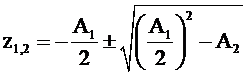 .
.
При этом системная функция преобразуется к виду
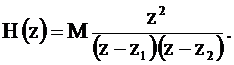 (2.32)
(2.32)
В цифровом резонаторе полюсы системной функции должны быть комплексно-сопряжёнными.
Следовательно, должно выполняться условие
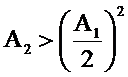 .
.
При этом условии полюсы системной функции определяются следующим соотношением
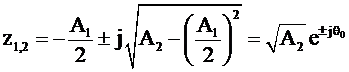 , (2.33)
, (2.33)
где  .
.
На рисунке 2.46 показаны полюсы системной функции резонатора на комплексной плоскости z. Окружность единичного радиуса с центром в начале координат является геометрическим местом точек, для которых выполняется условие
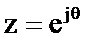 .
.
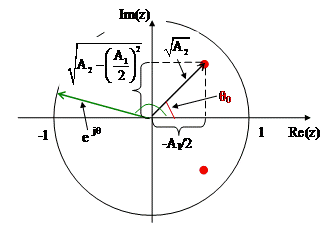
Рисунок 2.46. Полюсы системной функции z1 и z2
При изменении θ от 0 до π частота 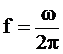 изменяется от 0 до FД / 2. При этом конец вектора
изменяется от 0 до FД / 2. При этом конец вектора 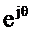 перемещается по окружности единичного радиуса. Расстояние конца этого вектора от полюса системной функции минимально при
перемещается по окружности единичного радиуса. Расстояние конца этого вектора от полюса системной функции минимально при 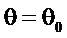 , т.е. при
, т.е. при 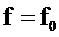 , где
, где 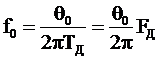 - резонансная частота резонатора.
- резонансная частота резонатора.
Подставляя в последнее соотношение θ0 из (2.33), получим
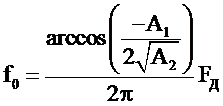 . (2.34)
. (2.34)
Из последнего соотношения видно, что резонансная частота прямо пропорциональна частоте дискретизации FД и зависит от коэффициентов системной функции A1 и A2. При A1=0 резонансная частота равна четверти частоты дискретизации, при A1<0 резонансная частота меньше четверти частоты дискретизации, а при A1> 0 – больше четверти частоты дискретизации.
Сначала рассмотрим частный случай настройки резонатора на частоту, равную четверти частоты дискретизации, при 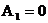 и определим комплексный коэффициент передачи, АЧХ и ФЧХ резонатора.
и определим комплексный коэффициент передачи, АЧХ и ФЧХ резонатора.
Подставляя в (2.31) 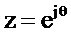 , получим
, получим
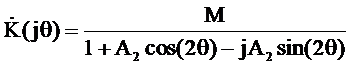 .
.
Последнее соотношение позволяет определить АЧХ и ФЧХ резонатора:
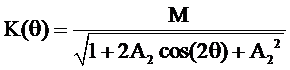 , (2.35)
, (2.35)
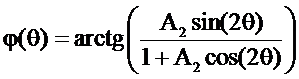 . (2.36)
. (2.36)
Из (2.35) видно, что на резонансной частота при 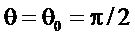 резонансный коэффициент передачи равен
резонансный коэффициент передачи равен
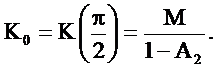 (2.37)
(2.37)
Из этого же соотношения следует, что
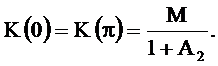
Например, при M=1, A2=0.999 резонансный коэффициент передачи равен 1000, а коэффициенты передачи на границах рабочего интервала примерно равны 0.5.
На рисунке 2.47 приведена АЧХ, рассчитанная по (2.35), а на рисунке 2.48 – ФЧХ, рассчитанная по (2.36) при A2=0.9, M=1-A2.
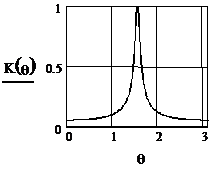
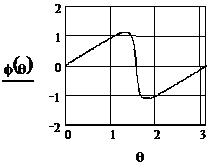
Рисунок 2.47 -АЧХ резонатора Рисунок 2.48 -ФЧХ резонатора
при 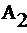 =0.9,
=0.9, 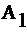 =0, M=1-
=0, M=1- 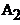 при
при 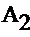 =0.9,
=0.9, 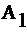 =0
=0
Из рисунка 2.47 видно, что АЧХ цифрового резонатора по форме похожа на резонансную кривую аналогового колебательного контура. ФЧХ резонатора (рисунок 2.48) не линейна, фазовые сдвиги, вносимые резонатором на частотах 0, 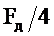 и
и 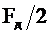 , равны нулю. Фазовый сдвиг на частота ниже частоты
, равны нулю. Фазовый сдвиг на частота ниже частоты 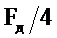 положительный, а на частотах выше
положительный, а на частотах выше 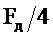 отрицательный. Вблизи резонансной частоты ФЧХ цифрового резонатора подобна ФЧХ аналогового колебательного контура, а при больших расстройках существенно отличается.
отрицательный. Вблизи резонансной частоты ФЧХ цифрового резонатора подобна ФЧХ аналогового колебательного контура, а при больших расстройках существенно отличается.
АЧХ и ФЧХ при A1=0, A2=0.99 приведены на рисунках 2.49 и 2.50 соответственно.
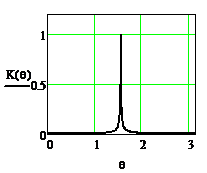
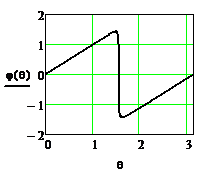
Рисунок 2.49 -АЧХ резонатора Рисунок 2.50 -ФЧХ резонатора
при 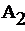 =0.99,
=0.99, 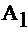 =0, M=1-
=0, M=1- 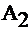 при
при 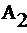 =0.99,
=0.99, 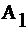 =0
=0
Сравнение характеристик при разных значениях коэффициента А2 показывает, что при стремлении А2 к единице резонанс становится более острым и увеличивается крутизна ФЧХ вблизи резонансной частоты.
А теперь выясним, как влияет коэффициент A1 на АЧХ и ФЧХ цифрового резонатора.
Для этого рассмотрим АЧХ и ФЧХ при А1<0 и при A1>0. Соответствующие графики приведены на рисунках 2.51.. 2.54.

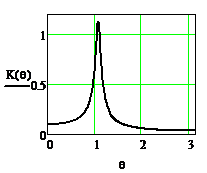
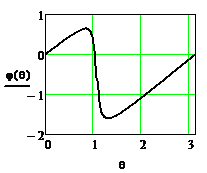
Рисунок 2.51 - АЧХ резонатора Рисунок 2.52 -ФЧХ резонатора при 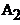 =0.9,
=0.9, 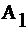 = -0.9, M=1-
= -0.9, M=1- 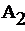 при
при 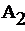 =0.9,
=0.9, 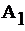 = -0.9
= -0.9
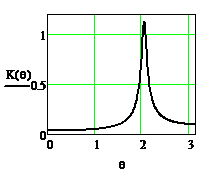
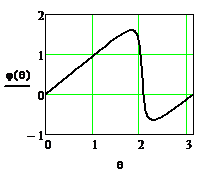
Рисунок 2.53 - AЧХ резонатора Рисунок 2.54 - ФЧХ резонатора
при 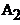 =0.9,
=0.9, 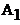 = 0.9, M=1-
= 0.9, M=1- 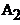 при
при 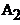 =0.9,
=0.9, 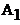 =0.9
=0.9
Из приведенных рисунков видно, что коэффициент А1 влияет на резонансную частоту резонатора. В результате АЧХ и ФЧХ сдвигаются вдоль оси частот. При этом нарушается симметрия АЧХ, становятся различными абсолютные значения максимального и минимального фазового сдвигов, вносимых резонатором, изменяется максимальное значение коэффициента передачи.
Определим комплексный коэффициент передачи резонатора при 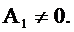 Для этого в выражение для системной функции (2.32) подставим
Для этого в выражение для системной функции (2.32) подставим 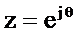 и
и 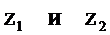 из (2.33)
из (2.33)
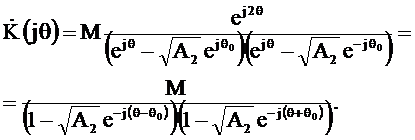 (2.38)
(2.38)
Резонансный коэффициент передачи равен
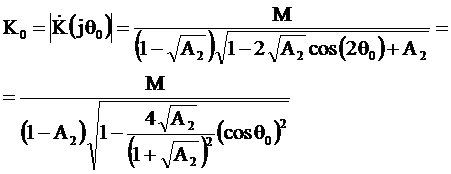 .
.
При 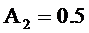 коэффициент перед
коэффициент перед 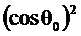 в последнем выражении равен 0.97, при приближении А2 к единице он стремится к единице. Поэтому при
в последнем выражении равен 0.97, при приближении А2 к единице он стремится к единице. Поэтому при 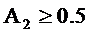 , что, как правило, выполняется в цифровых резонаторах, можно воспользоваться приближённым соотношением
, что, как правило, выполняется в цифровых резонаторах, можно воспользоваться приближённым соотношением
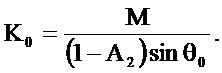 (2.39)
(2.39)
Из (2.39), как частный случай при 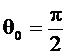 получается (2.37). Из последнего соотношения видно, что минимум резонансного коэффициента передачи при постоянных значениях M и A2 имеет место при
получается (2.37). Из последнего соотношения видно, что минимум резонансного коэффициента передачи при постоянных значениях M и A2 имеет место при 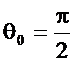 . По мере отклонения резонансной частоты от этого значения резонансный коэффициент передачи увеличивается.
. По мере отклонения резонансной частоты от этого значения резонансный коэффициент передачи увеличивается.
Соотношение (2.39) позволяет определить масштабный коэффициент M, обеспечивающий требуемое значение резонансного коэффициента передачи.
Определим АЧХ резонатора – зависимость модуля комплексного коэффициента передачи (2.38) от частоты
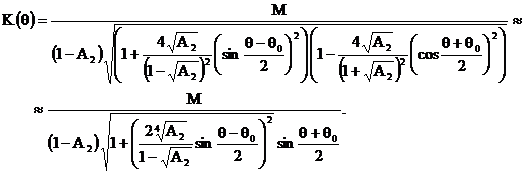
Как и (2.39) последнее соотношение справедливо при 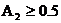 .
.
Разделив 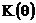 на резонансный коэффициент передачи
на резонансный коэффициент передачи 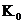 , получим АЧХ в относительном масштабе по оси ординат
, получим АЧХ в относительном масштабе по оси ординат
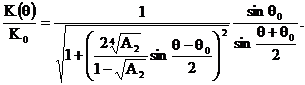
Учитывая, что 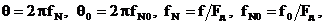 получим АЧХ в относительном масштабе как функцию нормированной частоты
получим АЧХ в относительном масштабе как функцию нормированной частоты 
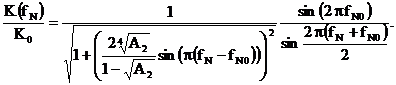 (2.40)
(2.40)
Важным параметром резонатора является полоса пропускания. Рисунок 2.55 иллюстрирует это понятие..
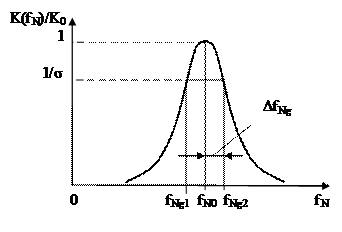
Рисунок 2.55. К определению полосы пропускания
Под нормированной полосой пропускания ПN резонатора понимается разность нормированных граничных частот fNg2-fNg1 вблизи резонансной частоты fN0, определённая на заданном уровне 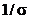 или при заданной допустимой неравномерности в полосе пропускания
или при заданной допустимой неравномерности в полосе пропускания 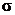 .
.
Под неравномерностью в полосе пропускания понимается отношение максимального коэффициента передачи в пределах полосы пропускания к минимальному. В случае резонатора максимальным является резонансный коэффициент передачи, а минимальным коэффициент передачи на границе полосы пропускания при расстройке относительно резонансной частоты fN0, равной