Первый закон Кирхгофа для мгновенных значений: алгебраическая сумма мгновенных значений токов в узле равна нулю.
,
где k – число ветвей, соединенных в узле.
Второй закон Кирхгофа для мгновенных значений: алгебраическая сумма напряжений на элементах контура в заданный момент времени равна алгебраической сумме ЭДС в том же контуре в тот же момент времени:
,
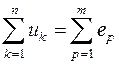где k – порядковый номер напряжения;
p – порядковый номер ЭДС;
n – суммарное число элементов в контуре;
m – число ЭДС в контуре.
1.11 Законы Кирхгофав комплексной форме
Как показано в п. 1.3, синусоидальные функции времени можно представить в комплексной форме. Осуществив подобный переход, можно записать законы Кирхгофа для цепи синусоидального тока в комплексной форме.
Первый закон Кирхгофа в комплексной форме: алгебраическая сумма комплексов токов в узле электрической цепи равна нулю.
,
где k – число ветвей, соединенных в узле.
Например, для цепи, изображенной на рис.1.9, уравнение, составленное по первому закону Кирхгофа в комплексной форме, имеет вид:
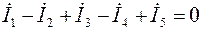
Рисунок 1.9
Второй закон Кирхгофа в комплексной форме: алгебраическая сумма комплексов напряжений в контуре равна алгебраической сумме комплексов ЭДС в этом же контуре.
,
Для контура, изображенного на рис.1.10, уравнение, составленное по второму закону Кирхгофа в комплексной форме, можно записать следующим образом:
,
где 
- комплекс падения напряжения на резисторе R 1;
- комплекс падения напряжения на катушке индуктивности L;
- комплекс падения напряжения на резисторе R 3;
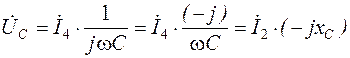- комплекс падения напряжения на конденсаторе С;
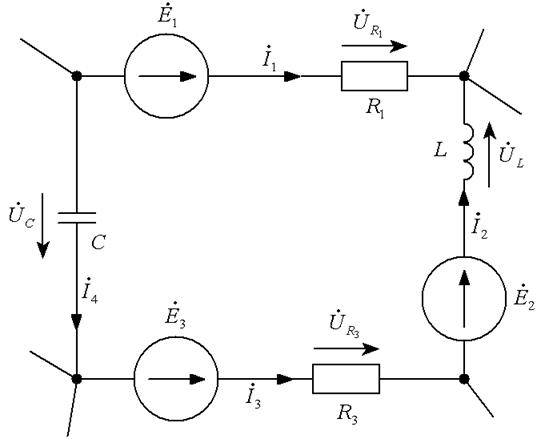
Рисунок 1.10
Пример 7
Определить комплексы токов в ветвях, показания приборов сложной цепи рис.1.11, построить векторную диаграмму токов и напряжений и осциллограмму напряжения на резисторе R 1.
Дано:
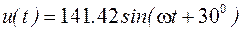(В);
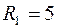(Ом);
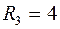(Ом);
(Ом);
(мГн);
(мкФ);
(Гц).
Рисунок 1.11
Решение
Угловая частота колебаний в цепи:
(сек-1)
Определим комплексные сопротивления всех элементов цепи, при этом будем считать, что измерительные приборы идеальные, т.е. сопротивление амперметра равно нулю, а сопротивление вольтметра – бесконечности.
Комплексное сопротивление резистора R 1:
;
Комплексное сопротивление резистора R 2:
;
Комплексное сопротивление катушки индуктивности L:
;
Комплексное сопротивление резистора R 3:
;
Комплексное сопротивление конденсатора С:
;
Комплекс действующего значения напряжения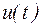 
:
.
Изобразим схему замещения цепи, на которой все элементы цепи и напряжение 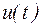заменены их изображениями в комплексной форме (рис.1.12).
Рисунок 1.12
Комплексные сопротивления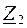 
и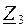 
соединены последовательно, значит их эквивалентное комплексное сопротивление:
;
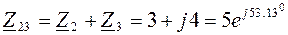Комплексные сопротивления 
и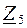 
также соединены последовательно, значит их эквивалентное комплексное сопротивление:
;
Цепь приобретет вид, показанный на рис.1.13.
Рисунок 1.13
Ветви цепи, содержащие комплексные сопротивления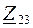 
и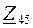 
соединены параллельно, следовательно, эквивалентное комплексное сопротивление участка цепи между узлами a и b:
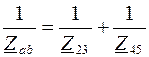или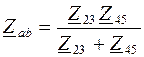 
;
;
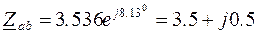После преобразований цепь приобретет вид, показанный на рис.1.14.
Полное эквивалентное комплексное сопротивление цепи рассчитывается как сумма комплексных сопротивлени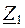й 
и 
:
.
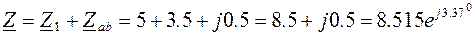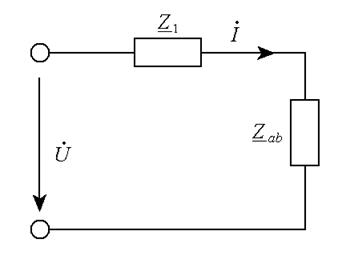
Рисунок 1.14
Определим комплекс действующего значения тока в неразветвленной части цепи:
.
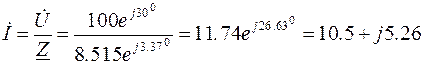Для того, чтобы определить токи в ветвях, содержащих комплексные сопротивления 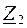, 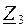и 
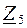, , определим комплекс напряжения между узлами a и b.
Определим комплексы токов в ветвях:
;
;
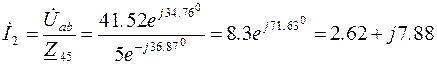Ток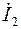 
можно было получить, используя первый закон Кирхгофа:
.
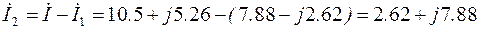Определим показания приборов. Показания приборов представляют собой действующие значения измеряемых величин.
Амперметр показывает действующее значение тока, комплекс которого: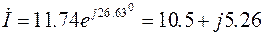 
. Действующее значение – это модуль комплекса тока, т.е. 11.74 (А).
Вольтметр показывает действующее значение напряжения между узлами a и b, комплекс которого: 
. Действующее значение – это модуль комплекса напряжения, т.е. 41.52 (В).
Векторная диаграмма токов представлена на рис.1.15.
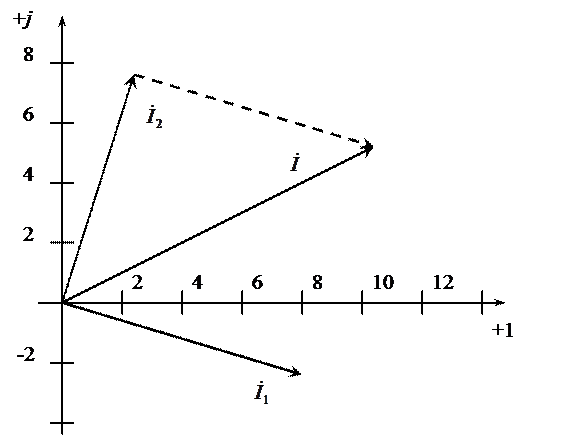
Рисунок 1.15
Для построения векторной диаграммы напряжений определим комплексы напряжений на всех элементах цепи.
Комплекс напряжения на резисторе 
:
(В);
Комплекс напряжения на резисторе 
:
(В);
Комплекс напряжения на катушке индуктивности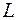 
:
(В);
Комплекс напряжения на резисторе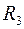 
:
(В);
Комплекс напряжения на конденсаторе 
:
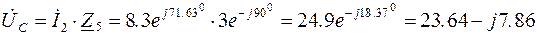(В);
Векторная диаграмма напряжений представлена на рис.1.16.
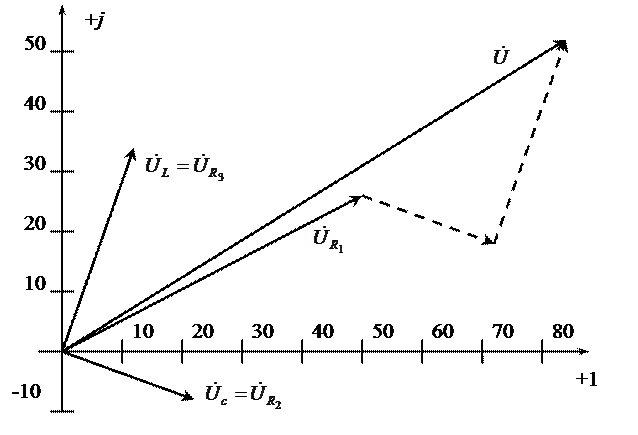
Рисунок 1.16
Для построения осциллограммы напряжения на резисторе R 1 необходимо от найденного нами ранее изображения этого напряжения в комплексной форме 
перейти к ее аналитической форме записи.
Найдем амплитуду этого напряжения:
(В),
Аналитическая зависимость напряжения на резисторе R 1 от времени будет иметь вид (с учетом того, что 
сек-1):
.
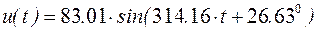Согласно этой формуле осциллограмма будет иметь вид, представленный на рис.1.17.
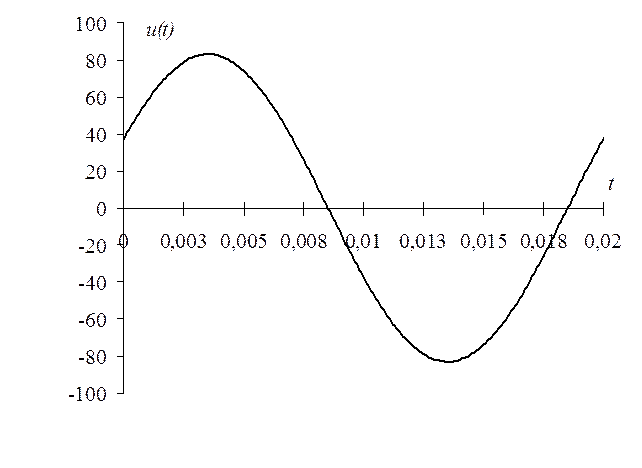
Рисунок 1.17