Уравнение баланса мощностей в цепях синусоидального тока очевидно должно учитывать как мощность, необратимо преобразующуюся в другие виды энергии (активную мощность), так и мощность обратимых преобразований энергии (реактивную мощность). Поэтому уравнения баланса мощностей в цепях синусоидального тока выглядят следующим образом:
Сумма активных мощностей источников энергии равна сумме активных мощностей преемников энергии.
Алгебраическая сумма реактивных мощностей источников энергии равна алгебраической сумме реактивных мощностей преемников энергии. Реактивная мощность может быть положительной (индуктивный элемент) и отрицательной (емкостной элемент).
Пример 9
Составить уравнения баланса мощностей для цепи согласно условию примера 7 (рис.1.18).
Решение
Активная и реактивная мощности, отдаваемые источником энергии, нами найдены (см. пример 8) и так как источник энергии всего один, то:
(Вт);
(вар);
Напряжения и токи на всех участках цепи нами также найдены ранее (см. пример 7).
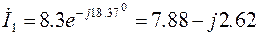(А);
(А),
(А),
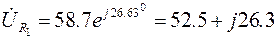(В),
(В),
(В),
(В),
(В).
Найдем комплексно сопряженные токи
(А);
(А);
(А).
Рисунок 1.18
Определим комплексные мощности на каждом из элементов заданной по условию цепи.
Комплексная мощность на резисторе R 1:
;
(Вт); 
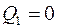(вар);
Комплексная мощность на резисторе R 2:
;
(Вт); 
(вар);
Комплексная мощность на катушке индуктивности L:
;
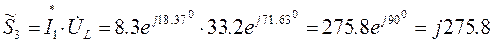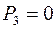(Вт); 
(вар);
Комплексная мощность на резисторе R 3:
;
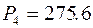(Вт); 
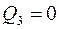(вар);
Комплексная мощность на конденсаторе С:
(Вт); 
(вар);
Определим сумму активных мощностей приемников.
(Вт);
Определим сумму реактивных мощностей приемников.
(вар).
Очевидно, что баланс активных и реактивных мощностей выполняется т.е.
|
|
(Вт);
(вар).
Задание
2.1 Начертить схему замещения электрической цепи с обозначением характера сопротивлений всех ветвей.
2.2 Указать на схеме условные положительные направления токов в ветвях. Определить токи всех ветвей в комплексной форме.
2.3 Определить показания приборов.
2.4 Построить векторную диаграмму токов и напряжений на комплексной плоскости.
2.5 Построить осциллограмму тока в ветви или напряжения на участке, определенном в задании.
2.6 Составить баланс активных и реактивных мощностей.
Исходные данные приведены в таблице 1. Номер схемы для расчётов выбирается из таблицы 1 исходных данных. Номер варианта выбирается согласно номеру по списку в журнале преподавателя.
Значения индуктивностей заданы в микрофарадах (мкФ), емкостей – в милигенри (мГн). Частота тока f = 50 (Гц).
Значения индуктивных и емкостных сопротивлений элементов окркуглять до целого числа.
При составлении баланса активных и реактивных мощностей погрешность вычислений оценить согласно формулам:
;
.
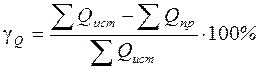Относительная погрешность не должна превышать 5%.
| Таблица 1 | U | u=141sin(ωt) | 180e j45 | u=282sin(ωt) | 60e j30 | 200e j90 | 50e j45 | 100e –j90 | 80e –j90 | 50e j90 | u=113sin(ωt) | 100e j30 | 50e –j60 | 50e –j45 | 220e j30 | 60e –j60 | u=212sin(ωt) | 220e j90 | 120e j30 | 80e j45 | 100e j30 | ||||||||||
| u(t), i(t) | i | u1 | u3 | u1 | i5 | i3 | i4 | u2 | u2 | u2 | i4 | i2 | i3 | u3 | u1 | u3 | i3 | i1 | i2 | u4 | u5 | u4 | i2 | u4 | i1 | u5 | i4 | u5 | i1 | i5 | |
| Z 5 | 3e -j53 | 5e j90 | R=0;C=1062 | -j5 | 10e j30 | 2-j2 | 4+j3 | -j3 | 5e j60 | 5-j3 | 3-j4 | 10e j60 | 8e j30 | R=0;L=25,2 | 4+j4 | R=0;C=318 | 10-j2 | 5e j53 | 2-j2 | R=5;L=6,4 | -j5 | -j3 | R=3;C=1592 | 10e j30 | R=0;C=1062 | 3-j2 | |||||
| Z 4 | 5+j5 | 5-j5 | 3e j90 | R=0;C=1592 | R=2;C=318 | 6+j8 | R=0;L=25,2 | R=0;C=796 | 3+j2 | 5-j5 | 10e –j90 | R=10 | R=0;L=9,6 | -j3 | -j10 | 4-j3 | R=5;C=796 | 3e –j90 | R=0;L=25,2 | R=0;L=6,4 | 10e j90 | 6+j8 | 2-j3 | 5+j5 | 5e j60 | R=0;C=531 | |||||
| Z 3 | J6 | R=0;L=31,8 | j8 | 5e j45 | R=2;C=796 | j6 | 5+j5 | 10e –j53 | 3+j2 | 2+j2 | 2-j3 | -j5 | R=0;L=25,2 | R=0;C=318 | j10 | 5-j5 | 6+j8 | 5e j37 | R=0;C=531 | 8+j6 | R=2;L=31,8 | -j5 | 10-j10 | ||||||||
| Z 2 | R=3;C=318 | J6 | 5+j5 | 10+j10 | 3-j2 | 5e j45 | -j8 | 10-j10 | 3e j60 | 6+j8 | -j10 | 3+j4 | 10+j10 | 10e j45 | 8+j6 | 10e j90 | -j10 | 2+j2 | 10e j37 | 10-j10 | j6 | R=6;L=25,2 | 8-j3 | -j10 | 6+j8 | 6+j5 | 5e –j53 | 3e j60 | |||
| Z 1 | 10+j8 | 10-j8 | j10 | 10e j53 | 3+j4 | 10e –j45 | 8e j53 | 10-j3 | R=0;L=31,5 | 10e –j37 | R=0;C=1062 | j3 | 8e j45 | R=5;C=796 | 10e j90 | j10 | 3-j4 | R=10;L=32 | 3-j4 | R=5;C=795 | 5e j53 | R=0;L=25,2 | 5+j5 | 10e j30 | R=0;C=637 | 5e j53 | 10-j10 | ||||
| № рисунка | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 2.10 | 2.11 | 2.12 | 2.13 | 2.14 | 2.15 | 2.16 | 2.17 | 2.18 | 2.19 | 2.20 | 2.21 | 2.22 | 2.23 | 2.24 | 2.25 | 2.26 | 2.27 | 2.28 | 2.1 | 2.2 | |
| № группы | |||||||||||||||||||||||||||||||
| № вар. |
|
|
| Продолжение таблицы 1 | U | 60ej90 | u=282sin(ωt) | u=141sin(ωt-π/2) | 120ej30 | 50ej45 | u=255sin(ωt) | 60ej90 | u=235sin(ωt) | 60ej90 | 100e-j30 | u=282sin(ωt+π/2) | 50ej30 | 100ej60 | 100e-j60 | u=141sin(ωt-π/3) | 60ej30 | u=212sin(ωt) | 60e-j30 | 220ej60 | |||||||||||
| u(t), i(t) | u4 | i5 | u3 | i4 | u2 | u2 | u3 | i3 | u4 | i2 | i4 | u2 | u5 | i1 | u3 | u5 | u4 | i5 | u3 | i4 | u2 | u2 | u3 | i3 | u4 | i2 | i4 | u2 | u5 | i1 | |
| Z 5 | 4+j4 | 10+j10 | 5ej90 | j10 | 6+j8 | 8ej30 | j10 | -j8 | 8-j8 | 5+j3 | R=5;C=637 | R=0;L=6,4 | j5 | 2-j10 | 2+j2 | 3e-j90 | R=0;C=637 | -j3 | 8ej30 | R=0;L=31,8 | j5 | 3+j4 | R=0;L=6,5 | 8+j8 | -j5 | 5ej45 | |||||
| Z 4 | 10ej90 | R=0;C=318 | -j10 | 5+j5 | 3-j4 | 5ei53 | 6+j8 | 3+j2 | 3+j2 | 8ej45 | -j8 | R=0;L=25,2 | 8ej30 | 10+j8 | 5ej90 | 5+j3 | -j5 | 10ej45 | 3ej30 | 8-j3 | 3ej90 | R=0;L=25,2 | R=2;C=1443 | 2-j3 | 8+j8 | -j6 | |||||
| Z 3 | j10 | 3-j4 | 10ej50 | 10-j3 | 3-j4 | R=10;C=318 | 8-j6 | 10-j2 | R=0;C=1592 | 10-j5 | 3-j3 | R=5;L=15,9 | 10ej30 | 6+j8 | j6 | 3+j2 | R=0;C=796 | 5ej53 | 2+j2 | R=0;L=9,6 | 5+j5 | j6 | 3+j2 | R=0;C=1062 | -j5 | 3+j3 | |||||
| Z 2 | 4-j3 | R=10;C=796 | 6+j8 | 3+j4 | R=5;L=15,9 | R=0;L=6,4 | -j5 | 10+j10 | 10ej37 | 5e-j90 | R=0;L=31,8 | j5 | R=10;C=318 | -j5 | 5-j4 | 10ej90 | 8+j6 | 5+j5 | -j8 | R=6;L=25,2 | 3e-j90 | -j10 | j5 | -j8 | 3ej60 | 10e-j90 | 10ej53 | 8ej60 | |||
| Z 1 | R=0;C=318 | j10 | 10ej37 | 10ej90 | 2+j3 | 2-j3 | 5ej90 | 2-j2 | R=3;L=9,6 | 5+j5 | 3ej5 | 10ej90 | 3-j2 | R=0;L=6,4 | 3-j4 | 5ej30 | R=10;C=318 | 8ej45 | 5-j5 | 1010-j2 | 10-j2 | 2+j2 | R=0;L=15,9 | 10ej30 | R=0;C=318 | 6ej90 | 4+j3 | ||||
| № рисунка | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 2.10 | 2.11 | 2.12 | 2.13 | 2.14 | 2.15 | 2.16 | 2.17 | 2.18 | 2.19 | 2.20 | 2.21 | 2.22 | 2.23 | 2.24 | 2.25 | 2.26 | 2.27 | 2.28 | 2.1 | 2.2 | 2.3 | 2.4 | |
| № группы | |||||||||||||||||||||||||||||||
| № вар. |
|
|
| Окончание таблицы 1 | U | 100e45 | u=282sin(ωt+π/3) | 150e90 | u=141sin(ωt-π/3) | 212sin(ωt) | 120e-j30 | 50e-j45 | u=71sin(ωt+ π/4) | u=85sin(ωt+ 300) | 100e-j90 | |||||||||
| u(t), i(t) | u3 | i4 | u2 | u2 | u3 | i3 | u4 | i2 | i4 | u2 | u5 | i1 | u3 | u5 | u4 | |||||
| Z 5 | R=3;L=9,6 | 8ej45 | 10e-j45 | -j3 | R=10;C=318 | 5ej53 | 5+j5 | -j5 | j3 | R=0;C=318 | 3ej45 | |||||||||
| Z 4 | -j3 | 5+j3 | 8ej90 | R=0;L=25,2 | 5-j5 | 8ej30 | R=0;C=796 | -j5 | 10ej90 | 5ej60 | 6+j8 | R=0;C=318 | 8+j6 | -j10 | ||||||
| Z 3 | 10ej45 | 10+j10 | -j5 | j6 | 3+j2 | -j5 | 6+j8 | R=0;L=25,2 | 10+j10 | R=3;C=1062 | -j5 | 6+j6 | -j5 | R=2;L=25,2 | ||||||
| Z 2 | 5+j5 | R=0;C=318 | 3+j4 | 10-j10 | -j8 | 10ej45 | 10ej37 | j6 | 5e-j53 | j8 | 10ej45 | 5+j5 | ||||||||
| Z 1 | R=0;C=398 | 6ej90 | 4+j3 | 8ej53 | 10ej37 | j5 | 3-j4 | 8ej45 | 3-j5 | R=0;C=796 | 10-j10 | 3-j4 | 10e-j45 | j3 | -j8 | |||||
| № рисунка | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 2.10 | 2.11 | 2.12 | 2.13 | 2.14 | 2.15 | 2.16 | 2.17 | 2.18 | 2.19 | |||||
| № группы | ||||||||||||||||||||
| № вар. | ||||||||||||||||||||
Рисунок 2.1
| ||||||||||||||||||||
Рисунок 2.2
| ||||||||||||||||||||
Рисунок 2.3
| ||||||||||||||||||||
Рисунок 2.4
| ||||||||||||||||||||
Рисунок 2.5
| ||||||||||||||||||||
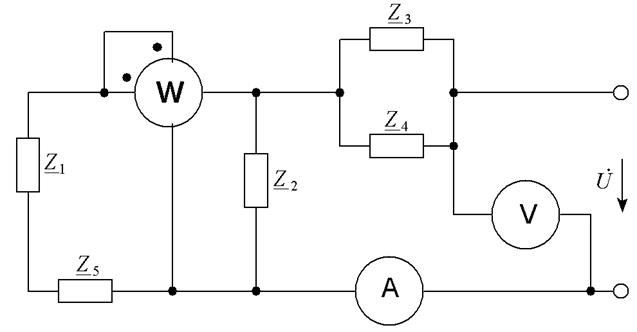Рисунок 2.6
| ||||||||||||||||||||
Рисунок 2.7
| ||||||||||||||||||||
Рисунок 2.8
| ||||||||||||||||||||
Рисунок 2.9
| ||||||||||||||||||||
Рисунок 2.10
| ||||||||||||||||||||
Рисунок 2.11
| ||||||||||||||||||||
Рисунок 2.12
| ||||||||||||||||||||
Рисунок 2.13
| ||||||||||||||||||||
Рисунок 2.14
| ||||||||||||||||||||
Рисунок 2.15
| ||
Рисунок 2.16
| ||
Рисунок 2.17
| ||
Рисунок 2.18
| ||
Рисунок 2.19
| ||
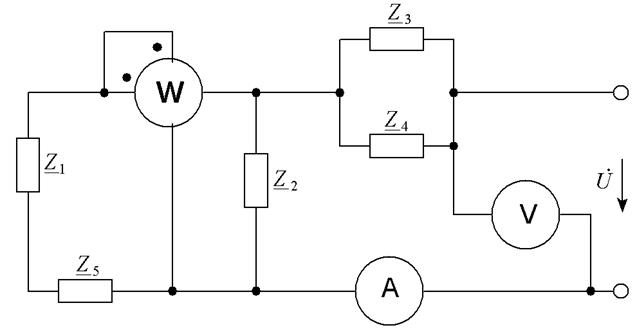Рисунок 2.20
| ||
Рисунок 2.21
| ||
Рисунок 2.22
| ||
Рисунок 2.23
| ||
Рисунок 2.24
| ||
Рисунок 2.25
| ||
Рисунок 2.26
| ||
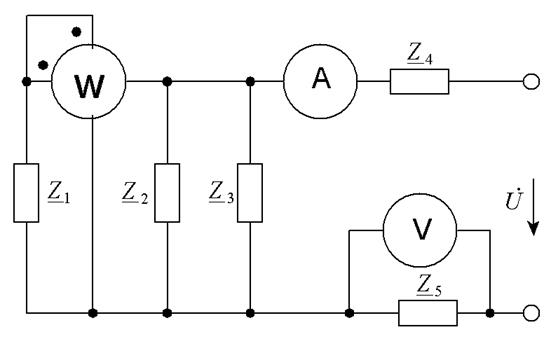Рисунок 2.27
| ||
Рисунок 2.28
|