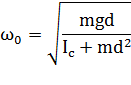Гармонические колебания
План:
1. Понятие о механических колебаниях.
2. Характеристика механических колебаний.
Колебаниями, или колебательными процессами, называются процессы, в которых значения параметров состояния системы периодически повторяются. Такими свойствами обладают, например, качание маятника часов, колебания ножек камертона или струны, напряжение между обкладками конденсатора в контуре радиоприемника и т.д.
Механическими колебаниями называются периодические (или почти периодические) изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т.п.). Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени 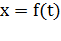 . Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени (рис. 7.1.1).
. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени (рис. 7.1.1).

|
| Рис. 7.1.1. Механические колебательные системы. |
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными.
Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением:
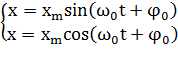
где  – смещение тела от положения равновесия,
– смещение тела от положения равновесия, 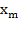 – амплитуда колебаний, т.е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний,
– амплитуда колебаний, т.е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний,  – время. Величина, стоящая под знаком косинуса
– время. Величина, стоящая под знаком косинуса 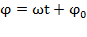 называется фазой гармонического процесса. При
называется фазой гармонического процесса. При 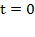
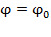 , поэтому
, поэтому 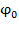 называют начальной фазой.
называют начальной фазой.
|
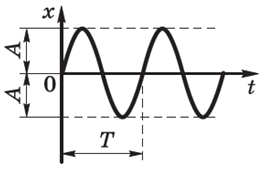
| Рис. 7.1.2. График колебательного движения |
Амплитудой называют скалярную физическую величину, численно равную модулю максимального смещения тела от положения равновесия при колебательном движении.
Период колебаний время совершения одного полного колебания при колебательном движении тела. Единицей периода является секунда (с).

Частота колебаний – скалярная физическая величина, равная числу колебаний в единицу времени:
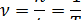
Циклическая частота – скалярная физическая величина, равная числу колебаний в 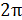 единиц времени:
единиц времени:
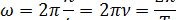
Свободные колебания. Пружинный и математический маятник
План:
1. Свободные колебания. Характеристика свободных колебаний.
2. Пружинный и математический маятник.
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.
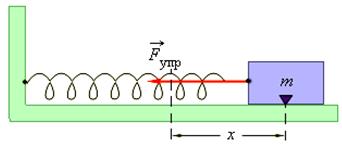
|
| Рис. 7.2.1. Колебания груза на пружине. Трения нет. |
Таким образом, груз некоторой массы  , прикрепленный к пружине жесткости
, прикрепленный к пружине жесткости 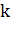 , второй конец которой закреплен неподвижно (рис. 7.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.
, второй конец которой закреплен неподвижно (рис. 7.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.
Круговая частота 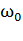 свободных колебаний груза на пружине находится из второго закона Ньютона:
свободных колебаний груза на пружине находится из второго закона Ньютона: 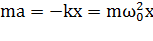 ,
,
откуда: 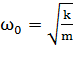 .
.
Частота 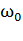 называется собственной частотой колебательной системы.
называется собственной частотой колебательной системы.
Период 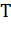 гармонических колебаний груза на пружине равен:
гармонических колебаний груза на пружине равен:

При горизонтальном расположении системы пружина – груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину  , равную:
, равную: 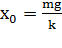 и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты
и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты 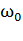 и периода колебаний T справедливы и в этом случае.
и периода колебаний T справедливы и в этом случае.
Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела 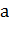 и координатой
и координатой  : ускорение является второй производной координаты тела
: ускорение является второй производной координаты тела  по времени
по времени  :
: 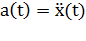 .
.
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде: 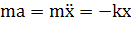 или
или 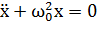 (*),
(*),
где 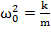 .
.
Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида:
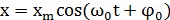
Уравнение (*) называется уравнением свободных колебаний. Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний 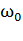 или период T. Такие параметры колебательного процесса, как амплитуда
или период T. Такие параметры колебательного процесса, как амплитуда 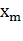 и начальная фаза
и начальная фаза 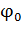 , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.
, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.
Если, например, груз был смещен из положения равновесия на расстояние 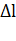 и затем в момент времени
и затем в момент времени 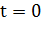 отпущен без начальной скорости, то
отпущен без начальной скорости, то 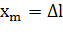 ,
, 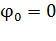 .
.

|
| Рис. 7.2.2. Крутильный маятник. |
Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость 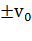 то
то 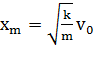 ,
, 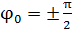 .
.
Таким образом, амплитуда 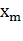 свободных колебаний и его начальная фаза
свободных колебаний и его начальная фаза 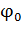 определяются начальными условиями.
определяются начальными условиями.
Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 7.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс.
При повороте диска на угол θ возникает момент сил 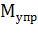 упругой деформации кручения:
упругой деформации кручения: 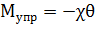 .
.
Это соотношение выражает закон Гука для деформации кручения. Величина 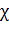 аналогична жесткости пружины
аналогична жесткости пружины 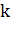 . Второй закон Ньютона для вращательного движения диска записывается в виде:
. Второй закон Ньютона для вращательного движения диска записывается в виде:
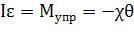 или
или 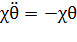
где 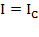 – момент инерции диска относительно оси, проходящий через центр масс,
– момент инерции диска относительно оси, проходящий через центр масс,
ε – угловое ускорение.
По аналогии с грузом на пружине можно получить: 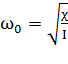 ;
; 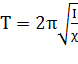 .
.
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки.
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести 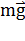 уравновешивается силой натяжения нити
уравновешивается силой натяжения нити 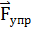 . При отклонении маятника из положения равновесия на некоторый угол
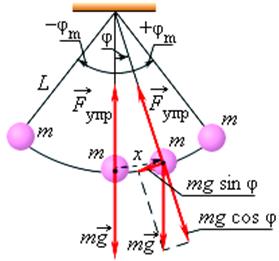
. При отклонении маятника из положения равновесия на некоторый угол 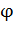 появляется касательная составляющая силы тяжести
появляется касательная составляющая силы тяжести 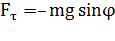 (рис. 7.2.3). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
(рис. 7.2.3). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
|
Рис. 7.2.3. Математический маятник: 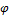 – угловое отклонение маятника от положения равновесия, – угловое отклонение маятника от положения равновесия, 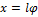 – смещение маятника по дуге. – смещение маятника по дуге.
|
Если обозначить через  линейное смещение маятника от положения равновесия по дуге окружности радиуса
линейное смещение маятника от положения равновесия по дуге окружности радиуса  , то его угловое смещение будет равно
, то его угловое смещение будет равно 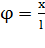 . Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:
. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает: 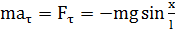 .
.
Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x, а 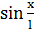 .
.
Только в случае малых колебаний, когда приближенно 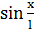 можно заменить на
можно заменить на 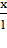 , математический маятник является гармоническим осциллятором, т.е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15 – 20°; при этом величина
, математический маятник является гармоническим осциллятором, т.е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15 – 20°; при этом величина 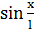 отличается от
отличается от 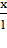 не более чем на 2%. Колебания маятника при больших амплитудах не являются гармоническими.
не более чем на 2%. Колебания маятника при больших амплитудах не являются гармоническими.
Для малых колебаний математического маятника второй закон Ньютона записывается в виде: 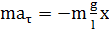 .
.
Таким образом, тангенциальное ускорение 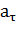 маятника пропорционально его смещению
маятника пропорционально его смещению  , взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:
, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:
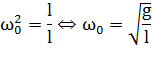
Эта формула выражает собственную частоту малых колебаний математического маятника.
Следовательно:
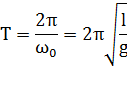

|
| Рис. 7.2.4. Физический маятник. |
Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 7.2.4). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол 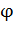 возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:
возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:
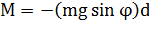
где: d – расстояние между осью вращения и центром масс C.
Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент 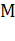 пропорционален
пропорционален 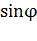 . Это означает, что только при малых углах
. Это означает, что только при малых углах 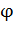 , когда
, когда 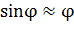 , физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний:
, физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний: 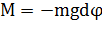 и второй закон Ньютона для физического маятника принимает вид:
и второй закон Ньютона для физического маятника принимает вид:
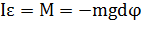
где ε – угловое ускорение маятника,
I – момент инерции маятника относительно оси вращения O.
Модуль коэффициента пропорциональности между ускорением и смещением равен квадрату круговой частоты: 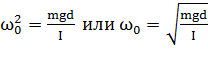 ,
,
где 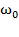 – собственная частота малых колебаний физического маятника.
– собственная частота малых колебаний физического маятника.
Следовательно:
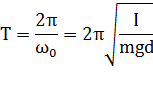
Более строгий вывод формул для 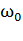 и
и 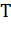 можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение
можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение 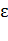 есть вторая производная углового смещения
есть вторая производная углового смещения 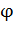 по времени:
по времени: 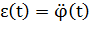 .
.
Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде: 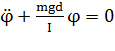 .
.
Это уравнение свободных гармонических колебаний. Коэффициент 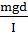 в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.
в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.
По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции  можно выразить через момент инерции
можно выразить через момент инерции 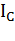 относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:
относительно оси, проходящей через центр масс C маятника и параллельной оси вращения: 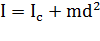 . Окончательно для круговой частоты
. Окончательно для круговой частоты 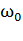 свободных колебаний физического маятника получается выражение:
свободных колебаний физического маятника получается выражение: