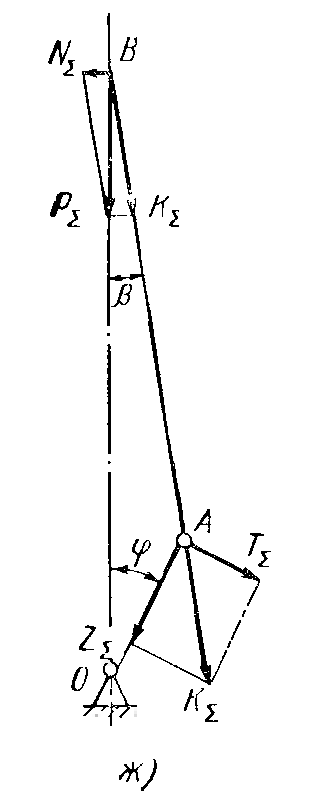
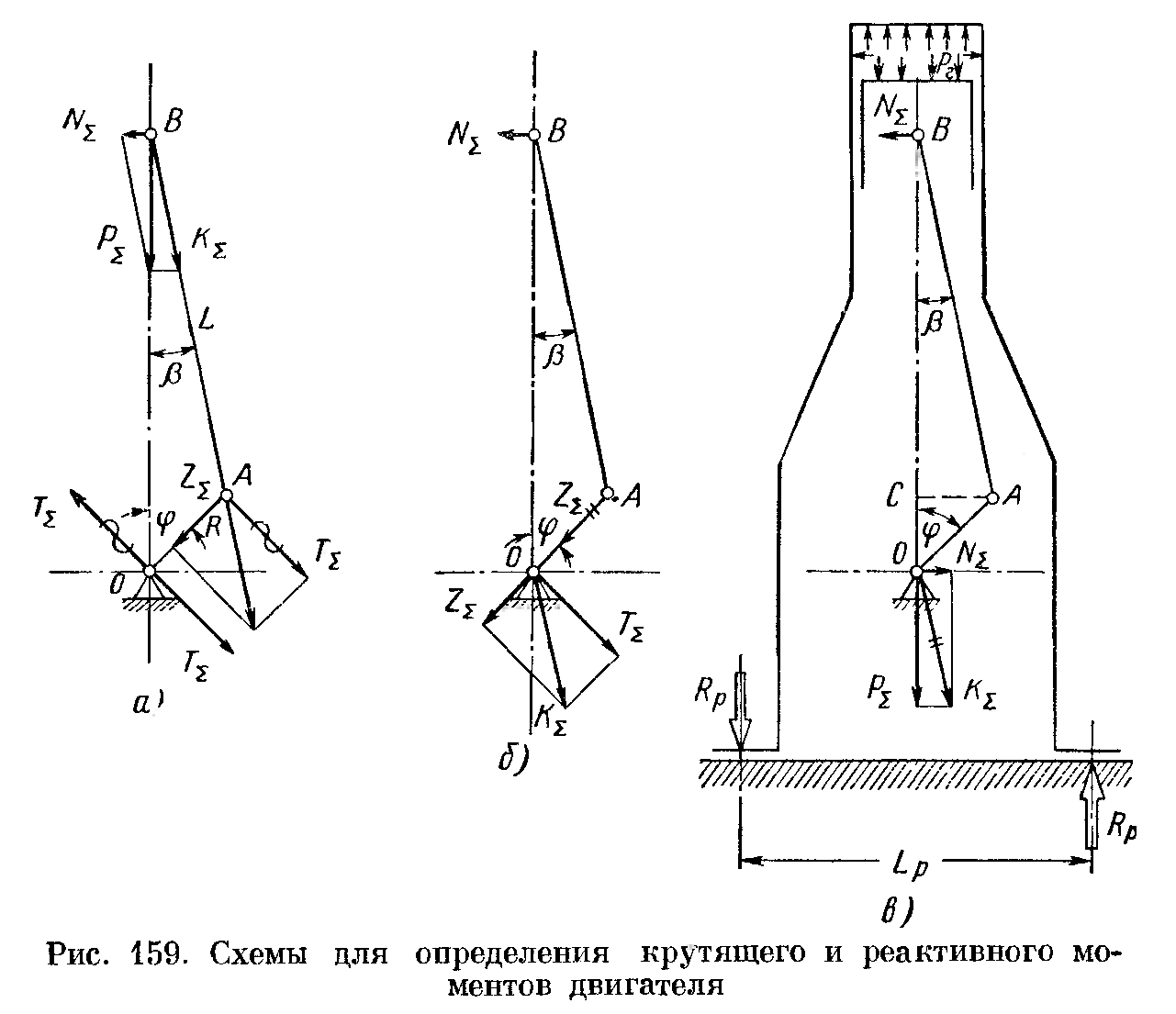
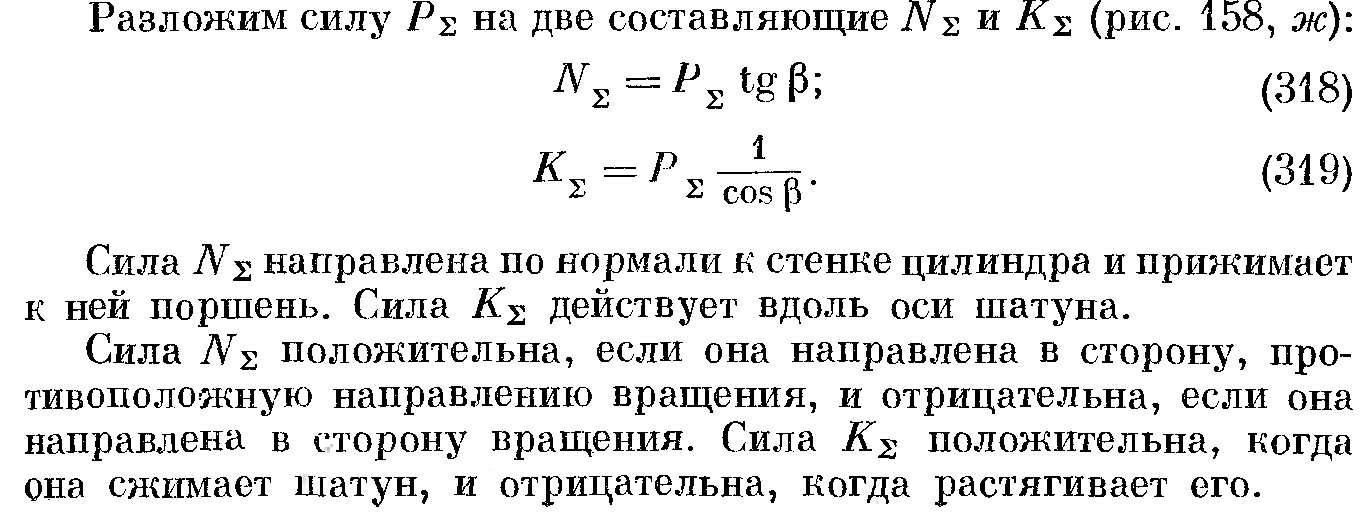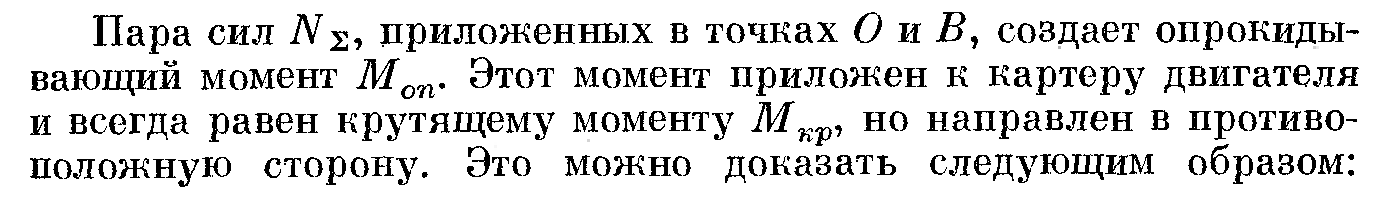При работе двигателя на кривошипно-шатунный механизм действуют силы давления газов и силы инерции. Силы инерции масс кривошипно-шатунного механизма, движущихся с переменными по величине и направлению скоростями, возникают на всех режимах работы двигателя и для некоторых деталей этого механизма являются основными расчётными силами. Это связано с тем, что в высокооборотных двигателях силы инерции значительно превосходят силы газов и поэтому являются основными при расчёте деталей на усталостную прочность.
В зависимости от характера движения силы инерции масс КШМ делятся на:
- силы инерции масс, движущихся возвратно-поступательно;
- силы инерции вращающихся масс;
- силы инерции масс, совершающих сложное движение;
Для определения этих сил необходимо знать соответствующие массы.
Приведение массы шатуна.
Шатун совершает сложное поступательно-качательное движение в плоскости, перпендикулярной к оси коленчатого вала. При приведении массы шатуна к трем массам одну из них сосредотачивают на оси верхней головки шатуна, другую – на оси нижней головки шатуна, а третью – в центре тяжести шатуна. (рис. 5)
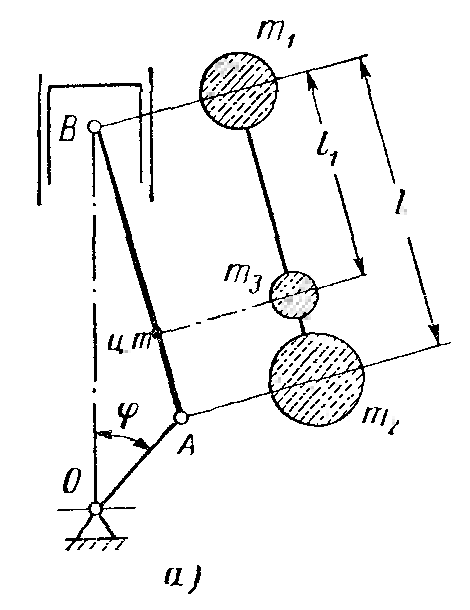
1) mш = m1 + m2 + m3;
2) m1l1 = m2(l – l1);
3) Jш = m1l12 + m2(l – l1)2;
где Jш - момент инерции шатуна.
| Рисунок 5 |
Приведение вращающихся масс.
К вращающимся массам КШМ относятся масса неуравновешенных частей кривошипа тк и часть массы шатуна т2.
Массу неуравновешенных частей кривошипа приводят к оси шатунной шейки. При этом центробежная сила приведённой массы тк должна быть равна сумме центробежных сил всех неуравновешенных частей кривошипа при условии постоянства угловой скорости вращения ω.
При наличии в колене вала противовесов их массу также следует привести к оси шатунной шейки.
тR = тк + т2.
Масса частей, движущихся возвратно-поступательно
Масса частей КШМ, движущихся возврато-поступательно
т = тп + т1,
где тп – масса комплектного поршня, включащая массы собственно поршня, поршневых колец, поршневого пальца и заглушек или стопорных колец;
т1 – часть массы шатуна, отнесённая к оси поршневого пальца.
Массу т полагают сосредоточенной в центре пальца поршня.
2.1 Сила инерции Р ω масс, движущихся возвратно-поступательно
Рω = РωI + РωII,
где РωI - сила инерции первого порядка, период изменения этой силы – один оборот колечатого вала;
РωII - сила инерции второго порядка, период изменения этой силы – полоборота коленчатого вала;
2.2 Сила инерции Р R вращающихся масс
Сила инерции вращающихся масс действует по радиусу кривошипа и определяется по формуле
РR = - тRRω2 = const.
2.3 Сила давления газов
Закон изменения давленя газов на поршень по его ходу или углу поворота коленчатого вала обычно задаётся индикаторной диаграммой.
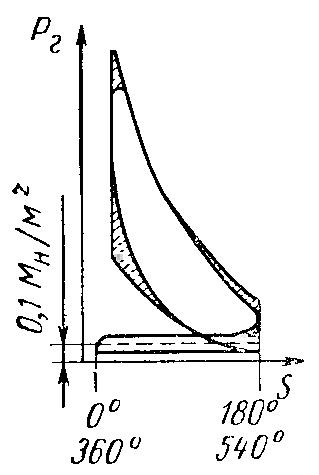
2.4 Суммарные силы, действующие в КШМ
Суммарная сила, действующая по оси цилиндра, складывается из силы избыточного давления газов на поршень и силы инерции масс, движущихся возврано-поступательно
Р∑ = Рг + Рω