Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). 
Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом). Методы оптимизации классифицируют в соответствии с задачами оптимизации:
- Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.
- Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.
Существующие в настоящее время методы поиска можно разбить на три большие группы:
1. детерминированные;
2. случайные (стохастические);
3. комбинированные.
По критерию размерности допустимого множества, методы оптимизации делят на методы одномерной оптимизации и методы многомерной оптимизации.
По виду целевой функции и допустимого множества, задачи оптимизации и методы их решения можно разделить на следующие классы:
- Задачи оптимизации, в которых целевая функция f (x →) {\displaystyle f({\vec {x}})} f(x)и ограничения g i (x →), i = 1, …, m {\displaystyle g_{i}({\vec {x}}),\;i=1,\ldots,m} gi(x), i=1,...,m являются линейными функциями, разрешаются так называемыми методами линейного программирования.
- В противном случае имеют дело с задачей нелинейного программирования и применяют соответствующие методы. В свою очередь из них выделяют две частные задачи:
-
если f (x →) {\displaystyle f({\vec {x}})} f(x) и g i (x →), i = 1, …, m {\displaystyle g_{i}({\vec {x}}),\;i=1,\ldots,m} gi(x), i=1,...,m — выпуклые функции, то такую задачу называют задачей выпуклого программирования; - если X ⊂ Z {\displaystyle \mathbb {X} \subset \mathbb {Z} }X∁Z, то имеют дело с задачей целочисленного (дискретного) программирования.
По требованиям к гладкости и наличию у целевой функции частных производных, их также можно разделить на:
- прямые методы, требующие только вычислений целевой функции в точках приближений;
- методы первого порядка: требуют вычисления первых частных производных функции;
- методы второго порядка: требуют вычисления вторых частных производных, то есть гессиана целевой функции.
Помимо того, оптимизационные методы делятся на следующие группы:
- аналитические методы (например, метод множителей Лагранжа и условия Каруша — Куна — Таккера);
- численные методы;
- графические методы.
В зависимости от природы множества X задачи математического программирования классифицируются как:
- задачи дискретного программирования— если X конечно или счётно;
- задачи целочисленного программирования — если X является подмножеством множества целых чисел;
- задачи нелинейного программирования, если ограничения или целевая функция содержат нелинейные функции и X является подмножеством конечномерного векторного пространства.
- Если же все ограничения и целевая функция содержат лишь линейные функции, то это — задача линейного программирования.
Кроме того, разделами математического программирования являются параметрическое программирование, динамическое программирование и стохастическое программирование.
Математическое программирование используется при решении оптимизационных задач исследования операций.
Способ нахождения экстремума полностью определяется классом задачи. Но перед тем, как получить математическую модель, нужно выполнить 4 этапа моделирования:
- Определение границ системы оптимизации
- Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а, точнее, те, без которых решение упрощается
- Выбор управляемых переменных
- «Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные)
- Определение ограничений на управляемые переменные
- … (равенства и/или неравенства)
- Выбор числового критерия оптимизации (например, показателя эффективности).
2.1 Метод сканирования
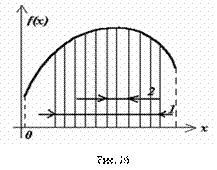
Метод заключается в последовательном переборе всех значений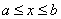 
С шагом e (погрешность решения) с вычислением критерия оптимальности F в каждой точке. Путем выбора наибольшего из всех вычислений значений F и находится решение задачи Х*.
Достоинство метода в том, что можно найти глобальный максимум критерия, если F(X) – многоэкстремальная функция. К недостаткам данного метода относится значительное число повторных вычислений F(X), что в случае сложной функции F(X) требует существенных затрат времени.
На практике можно реализовать одну из основных модификаций метода – последовательное уточнение решения, или сканирование с переменным шагом (рис. 16). Рассмотрим иллюстрацию модифицированного метода сканирования:
1 – интервал, включающий в себя искомый максимум функции после первого этапа сканирования (исходный участок разбит на 5 участков);
2 – то же после второго этапа.
На первом этапе сканирование осуществляют с крупным шагом, затем отрезок, внутри которого получено наибольшее значение F(х), Разбивается на более мелкие отрезки, ищется новый отрезок, внутри которого уточненное значение максимума. Он (новый отрезок) опять делится на более мелкие и т. 
д., тех пор, пока величина отрезка, содержащего максимальное значение F(X), не будет меньше заданной погрешности. Главный недостаток этого варианта метода – возможность пропуска «острого» глобального максимума F(X).
2.2 Одномерная безусловная оптимизация
Задачи безусловной одномерной минимизации представляют собой простейшую математическую модель оптимизации, в которой целевая функция зависит от одной переменной, а допустимым множеством является отрезок вещественной оси:
f(x)→min, x є[a;b].
К математическим задачам одномерной минимизации приводят прикладные задачи оптимизации с одной управляемой переменной. Кроме того минимизация функций одной переменной является как правило
необходимым элементом многих методов минимизации многомерных функция безусловной и условной оптимизации.
На первый взгляд кажется, что задача минимизации функции одной переменной является довольно элементарной. В самом деле, если функция f(x), которую нужно минимизировать на отрезке [a;b], дифференцируема, то достаточно найти нули производной, присоединить к ним концы отрезка, выделить из этих точек локальные минимумы и, наконец, среди последних найти ту точку, в которой достигается абсолютный минимум.
Однако для широкого класса функций эта задача не так уж проста. Во-первых, задача решения уравнения f(x)=0 может оказаться, как это и бывает в отдельных ситуациях, весьма сложной. С другой стороны, в практических задачах часто не известно, является ли функция дифференцируемой. Ввиду этого существенное значение приобретают методы оптимизации не требующие вычисления производной.
Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации. Большим достоинством прямых методов является то, что от целевой
функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f(x) в заданных точках. Методами поиска определяется достаточно малый интервал, в котором находится минимум, осуществляя при этом наименьшее количество вычислений функции (так как затраты на вычисления могут быть весьма велики).
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Так как для приближенного определение точки оптимума исследуют поведение функции в конечном числе точек, то методы отличаются друг от друга лишь способом выбора этих точек. Суть методов состоит в построении последовательности отрезков стягивающихся к точке минимума.
Самым слабым требованием на функцию f(x), позволяющим использовать эти методы, является её унимодальность, то есть функция имеет на заданном отрезке только одну точку минимума. Прежде, чем применять эти методы, необходимо выделить интервал, содержащий точку минимума, и убедиться, что она там единственная. В противном случае предлагаемые методы будут определять только один локальный минимум.
2.3 Многомерная безусловная оптимизация
Постановка задач многомерной оптимизации При математической формулировке задачи условной оптимизации целевую функцию выбирают с таким знаком, чтобы решение задачи соответствовало поиску минимума этой функции. Поэтому формулировку общей задачи математического программирования обычно записывают так:
f(x)→min (1.1)
Q
где QÌRN — множество возможных альтернатив, рассматриваемых при поиске решения задачи. Любую точку xÎQ называют допустимым решением задачи математического программирования, а само множество — множеством допустимых решений или, короче, допустимым множеством. Точку x*, в которой функция f (x) достигает своего наименьшего значения, называют оптимальным решением задачи.
При отсутствии ограничений множество Q совпадает с областью определения целевой функции. Если же рассматриваемые альтернативы
должны удовлетворять некоторым ограничениям, то множество допустимых решений сужается.
Задачу (1.1) в дальнейшем будем называть задачей минимизации целевой функции на множестве Q, a целевая функция может и не достигать на Q наименьшего значения. Тогда говорят о точной нижней грани функции f (x) r на этом множестве и вместо (1.1) используют запись
f (x) ® inf, xÎ Q (1.2)
Отличие (1.1) от (1.2) в том, что в первом случае предполагают существование точки x *, в которой целевая функция достигает своего наименьшего значения на множестве Q, а во втором случае такая точка может и не существовать. Поэтому решение общей задачи математического программирования состоит в том, чтобы в первом случае найти точные (или с некоторой заданной точностью) значения координат точки
x*={xj}j=1…N и значение целевой функции f (x*) min f(x). Во втором случае построить такую последовательность точек {xn}nÎN которой бы соответствовала последовательность f(xn), сходящаяся к значению inf f (x), и вычислить это значение с заданной точностью. Отметим, что в большинстве прикладных задач имеет место первый случай, поэтому использование записи вида (1.2) будем оговаривать особо.
Сформулируем задачу многомерной безусловной оптимизации: найти минимум функции f (x), где xÎRN при отсутствии ограничений на x, при этом f(x) – это скалярная целевая функция, непрерывно дифференцируемая.
При решении этого класса задача необходимо учитывать следующие факторы:
- характер целевой функции решаемой задачи;
- возможность получения в процессе оптимизации информации о производных- целевой функции;
- наличие различных подходов к организации итеративной процедуры- поиска оптимума (методы, основанные на итеративном движении переменных в направлении, определяемом тем или иным способом).
Все методы решения задач безусловной оптимизации состоят в том, что мы строим последовательность точек {x(n)} таким образом, чтобы последовательность функций f(x(n)) была убывающей (т. е. спускаемся вдоль функции). На k-м шаге (k>0) определяем вектор Sk, в направлении которого функция f (x) уменьшается. В этом направлении делаем шаг величиной lk и получаем новую точку, xk+1=xk+lkSk , в которой f(xk+1)<f(xk). Последовательность, {x(n)}nÎN удовлетворяющая этому условию, 
называется релаксационной последовательностью, а соответствующие методы – методами спуска. Методы решения делятся на методы с использованием информации о производных функции и без использования таковой. Различные методы спуска отличаются выбором направления и величины шага. Как правило, для нахождения lk используется процедура одномерного поиска.
 |
3 Описание команд MatLab
3.1. Команда MatLab plot3:
Синтаксис:
plot3(x, y, z)
plot3(x, y, z, s)
plot3(x1, y1, z1, s1, x2, y2, z2, s2,...)
Описание:
Команды plot3(...) являются трехмерными аналогами функции plot(...).
Команда plot3(x, y, z), где x, y, z - одномерные массивы одинакового размера, строит точки с координатами x(i), y(i), z(i) и соединяет их прямыми линиями.
Команда plot3(x, y, z, s) позволяет выделить график функции z(x, y), указав способ отображения линии, способ отображения точек, цвет линий и точек с помощью строковой переменной s, которая может включать до трех символов из следующей таблицы 1.
Таблица 1
| Тип линии | Тип точки | Цвет | ||||||||||||||||||||||||||||||||||
|
|
|
Если цвет линии не указан, он выбирается по умолчанию из шести первых цветов, с желтого до синего, повторяясь циклически.
Команда plot3(x1, y1, z1, s1, x2, y2, z2, s2,...) позволяет объединить на одном графике несколько функций z1(x1, y1), z2(x2, y2),..., определив для каждой из них свой способ отображения.
Обращение к команде plot3 вида plot3(x, y, z, s1, x, y, z, s2) позволяет для графика z(x, y) определить дополнительные свойства, для указания которых применения одной строковой переменной s1 недостаточно, например при задании разных цветов для линии и для точек на ней.
3.2. Команда MatLab contour.
Синтаксис:
| contour(Z) | contour(x,y,Z) | |
| contour(Z, n) | contour(x,y,Z,n) | |
| contour(Z, v) | contour(x,y,Z,v) | |
| contour(...,’тип_линии’) | ||
| C = contour(...) | ||
| [C, h] = contour(...) |
Описание:
Команда contour(Z) рисует двумерные линии уровня для массива данных Z, определяющих поверхность в трехмерном пространстве без учета диапазона изменения координат x и y.
Команда contour(x, y, Z), где x и y - векторы, рисует линии уровня для массива данных Z с учетом диапазона изменения координат x и y.
Команды contour(Z, n), contour(x, y, Z, n) рисует n линий уровня для массива данных Z; по умолчанию, n равно 10.
Команды contour(Z, v), contour(x, y, Z, v) рисуют линии уровня для заданных значений, которые указаны в векторе v.
Команда contour(...,’<тип линии>’) рисует линии уровня, тип и цвет которых определяются параметром <тип линии> команды plot.
Функция C = contour(...) возвращает массив C описания линий уровней по аналогии с функцией contourc для последующего использования командой clabel.
Функция [C, h] = contour(...) возвращает массив C и вектор-столбец дескрипторов h графических объектов line для каждой линии уровня.
3.3. Команда MatLab meshgrid.
Формирование узлов двухмерной и трехмерной сеток.
| Синтаксис: [X, Y] = meshgrid(x, y) [X, Y] = meshgrid(x) [X, Y, Z] = meshgrid(x, y, z) Описание: Функция [X, Y] = meshgrid(x, y) формирует массивы X и Y, которые определяют координаты узлов прямоугольника, задаваемого векторами x и y. Этот прямоугольник задает область определения функции от двух переменных, которую можно построить в виде 3D-поверхности. Функция [X, Y] = meshgrid(x) является сокращенной формой записи функции [X, Y] = meshgrid(x, x). Функция [X, Y, Z] = meshgrid(x, y, z) формирует массивы X, Y и Z, которые определяют координаты узлов параллелепипеда, задаваемого векторами x, y и z. Этот параллелепипед задает область определения для вычисления функции от трех переменных и построения 3D-параметрических поверхностей. |
3.4. Команда MatLab fminbnd.
Минимизация ограниченной нелинейной функции с одной переменной.
X = fminbnd (FUN, x1, x2) пытается найти локальный минимизатор X функции.
FUN в интервале x1 <X <x2. FUN - это дескриптор функции. FUN принимает скалярный вход X и возвращает значение скалярной функции F, оцениваемое на X.
X = fminbnd (FUN, x1, x2, OPTIONS) минимизируется с помощью оптимизации по умолчанию параметры заменены значениями в структуре OPTIONS, созданной с помощью функции OPTIMSET. fminbnd использует 
эти опции: Display, TolX, MaxFunEval, MaxIter, FunValCheck, PlotFcns и OutputFcn.
X = fminbnd (ПРОБЛЕМА) находит минимум для ПРОБЛЕМЫ. ПРОБЛЕМА структуры с функцией FUN в PROBLEM.objective, интервал в PROBLEM.x1 и PROBLEM.x2, структура опций в PROBLEM.options, и имя пользователя 'fminbnd' в PROBLEM.solver.
[X, FVAL] = fminbnd (...) также возвращает значение целевой функции,
FVAL, вычисленный в FUN, в X.
[X, FVAL, EXITFLAG] = fminbnd (...) также возвращает EXITFLAG, который описывает условие выхода fminbnd. Возможные значения EXITFLAG и соответствующие условия выхода 1 fminbnd сходится с решением X на основе OPTIONS.TolX.
0 Максимальное количество оценок функций или итераций.
-1 Алгоритм завершается выходной функцией.
-2 Границы несогласованы (то есть ax> bx).
[X, FVAL, EXITFLAG, OUTPUT] = fminbnd (...) также возвращает структуру OUTPUT с количеством итераций, выполненных в OUTPUT.iterations, количество оценок функций в OUTPUT.funcCount, имя алгоритма в OUTPUT.algorithm и сообщение выхода в OUTPUT.message.
3.5. Команда MatLab abs:
Y = abs(X)
Описание:
Для массива действительных чисел X функция Y = abs(X) возвращает массив Y абсолютных значений элементов X.
Для массива комплексных чисел Z функция Y = abs(Z) возвращает массив Y модулей комплексных элементов Z.
Для строковой переменной S функция Y = abs(S) возвращает вместо символов, включая пробелы, их ASCII-коды.
4 Решение поставленных задач оптимизации
4.1 Задание 1. Сканирование функции 2-х переменных и построение поверхности равного уровня. f(x)=4x21+3x22-4x1x2+x1
Алгоритм решения.
1) Выбираем произвольный интервал для данной функции.
2) Вычисляем значение функции на данном интервале с некоторым шагом.
3) По полученным значениям определяем точку минимума заданной функции.
4) Строим график функции 2-х переменных в 3-х мерном пространстве.
5) Строим поверхность равного уровня.
6) Реализация в программной среде MatLab.
Решение.
1) Для функции f(x)=4x21+3x22-4x1x2+x1 выбрал интервал по х1 от -1 до 1 и по х2 от -1 до 1.
2) Вычислил значение функции f(x)=4x21+3x22-4x1x2+x1 на интервале от -1 до 1 с шагом 0,1. Получил таблицу значений (таблица 2).
Таблица 2
| f(x1, x2) | x1 | |||||||||||||||||||||||
| -1 | -0.9 | -0.8 | -0.7 | -0.6 | -0.5 | -0.4 | -0.3 | -0.2 | -0.1 | |||||||||||||||
| х2 | -1 | 2.0 | 1.74 | 1.56 | 1.74 | 1.44 | 1.5 | 1.64 | 1.86 | 2.16 | 2.54 | 3.00 | ||||||||||||
| -0.9 | 1.83 | 1.53 | 1.31 | 1.53 | 1.11 | 1.13 | 1.23 | 1.41 | 1.67 | 2.01 | 2.43 | |||||||||||||
| -0.8 | 1.72 | 1.38 | 1.12 | 1.38 | 0.84 | 0.82 | 0.88 | 1.02 | 1.24 | 1.54 | 1.92 | |||||||||||||
| -0.7 | 1.67 | 1.29 | 0.99 | 1.29 | 0.63 | 0.57 | 0.59 | 0.69 | 0.87 | 1.13 | 1.47 | |||||||||||||
| -0.6 | 1.68 | 1.26 | 0.92 | 1.26 | 0.48 | 0.38 | 0.36 | 0.42 | 0.56 | 0.78 | 1.08 | |||||||||||||
| -0.5 | 1.75 | 1.29 | 0.91 | 1.29 | 0.39 | 0.25 | 0.19 | 0.21 | 0.31 | 0.49 | 0.75 | |||||||||||||
| -0.4 | 1.88 | 1.38 | 0.96 | 1.38 | 0.36 | 0.18 | 0.08 | 0.06 | 0.12 | 0.26 | 0.48 | |||||||||||||
| -0.3 | 2.07 | 1.53 | 1.07 | 1.53 | 0.39 | 0.17 | 0.03 | -0.03 | -0.01 | 0.09 | 0.27 | |||||||||||||
| -0.2 | 2.32 | 1.74 | 1.24 | 1.74 | 0.48 | 0.22 | 0.04 | -0.06 | -0.08 | -0.02 | 0.12 | |||||||||||||
| -0.1 | 2.63 | 2.01 | 1.47 | 2.01 | 0.63 | 0.33 | 0.11 | -0.03 | -0.09 | -0.07 | 0.03 | |||||||||||||
| 3.0 | 2.34 | 1.76 | 2.34 | 0.84 | 0.5 | 0.24 | 0.06 | -0.04 | -0.06 | 0.00 | ||||||||||||||
| 0.1 | 3.43 | 2.73 | 2.11 | 2.73 | 1.11 | 0.73 | 0.43 | 0.21 | 0.07 | 0.01 | 0.03 | |||||||||||||
| 0.2 | 3.92 | 3.18 | 2.52 | 3.18 | 1.44 | 1.02 | 0.68 | 0.42 | 0.24 | 0.14 | 0.12 | |||||||||||||
| f(x1, x2) | x1 | |||||||||||||||||||||||
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |||||||||||||||
| х2 | 0.3 | 4.47 | 3.69 | 2.99 | 3.69 | 1.83 | 1.37 | 0.99 | 0.69 | 0.47 | 0.33 | |||||||||||||
| 0. | 5.08 | 4.26 | 3.52 | 4.26 | 2.28 | 1.78 | 1.36 | 1.02 | 0.76 | 0.58 | ||||||||||||||
| 0.5 | 5.75 | 4.89 | 4.11 | 4.89 | 2.79 | 2.25 | 1.79 | 1.41 | 1.11 | 0.89 | ||||||||||||||
| 0.6 | 6.48 | 5.58 | 4.76 | 5.58 | 3.36 | 2.78 | 2.28 | 1.86 | 1.52 | 1.26 | ||||||||||||||
| 0.7 | 7.27 | 6.33 | 5.47 | 6.33 | 3.99 | 3.37 | 2.83 | 2.37 | 1.99 | 1.69 | ||||||||||||||
| 0.8 | 8.12 | 7.14 | 6.24 | 7.14 | 4.68 | 4.02 | 3.44 | 2.94 | 2.52 | 2.18 | ||||||||||||||
| 0.9 | 9.03 | 8.01 | 7.07 | 8.01 | 5.43 | 4.73 | 4.11 | 3.57 | 3.11 | 2.73 | ||||||||||||||
| -1 | 3.54 | 4.16 | 4.86 | 5.64 | 6.50 | 7.44 | 8.46 | 9.56 | 10.74 | 12.00 | ||||||||||||||
| -0.9 | 2.93 | 3.51 | 4.17 | 4.91 | 5.73 | 6.63 | 7.61 | 8.67 | 9.81 | 11.03 | ||||||||||||||
| -0.8 | 2.38 | 2.92 | 3.54 | 4.24 | 5.02 | 5.88 | 6.82 | 7.84 | 8.94 | 10.12 | ||||||||||||||
| -0.7 | 1.89 | 2.39 | 2.97 | 3.63 | 4.37 | 5.19 | 6.09 | 7.07 | 8.13 | 9.27 | ||||||||||||||
| -0.6 | 1.46 | 1.92 | 2.46 | 3.08 | 3.78 | 4.56 | 5.42 | 6.36 | 7.38 | 8.48 | ||||||||||||||
| -0.5 | 1.09 | 1.51 | 2.01 | 2.59 | 3.25 | 3.99 | 4.81 | 5.71 | 6.69 | 7.75 | ||||||||||||||
| -0.4 | 0.78 | 1.16 | 1.62 | 2.16 | 2.78 | 3.48 | 4.26 | 5.12 | 6.06 | 7.08 | ||||||||||||||
| -0.3 | 0.53 | 0.87 | 1.29 | 1.79 | 2.37 | 3.03 | 3.77 | 4.59 | 5.49 | 6.47 | ||||||||||||||
| -0.2 | 0.34 | 0.64 | 1.02 | 1.48 | 2.02 | 2.64 | 3.34 | 4.12 | 4.98 | 5.92 | ||||||||||||||
| -0.1 | 0.21 | 0.47 | 0.81 | 1.23 | 1.73 | 2.31 | 2.97 | 3.71 | 4.53 | 5.43 | ||||||||||||||
| 0.14 | 0.36 | 0.66 | 1.04 | 1.50 | 2.04 | 2.66 | 3.36 | 4.14 | 5.00 | |||||||||||||||
| 0.1 | 0.13 | 0.31 | 0.57 | 0.91 | 1.33 | 1.83 | 2.41 | 3.07 | 3.81 | 4.63 | ||||||||||||||
| 0.2 | 0.18 | 0.32 | 0.54 | 0.84 | 1.22 | 1.68 | 2.22 | 2.84 | 3.54 | 4.32 | ||||||||||||||
| 0.3 | 0.29 | 0.39 | 0.57 | 0.83 | 1.17 | 1.59 | 2.09 | 2.67 | 3.33 | 4.07 | ||||||||||||||
| 0. | 0.46 | 0.52 | 0.66 | 0.88 | 1.18 | 1.56 | 2.02 | 2.56 | 3.18 | 3.88 | ||||||||||||||
| 0.5 | 0.69 | 0.71 | 0.81 | 0.99 | 1.25 | 1.59 | 2.01 | 2.51 | 3.09 | 3.75 | ||||||||||||||
| 0.6 | 0.98 | 0.96 | 1.02 | 1.16 | 1.38 | 1.68 | 2.06 | 2.52 | 3.06 | 3.68 | ||||||||||||||
| 0.7 | 1.33 | 1.27 | 1.29 | 1.39 | 1.57 | 1.83 | 2.17 | 2.59 | 3.09 | 3.67 | ||||||||||||||
| 0.8 | 1.74 | 1.64 | 1.62 | 1.68 | 1.82 | 2.04 | 2.34 | 2.72 | 3.18 | 3.72 | ||||||||||||||
| 0.9 | 2.21 | 2.07 | 2.01 | 2.03 | 2.13 | 2.31 | 2.57 | 2.91 | 3.33 | 3.83 | ||||||||||||||
| 2.74 | 2.56 | 2.46 | 2.44 | 2.5 | 2.64 | 2.86 | 3.16 | 3.54 | 4.00 | |||||||||||||||
3)По полученным значениям определил точку минимума функции f(x)=4x21+3x22-4x1x2+x1. Минимум функции при х1=0 и х2=0 равен нулю.
4) Построил график функции f(x)=4x21+3x22-4x1x2+x1 с помощью команды MatLab plot3(х1,х2,f).
Результат построения графика представлен на рисунке 1.
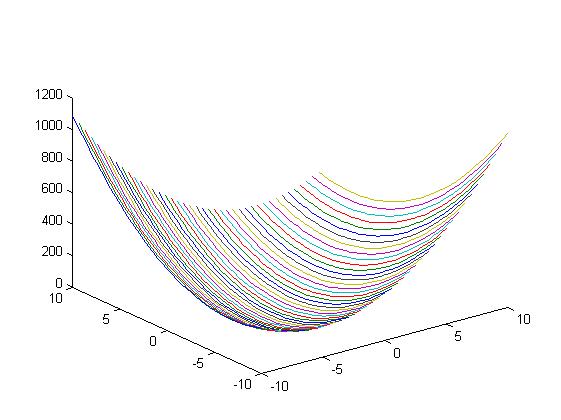
Рисунок 1График функции f(x)=4x21+3x22-4x1x2+x1
5) Построил поверхность равного уровня функции f(x)=4x21+3x22-4x1x2+x1 с помощью команды MatLab contour(x1,x2,f).
Результат построения поверхности уровня представлен на рисунке 2
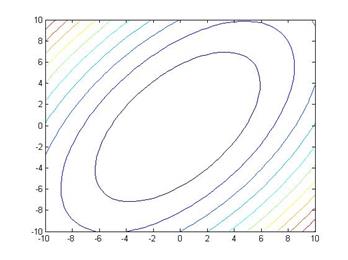
Рисунок 2 Поверхность равного уровня функции f(x)=4x21+3x22-4x1x2+x1
6) Реализовал в программной среде MatLab.
Код программы:
Задаем массив данных х1:
x1=-10:0.5:10
Задаем массив данных х2:
x2=-10:0.5:10
Формируем узлы двухмерной сетки:
[x1,x2]=meshgrid(x1,x2)
Записываем исходную функцию на языке MatLab:
f=4*x1.^2+3*x2.^2-4*x1.*x2+x1
Строим график исходной функции:
plot3(x1,x2,f)
figure
Строим поверхность равного уровня:
contour(x1,x2,f)
4.2 Задание 2. Задача одномерной безусловной оптимизации
Метод сканирования функции 1-ой переменой. Алгоритм решения.
1) Методом Свенна выбираем интервал для данной функции.
2) Вычисляем значение функции на данном интервале с некоторым шагом.
3) По полученным значениям определяем точку минимума заданной функции.
4) Строим график функции 1-ой переменной.
5) Реализация в программной среде MatLab.
1) Для функции f(x)=x2+6x+12 выбрал интервал по х от -5 до 5.
2) Вычислил значение функции f(x)=x2+6x+12 на интервале от -5 до 5 с интервалом 0,5. Получил таблицу значений (таблица3):
Таблица 3
| Х | f(x) |
| -5 | 7.0 |
| -4,5 | 5.25 |
| -4 | |
| -3,5 | 3.25 |
| -3 | |
| -2,5 | 3.25 |
| -2 | |
| -1,5 | 5.25 |
| -1 | |
| -0,5 | 9.25 |
| 0,5 | 15.25 |
| 19.0 | |
| 1,5 | 23.25 |
| Х | f(x) |
| 2,5 | 33.25 |
| 3,5 | 45.25 |
| 4,5 | 59.25 |
| 67.0 |
По данным таблицы построил график 1
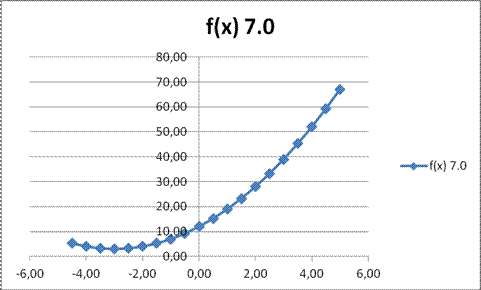
График 1. Значение функции f(x)=x2+6x+12
По полученным данным видно, что минимум находится на отрезке [-3.5:-2.5]. Просканируем данный интервал с шагом 0.2. (Таблица 4)
Таблица 4
| Х | f(x) |
| -3.5 | 3.25 |
| -3.3 | 3.09 |
| -3.1 | 3.01 |
 -2.9
| 3.01 |
| -2.7 | 3.09 |
| -2.5 | 3.25 |
По таблице 4 построил график 1.
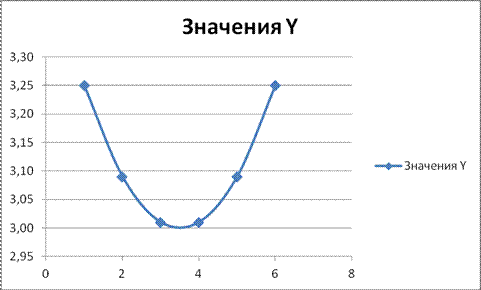
Гафик 1. Значение функции f(x)=x2+6x+12 при х=[-3,5:-2,5]
По полученным данным видно, что минимум находится на отрезке [-3.1:-2.9]. Просканируем данный интервал с шагом 0.05.
Получил таблицу 5.
Таблица 5
| Х | f(x) |
| -3.1 | 3.01 |
| -3.05 | 3.0025 |
| -3 | |
| -2.95 | 3.0025 |
| -2.9 | 3.01 |
По таблице 5 построил график 2.
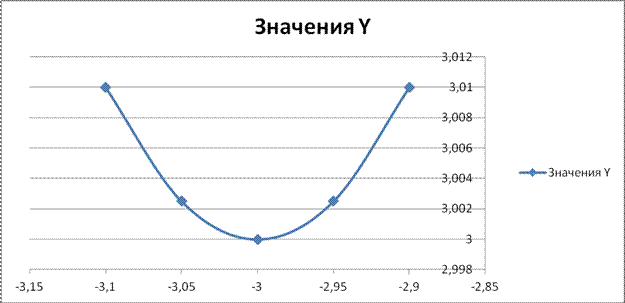
График 2. График функции f(x)=x2+6x+12 при х=[-3,1:-2,95]
По вычисленным значениям функции видно, что минимум её находится в точке Х=-3 и равен f(x)=3.
3) По полученным значениям определил точку минимума функции f(x)=x2+6x+12. Минимум функции равный 3, получается при х=-3.
4) Построил график функции f(x)=x2+6x+12.Результат представлен на графике 3.
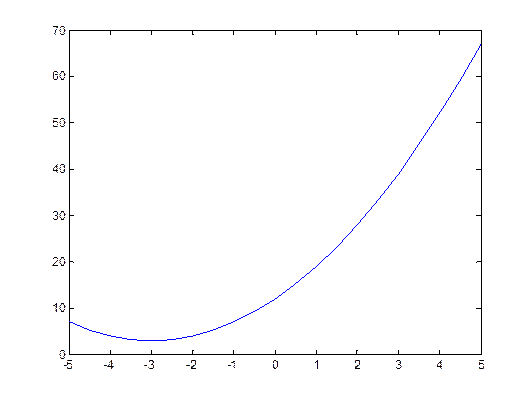
График 3. График функции f(x)=x2+6x+12 при х=[-3,1:-2,95]
5) Реализовал в программной среде MatLab.
Задал массив данных по х:
x=[-5:0.5:5]
Записал исходную функцию на языке MatLab:
f=x.^2+6*x+12
Построил график функции:
plot(x,f)
Находим минимум функции по найденным точкам:
[M,N]=min(f)
x(N)
Минимизируем ограниченную нелинейную функцию одной переменной:
[x,y,flag,out]=fminbnd(@f1,-5,5)
Создаю второй файл с функцией:
function f1=f1(x)
f1 = x.^2+6*x+12;
4.3 Задание 3 Задача безусловной одномерной и многомерной оптимизации
Метод дихотомии
Постановка задачи
Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку x*єR, f(x*)= min f(x).
х є R
Стратегия поиска
Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. Для их нахождения текущий интервал неопределенности делится пополам и в обе стороны от середины откладывается по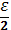 
, где ε– малое положительное число. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм.
Шаг 1. Задать начальный интервал неопределённости L0=[a0,b0], ε - малое число, l>0 точность.
Шаг 2. Положить k=0.
Шаг 3. Вычислить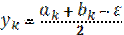 
, f(yk), 
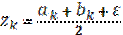, f(zk)
Шаг 4. Сравнить f(yk), с f(zk):
а) если f(yk)≤f(zk), положить ak+1=ak, bk+1=bk и перейти к шагу 5
б) если f(yk)>f(zk), положить ak+1=yk, bk+1=bk.
Шаг 5. Вычислить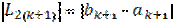 
и проверить условия окончания:
а) если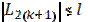 
, процесс поиска завершается и 
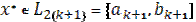. В качестве приближенного решения можно взять середину последнего интервала:
;
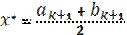б) если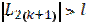 
, положить k=k+1 и перейти к шагу 3.
Сходимость
Для метода дихотомии характеристика относительного уменьшения начального интервала неопределенности находится по формуле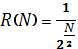 
, где N–количество вычислений функции.
Решение задачи аналитически:
x=[0,1:1]
ℇ=0,05
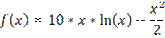
1 итерация
Начальный интервал [0,1:1]
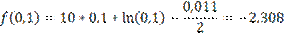
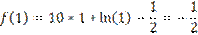
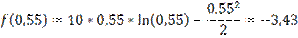
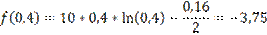
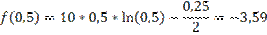
f(0,4)<f(0,5) => новый интервал [0,1:0,5]
2 итерация
Начальный интервал [0,1:0,5]
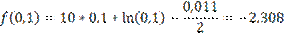
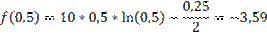
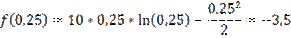
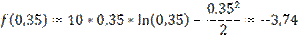
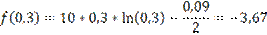
f(0,25)>f(0,35) => новый интервал [0,25:0,5]
3 итерация
Начальный интервал [0,25:0,5]
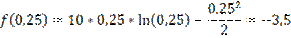
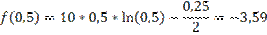
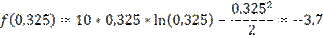
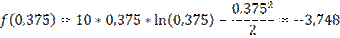
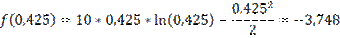
f(0,325)<f(0,425) => новый интервал [0,325:0,5]
Реализация в программной среде Matlab.
% Шаг1
Задаем начальный интервал неопределенности L0:
L0=[0.1;1]
Задаем точность, с которой будет производиться вычисление:
E=0.1
Задаем начальное значение для l:
l=1
% Шаг2
Задаем начальное значение для k:
k=0
% Шаг3
Задаем начальное зачение a0=0.1, b0=1
a0=0.1
b0=1
Вычисляем функции y0 и z0:
y0=(a0+b0-E)/2
f1=10*y0*log(y0)-y0.^2/2
z0=(a0+b0+E)/2
f2=10*z0*log(z0)-z0.^2/2
Сравниваем f1 и f2 и определяем начальные значения a1 и b1:
% Шаг4
if f1<f2
a1=a0
b1=z0
else
a1=y0
b1=b0
end
% Шаг5
Задаем интервал L1:
L1=abs(b1-a1)
Проверка условий окончания поиска:
if L1<=l
% Решение найдено
x1=a1
x2=b1
L2=[y0;z0]
x=(a1+b1)/2
f=10*x*log(x)-x.^2/2
else
y1=(a1+b1-E)/2
f1=10*y1*log(y1)-y1.^2/2
z1=(a1+b1+E)/2
f2=10*z1*log(z1)-z1.^2/2
end
Строим график функции:
[x,y,flag,out]=fminbnd(@zador,0.1,1)
ВЫВОД
В результате выполнения курсовой работы был разработан алгоритм решения поставленных задач, написаны программы метода сканирования и метод