Аппроксимация функций с помощью метода
Наименьших квадратов
Метод наименьших квадратов применяется при обработке результатов эксперимента для аппроксимации (приближения) экспериментальных данных аналитической формулой. Конкретный вид формулы выбирается, как правило, из физических соображений. Такими формулами могут быть:



и другие.
Сущность метода наименьших квадратов состоит в следующем. Пусть результаты измерений представлены таблицей:
| Таблица | ||||
| x | x1 | x2 | … | xn |
| y | y1 | y2 | … | yn |
Будем считать, что вид аппроксимирующей (приближающей) зависимости выбран, и её можно записать в виде
| (1) | |

|
где f - известная функция, a0, a1, …, am - неизвестные постоянные параметры, значения которых надо найти. В методе наименьших квадратов приближение функции (1) к экспериментальной зависимости считается наилучшим, если выполняется условие

|
то есть суммa квадратов отклонений искомой аналитической функции от экспериментальной зависимости должна быть минимальна.
Заметим, что функция Q называется невязкой.

Так как невязка

то она имеет минимум. Необходимым условием минимума функции нескольких переменных является равенство нулю всех частных производных этой функции по параметрам. Таким образом, отыскание наилучших значений параметров аппроксимирующей функции (1), то есть таких их значений, при которых Q = Q(a0, a1, …, am) минимальна, сводится к решению системы уравнений:
.
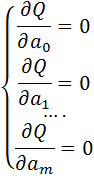
| (4) |
Методу наименьших квадратов можно дать следующее геометрическое истолкование: среди бесконечного семейства линий данного вида отыскивается одна линия, для которой сумма квадратов разностей ординат экспериментальных точек и соответствующих им ординат точек, найденных по уравнению этой линии, будет наименьшей.
Нахождение параметров линейной функции
Пусть экспериментальные данные надо представить линейной функцией:

|
Требуется подобрать такие значения a и b, для которых функция

| (5) |
будет минимальной. Необходимые условия минимума функции (4) сводятся к системе уравнений:

После преобразований получаем систему двух линейных уравнений с двумя неизвестными:
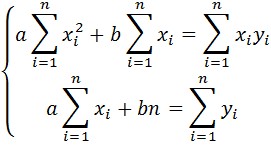
| (6) |
решая которую, находим искомые значения параметров a и b.
Нахождение параметров квадратичной функции
Если аппроксимирующей функцией является квадратичная зависимость

|
то её параметры a, b, c находят из условия минимума функции:

| (7) |
Условия минимума функции (7) сводятся к системе уравнений:

|
После преобразований получаем систему трёх линейных уравнений с тремя неизвестными:

|
при решении, которой находим искомые значения параметров a, b и c.
Пример. Пусть в результате эксперимента получена следующая таблица значений x и y:
| Таблица 5 | ||||||||
| xi | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 |
| yi | 0,705 | 0,495 | 0,426 | 0,357 | 0,368 | 0,406 | 0,549 | 0,768 |
Требуется аппроксимировать экспериментальные данные линейной функцией.
Таблица
| N | xi | 
| 
| 
|
| 0,5 | 0,25 | 0,705 | 0,3225 | |
| 0,6 | 0,36 | 0,495 | 0,2970 | |
| 0,7 | 0,49 | 0,426 | 0,2982 | |
| 0,8 | 0,64 | 0,357 | 0,2856 | |
| 0,9 | 0,81 | 0,368 | 0,3312 | |
| 1,0 | 1,0 | 0,406 | 0,4060 | |
| 1,1 | 1,21 | 0,549 | 0,6039 | |
| 1,2 | 1,44 | 0,768 | 0,9216 | |
| Σ | 6,8 | 6,2 | 4,074 | 3,496 |
Подставляя вычисленные суммы в систему (6) получаем линейную систему с двумя неизвестными:
6,2a + 6,8b = 3,496
6,8a + 8b = 4,074
Отсюда: a = 0,07365; b = 0,4469
Следовательно, вид полинома: y = 0,07365 + 0,4469
Вид полинома показан на графике.

В системе MathCad это делается так:

Зависимость:
y = 0,079x + 0,442
Более точная аппорксимация с помощью квадратичной функции

Зависимость:

вектор разности
между текущим и
начальным моментами
наблюдений
вектор значений блеска
переменной



вид искомой функции





коэффициенты вектора F
Рис.1 Последовательность вычислений
Звёздные величины

Разность между текущим и начальным моментами наблюдений
Рис.2. Искомая усреднённая кривая изменения блеска переменной (пунктир) и наблюдательные точки (крестики)
Обработка результатов наблюдений мирид с помощью универсальной математической системы MathCad.
Известно, что глазомерные оценки блеска переменных звёзд, особенно любительские, не отличаются большой точностью. Опытные переменщики знают как сильно влияют на точность оценок время суток, подсветка, атмосферные условия и другие факторы, в том числе и физическое состояние наблюдателя. Следовательно, возможность точного определения максимума или минимума блеска представляется сомнительной, если не пользоваться статистическими методами обработки результатов наблюдений. Профессионалы используют для этого свои оригинальные программные продукты, которые в большинстве случаев любителям недоступны. Поэтому Автор советует использовать для статистической обработки глазомерных оценок блеска широко распространённую систему MathCad (см. например MathCad 6.0 PLUS, Изд. Филинъ, 1997 или Дьяконов В.П., Абраменкова И.В. MathCad 7, М.: “Нолидж”, 1998). Эта система имеет большой выбор статистических операторов.
В качестве примера Автором получено уточнённое значение максимума блеска мириды U Ori. Определение максимума сводится к аппроксимации совокупности наблюдательных точек, если рассматривать их как проявления некоторого случайного процесса. Особенно удобно это делать, если таких точек недостаточно, например несколько оценок имеется на восходящем участке кривой блеска, несколько – на нисходящем. Момент максимума неизвестен, поэтому плавная аппроксимирующая кривая поможет уточнить его момент, даже при отсутствии наблюдений в это время. Плавная кривая проводится через наблюдательные точки не “на глазок” как это предлагается в известной книге В.П.Цесевича “Переменные звёзды и их наблюдение” (1980) или в книге “Переменные звёзды” (К.Гоффмейстер, Г.Рихтер, В.Венцель, 1989), а с использованием MathCad”овского оператора linfit, принцип работы которого основан на методе наименьших квадратов.
Вначале задаём вектор vx – совокупность моментов наблюдений. Для удобства каждое число – разность значений JDi – JD0, где JDi - момент наблюдений, а JD0 – некоторый выбранный момент близкий к начальному. Затем задаётся вектор vy - совокупность звёздных величин. Таким образом получено два вектора, в которых каждому моменту наблюдений поставлена в соответствие оценка блеска. Затем необходимо подобрать вид искомой функции приближения. Казалось бы, если речь идёт о периодических переменных, такая функция также должна быть периодической, например синусоидальной, но любитель, как правило, имеет возможность наблюдать мириды в состоянии близком к максимуму, к тому же не забудем, что у мирид часто изменяется период и форма кривой блеска, поэтому аппроксимация периодической функцией может оказаться неэффективной. Кроме того, интерес представляют как раз моменты максимумов мирид, что с ними делается в другое время не столь важно. Поэтому лучше всего искать приближение в виде функции, имеющей, по меньшей мере, один ярко выраженный экстремум, но несимметричной, так как подъём блеска у мирид происходит быстрее, чем его падение, что, кстати, видно из совокупности полученных моментов наблюдений(рис.2). Таким образом, наилучшей функцией для аппроксимации представляется степенная, но не выше третьего порядка. Можно показать, что дальнейшее уточнение приводит к появлениям бесконечно малых высшего порядка и не представляет интереса (это чисто математическое доказательство приводить здесь нецелесообразно). На рис.1 показана последовательность вычислений с необходимыми комментариями, являющаяся весьма простой даже для школьника или студента младшего курса.
Единственная сложность заключается, пожалуй, в подборе аппроксимирующей функции, который основывается на интуиции исследователя, но пытливого человека такие трудности должны не пугать, а, напротив, вдохновлять. Эта зависимость показана на рис.2 в виде пунктирной кривой. Крестиками показаны наблюдательные точки. Итак полученная нами плавная кривая описывается многочленом третьей степени. Его коэффициенты показаны на рис.1 в виде вектора F(x). Последовательность дальнейших действий такова. Этот многочлен необходимо продифференцировать и производную приравнять нулю. Таким образом получится уравнение второй степени с одним неизвестным. Теперь, если ненулевое решение этого уравнения прибавим к JD0 (см. выше) получим точное значение момента максимума в Юлианских днях. Как видно из рис.2 усреднённый момент максимума не совпадает с моментом наблюдений максимального блеска, но именно он является более близким к истинному, так как статистическая обработка, если не исключает полностью, то в наибольшей степени снижает влияние ошибок, основные причины которых перечислены выше. В данном случае исследование полученной усреднённой кривой на экстремум даёт значение максимума блеска мириды M = 2451512.5JD. Соответствующий этому значению визуальный блеск mvis = 7m.37.
Вычислительную систему MathCad рекомендуем применять лишь для статистического анализа, последовательность действий которого приведена на рис.1. Дальнейший процесс исследования аппроксимирующей функции на максимум должен быть хорошо знаком всякому школьнику 10-11 класса, поэтому применение мощных средств вычислительной техники для таких элементарных операций нецелесообразно. Кроме того, важно, что в этом случае начинающему любителю – школьнику или студенту предоставляется возможность применить на практике, полученные в школе знания, и, используя абстрактную математику получить пусть не очень значительный, но реальный научный результат.

|

|

|

|

|

|
Функция: 
Производная функции:
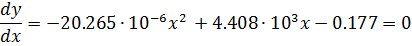
Отсюда x = 53.164 подставляем в исходное уравнение и получаем близкое к истинному значение измеряемой величины – блеск звезды:

