Одним из важных показателей имущественного страхования является уровень убыточности страховых сумм (q), представляющий собой долю выплат страхового возмещения (W) в страховой сумме застрахованного имущества (S):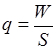 
Уровень убыточности страховых сумм по совокупности объектов определяется по формуле,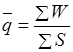 
, или 
,
где 
- средняя сумма страхового возмещения 
.
Средняя страховая сумма застрахованных объектов: 
,
где N - общее количество застрахованных объектов;
п - число пострадавших объектов.
Если 
, то 
Отношение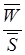 
- называется коэффициентом тяжести страховых событий (Кm) следовательно, 
.
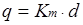Таким образом, уровень убыточности страховых сумм зависит от тяжести страховых событий и доли пострадавших объектов.
Динамику убыточности страховых сумм можно охарактеризовать системой индексов: 
, или 
Используя индексный метод, можно определить абсолютный прирост (снижение), уровень убыточности страховых сумм, обусловленный изменением уровня тяжести страховых событий и доли пострадавших объектов: 
Изменение абсолютного прироста страховых сумм происходит за счет:
а) уменьшения тяжести страховых событий 
б) изменения доли пострадавших объектов 
Динамику среднего уровня убыточности изучает система индексов переменного и постоянного состава, структурных сдвигов: индекс средней убыточности переменного состава 
,
индекс средней убыточности постоянного состава 
,
индекс структурных сдвигов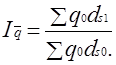 
.
Представим взаимосвязь индексов убыточности переменного, постоянного составов и структурных сдвигов: 
На основе этих индексов рассчитываются абсолютные изменения средней убыточности: 
Изменение средней убыточности выявляется по факторам:
а) за счет изменения убыточности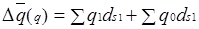 
б) за счет структурных сдвигов 
Одной из задач статистики страхования является обоснование уровня тарифной ставки. От того, насколько объективно обоснована тарифная ставка, зависит финансовое состояние страховых органов, уровень развития страхового дела, взаимоотношения со страхователями.
Тарифная ставка предназначена для возмещения ущерба, причиненного страховому имуществу стихийными бедствиями и другими страховыми событиями. Она состоит из двух частей: нетто-ставки и нагрузки (надбавки). Нетто-ставка составляет основную часть тарифа и предназначена для создания фонда на выплату страхового возмещения. Надбавка служит для образования резервных фондов.
Нетто-ставка рассчитывается с определенной степенью вероятности по формуле 
,
где 
- средний уровень убыточности за период;
t - коэффициент доверительной вероятности, определяемой по таблице на основании заданной вероятности;
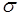- среднее квадратическое отклонение индивидуальных уровней убыточности от среднего уровня. 
Брутто-ставка состоит из нетто-ставки и надбавки и рассчитывается по формуле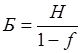 
,
где f - доля нагрузки по страхованию имущества в брутто-ставке.
В имущественном страховании проводят оценку устойчивости страхового дела с помощью показателя - коэффициента финансовой устойчивости: 
,
где 
- дисперсия признака.
Расчетная часть
Вариант №20
Имеются следующие выборочные данные о деятельности страховых организаций одного из регионов в отчётном году (выборка 10%- ная, механическая), млн. руб.:
Таблица2.1
Выборочные данные о деятельности страховых организаций (исходные данные)
| № организации, п/п | Доходы | Прибыль | № организации, п/п | Доходы | Прибыль |
| 9,7 | 0,41 | 8,0 | 0,40 | ||
| 9,0 | 0,40 | 12,2 | 0,58 | ||
| 10,2 | 0,45 | 13,5 | 0,63 | ||
| 10,3 | 0,46 | 13,9 | 0,65 | ||
| 9,8 | 0,42 | 10,5 | 0,49 | ||
| 10,0 | 0,44 | 10,7 | 0,50 | ||
| 6,0 | 0,25 | 10,8 | 0,50 | ||
| 10,5 | 0,48 | 8,5 | 0,34 | ||
| 16,0 | 0,75 | 8,5 | 0,35 | ||
| 11,6 | 0,53 | 12,2 | 0,58 | ||
| 11,7 | 0,54 | 11,5 | 0,52 | ||
| 12,8 | 0,56 | 13,3 | 0,60 | ||
| 11,9 | 0,55 | 13,8 | 0,64 | ||
| 8,5 | 0,38 | 15,0 | 0,70 | ||
| 7,0 | 0,31 | 13,5 | 0,64 |
Задание №1
По исходным данным:
1. Постройте статистический ряд распределения предприятий по признаку – доходы страховых организаций, образовав, пять групп с равными интервалами.
2. Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
Сделайте выводы по результатам выполнения задания.
Для того чтобы произвести группировку необходимо вычислить величину группировочного интервала по формуле:
i = 
, где
- соответственно максимальное и минимальное значение доходов страховых организаций, где 
- число образуемых групп.
i =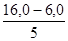 
=2 млн. руб.
Образуем группы которые отличаются друг от друга по доходам на величину интервала:
I 6,0 – 8,0 млн. руб.
II 8,0 – 10,0 млн. руб.
III 10,0 – 12,0 млн. руб.
IV 12,0 – 14,0 млн. руб.
V 14,0 – 16,0 млн. руб.
Группировку представим в рабочей таблице 2.2.
Таблица 2.2.
Группировка страховых организаций по размеру денежных доходов.
| Группы | Группы страховых организаций по доходам, млн. руб. | Номер организации | Доходы, млн. руб. |
| 6,0 | |||
| I | 6,0-8,0 | 7,0 | |
| 8,0 | |||
| Итого | |||
| 9,7 | |||
| 9,0 | |||
| II | 8,0-10,0 | 9,8 | |
| 10,0 | |||
| 8,5 | |||
| 8,5 | |||
| 8,5 | |||
| Итого | |||
| 10,2 | |||
| 10,3 | |||
| III | 10,0-12,0 | 10,5 | |
| 11,6 | |||
| 11,7 | |||
| 11,9 | |||
| 10,5 | |||
| 10,7 | |||
| 10,8 | |||
| 11,5 | |||
| Итого | |||
| 12,8 | |||
| 12,2 | |||
| 13,5 | |||
| IV | 12,0-14,0 | 13,9 | |
| 12,2 | |||
| 13,3 | |||
| 13,8 | |||
| 13,5 | |||
| Итого | |||
| V | 14,0-16,0 | 16,0 | |
| 15,0 | |||
| Итого |
В результате группировке получили следующий ряд распределения (таблица 2.3.):
Таблица 2.3.
Распределение страховых организаций по доходам
| Группы | Группы организаций по доходам страховых организаций, млн. руб. | Число организаций |
| I | 6,0-8,0 8,0-10,0 | |
| II | ||
| III | 10,0-12,0 | |
| IV | 12,0-14,0 | |
| V | 14,0-16,0 |
Расчёт характеристик произведем в рабочей таблице (таблица 2.4.)
Таблица 2.4.
Расчёт характеристик ряда распределения.
| Группы | Группы организаций по доходам, млн. руб. | Число организа-ций (f) | 
| 
| 
| 
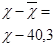
| ƒнак. |
| I | 6,0-8,0 | -3,933 | 46,405 | ||||
| II | 8,0-10,0 | -1,933 | 26,155 | ||||
| III | 10,0-12,0 | 0,067 | 0,045 | ||||
| IV | 12,0-14,0 | 2,067 | 34,18 | ||||
| V | 14,0-16,0 | 4,067 | 33,081 | ||||
| Итого | 139,866 |
Среднее арифметическое находим по формуле средне арифметическая взвешенная: 
, где
- сумма произведений величины признаков на их частоту;
- общая численность единиц совокупности.
= 
млн. руб.
Дисперсию вычислим по формуле:
= 
Среднее квадратическое отклонение определим по формуле:
млн. руб.
Коэффициент вариации найдем по формуле:
; 
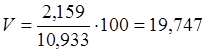=19,7%
Вывод: 19,7% < 33%, т.к. коэффициент вариации меньше 33%, то совокупность по доходам страховых организаций считается однородной.
Рассчитываем моду:
= 16 млн. руб.
Вывод: в данной совокупности наиболее часто встречаются страховые организации с доходом 16 млн. руб.
Найдём медиану:
; 
= 11,428 млн. руб.
Вывод: в данной совокупности 50% страховых организаций имеют доход более 11,428 млн. руб, а 50% страховых организаций менее.
ВЫВОД: расчеты, проведенные по ряду распределения показали, что средний доход страховых организаций изучаемой совокупности составил 10,933 млн. руб, при среднем квадратическом отклонении 2,159 млн. руб, коэффициент вариации составил 19,7% это означает, что совокупность однородна по изучаемому признаку. Наиболее часто встречаются организации с доходом 16 млн. руб, а также у 50% страховых организаций доход более 11,428 млн. руб, а у остальных 50% организаций менее.
Задание № 2.
По исходным данным:
1. Установите наличие и характер связи между признаками денежный доход и прибыль, методом аналитической группировки образовав, пять групп с равными интервалами по факторному признаку.
2. Измерьте тесноту корреляционной связи между названными признаками с использованием коэффициентов детерминации и эмпирического корреляционного отношения.
Решение:
Обоснуем выбор факторного признака: из экономической теории известно, что доход организаций высчитывают из прибыли организаций, от величины которой и зависит доход предприятия, следовательно, фактор прибыль страховых организаций должен быть взят в основу группировки.
Для того чтобы произвести группировку необходимо вычислить величину группировочного интервала по формуле:
i = , где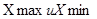 
- соответственно максимальное и минимальное значение прибыли страховых организаций, где 
- число образуемых групп. i = 
= 0,1 млн. руб.
Образуем группы которые отличаются друг от друга, по размеру прибыли организаций на эту величину интервала:
I 0,25 – 0,35 млн. руб.
II 0,35 – 0,45 млн. руб.
III 0,45 – 0,55 млн. руб.
IV 0,55 – 0,65 млн. руб.
V 0,65 – 0,75 млн. руб.
Аналитическую группировку произведем в рабочей таблице 2.5.
Таблица 2.5.
Рабочая таблица с аналитической группировкой.
| Группы | Группы страховых организаций по прибыли, млн. руб. | Номер организации | Прибыль, млн. руб. | Доход, млн. руб |
| 0,25 | 6,0 | |||
| 0,31 | 7,0 | |||
| I | 0,25-0,35 | 0,34 | 8,5 | |
| 0,35 | 8,5 | |||
| Итого | 1,25 | |||
| 0,41 | 9,7 | |||
| 0,40 | 9,0 | |||
| 0,45 | 10,2 | |||
| 0,42 | 9,8 | |||
| 0,44 | 10,0 | |||
| II | 0,35-0,45 | 0,38 | 8,5 | |
| 0,40 | 8,0 | |||
| Итого | 2,9 | 65,2 | ||
| 0,46 | 10,3 | |||
| 0,48 | 10,5 | |||
| III | 0,45-0,55 | 0,53 | 11,6 | |
| 0,54 | 11,7 | |||
| 0,55 | 11,9 | |||
| 0,49 | 10,5 | |||
| 0,50 | 10,7 | |||
| 0,50 | 10,8 | |||
| 0,52 | 11,5 | |||
| Итого | 4,57 | 99,5 | ||
| 0,56 | 12,8 | |||
| IV | 0,55-0,65 | 0,58 | 12,2 | |
| 0,63 | 13,5 | |||
| 0,65 | 13,9 | |||
| 0,58 | 12,2 | |||
| 0,60 | 13,3 | |||
| 0,64 | 13,8 | |||
| 0,64 | 13,5 | |||
| Итого | 4,88 | 105,2 | ||
| V | 0,65-0,75 | 0,75 | 16,0 | |
| 0,70 | 15,0 | |||
| Итого | 1,45 | |||
| Всего | 15,05 | 330,9 |
На основании рабочей таблицы составляем сводную итоговую аналитическую таблицу (таблица 2.6.):
Таблица 2.6.
Сводная итоговая аналитическая таблица
| Группы | Группы организаций по прибыли, млн. руб. | Число организаций | Прибыль, млн. руб. | Доход, млн.руб. | ||
| Всего по группам | На 1 организцию | Всего по группам | На 1 организа- цию | |||
| I | 0,25-0,35 | 1,25 | 0,313 | 7,5 | ||
| II | 0,35-0,45 | 2,9 | 0,414 | 65,2 | 9,314 | |
| III | 0,45-0,55 | 4,57 | 0,508 | 99,5 | 11,056 | |
| IV | 0,55-0,65 | 4,88 | 0,61 | 105,2 | 13,15 | |
| V | 0,65-0,75 | 1,45 | 0,725 | 15,5 | ||
| Итого | 15,05 | 2,57 | 330,9 | 56,52 |
Вывод: сравнивая графы 5 и 7 аналитической таблицы, мы видим, что с увеличением прибыли страховых организаций растет их доход, отсюда следует, между этими показателями имеется прямая зависимость.
Вычислим коэффициент детерминации, который представляет собой отношение межгрупповой дисперсии к общей дисперсии.
Эмпирический коэффициент детерминации найдем по формуле:
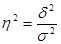, где
- межгрупповая дисперсия,
- общая дисперсия.
Расчет межгрупповой дисперсии представим в рабочей таблице 2.7:
Таблица2.7.
Рабочая таблица с расчетом межгрупповой дисперсии.
| Группы |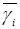 
| Число организаций (f) | 
| 
|
| I | 7,5 | -3,53 | 49,844 | |
| II | 9,314 | -1,716 | 20,615 | |
| III | 11,056 | 0,026 | 0,009 | |
| IV | 13,15 | 2,12 | 35,952 | |
| V | 15,5 | 4,47 | 39,962 | |
| Итого | 146,382 |
Межгрупповую дисперсию найдем по формуле:
Общую дисперсию рассчитаем по формуле:
,для вычисления необходимо найти среднее значение квадрата признака по формуле 
Расчет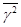 
произведем в рабочей таблице (таблица 2.8.)
Таблица 2.8.
Рабочая таблица с расчетом среднего значения квадрата признака.
| Номер организа-ции | Доход (у), млн. руб. | У2 | Номер организа-ции | Доход (у), млн. руб. | У2 |
| 9,7 | 94,09 | 8,0 | 64,0 | ||
| 9,0 | 81,0 | 12,2 | 148,84 | ||
| 10,2 | 104,04 | 13,5 | 182,25 | ||
| 10,3 | 106,9 | 13,9 | 193,21 | ||
| 9,8 | 96,04 | 10,5 | 110,25 | ||
| 10,0 | 100,0 | 10,7 | 114,49 | ||
| 6,0 | 36,0 | 10,8 | 116,64 | ||
| 10,5 | 110,25 | 8,5 | 72,25 | ||
| 16,0 | 256,0 | 8,5 | 72,25 | ||
| 11,6 | 134,56 | 12,2 | 148,84 | ||
| 11,7 | 136,89 | 11,5 | 132,25 | ||
| 12,8 | 163,84 | 13,3 | 176,89 | ||
| 11,9 | 141,61 | 13,8 | 190,44 | ||
| 8,5 | 72,25 | 15,0 | 225,0 | ||
| 7,0 | 49,0 | 13,5 | 182,25 | ||
| Итого | 3812,32 |
; 
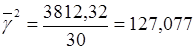
Общая дисперсия равна:
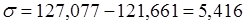
Считаем коэффициент детерминации: 
или 90,1%
Вывод: вариация дохода страховых организаций на 90,1% обусловлена вариацией прибыли и на 9,9% вариации прочих факторов.
Найдем эмпирическое корреляционное отношение по формуле:
Так как эмпирическое корреляционное отношение больше 0,7 можно сделать вывод, что связь между прибылью и доходом страховых организаций высокая.
Задание № 3.
По результатам выполнения задания 1 с вероятностью 0,954 определите:
1. Ошибку выборки средней величины доходов и границы, в которых она будет находиться в генеральной совокупности.
млн. руб.
=4,662
=30 – 10%
N=300 – 100%
, где
- численность выборочной совокупности;
- численность генеральной совокупности.
тыс. руб.
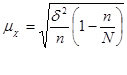
Найдем предельную ошибку:
, где
- нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки;
- средняя ошибка выборки.
= 
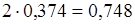тыс. руб.
(p=0,954; t=2)
Найдем границы:
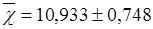
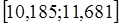
Вывод: с вероятностью 0,954 можно утверждать, что доход страховых организаций в генеральной совокупности будет находится в пределах от 10,185 млн. руб. до 11,681 млн. руб.
2.Ошибку выборки доли страховых организаций с доходами 14 млн. руб. и более и границы, в которых будет находиться генеральная доля:
; 
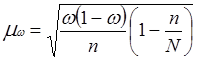
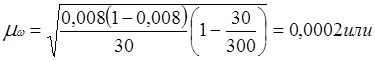0,02%
Посчитаем предельную ошибку:
; 
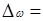2*0,0002=0,0004 или 0,04%
Найдем пределы:
Вывод: с вероятностью 0,954 можно утверждать, что ошибка в выборке доли организаций с доходом 14 млн. руб. и более составляет 0,04%, границы в которых находится генеральная доля от 0,76% до 0,84%.
Задание №4
Определите тарифную ставку страхования профессиональной ответственности аудиторов при средней убыточности 55 руб. на 100 руб. страховых сумм, экспертной оценке вероятности наступления страхового события – 0,05, числе договоров – 1200, доле абсолютной нагрузки в брутто – ставке – 25% и вероятности непревышения возмещения по сравнению со страховыми суммами – 0,997
Решение:
Определим часть нетто – ставки страхования:
и0=55*0,05=2,75руб. на 100 руб. страховой суммы.
Определяемрисковую надбавку
, где
и0 – основная часть нетто – ставки
ир – рисковая часть
э – экспертная оценка вероятности наступления страхового случая
t – коэффициент доверия, кратности не превышения возмещения по сравнению со страховыми суммами:
N – количество договоров
dF – доля абсолютной нагрузки в брутто – ставке.
руб. со 100 руб. страховой суммы.
Определим брутто – ставку (тариф) страхователя:
руб. со 100 руб. страховой суммы.
Тарифная ставка страхования профессиональной ответственности аудиторов составит 4,776 руб. со 100 руб. страховой суммы.
Аналитическая часть
Постановка задачи
Обобщенную оценку эффективности деятельности страховых организаций дают достигнутые ими финансовые результаты.
Одним из направлений изучения финансовых результатов деятельности организации является анализ прибыли, полученных за несколько отчетных периодов, то есть динамики.
Страховые организации предоставляют в органы статистики сведения о финансовом состоянии, где отражают объем прибыли (убытка). Эта прибыль характеризует конечный финансовый результат и определяется на основе бухгалтерского учета всех хозяйственных операций.
По данным отчетов о прибылях и убытках страховой организации за несколько лет, предоставлены в таблице 3.1, проведем анализ динамики прибыли страховых организаций, для этого рассчитаем следующие показатели:
· абсолютный прирост;
· темп роста;
· темп прироста;
· абсолютное значение 1% прироста;
· средние за период уровень ряда, абсолютный прирост, темп роста и прироста;
Таблица 3.1
Деятельность страховых организаций. [1]
| Число учтенных страховых организаций | |||||||
| Число филиалов страховых организаций (на конец года) | |||||||
| Уставный капитал, млн. руб. | 1642,1 | 16041,6 | 52947,1 | 76336,4 | 130350,3 | 142042,1 | |
| Коэффициент выплат, процентов | 72,7 | 81,5 | 70,5 | 65,4 | 62,4 | 60,9 | |
| Число заключенных договоров страхования, млн. | 113,3 | 90,9 | 90,6 | 99,7 | 106,4 | 138,1 | |
| - в том числе добровольного страхования | 82,5 | 88,8 | 86,7 | 96,4 | 89,7 | 77,5 | 103,3 |
| Страховые премии (взносы), млн. руб. | 23641,1 | 170074,1 | 291174,3 | 329877,8 | 470525,7 | 506151,1 | |
| - из них по договорам добровольного страхования, заключенным за счет средств граждан | 3373,7 | 83432,1 | 158374,4 | 148325,4 | 130663,3 | 138333,7 | 99022,4 |
| Выплаты по договорам страхования, млн. руб. | 17193,7 | 201002,7 | 232530,4 | 292346,4 | 293562,8 | 308484,4 | |
| - из них по договорам добровольного страхования, заключенным за счет средств граждан | 2523,8 | 136600,7 | 123309,1 | 115070,9 | 76258,2 | ||
| Страховая сумма по договорам добровольного страхования, млрд. руб. | 974,5 | 12834,2 | 29084,8 | 41977,5 | 93315,2 | ||
| Страховые премии (взносы) по договорам, переданным в перестрахование (без учета ретроцессии), млн. руб. | 1072,9 | 24987,1 | 43034,9 | 53206,5 | 107356,7 | 87391,9 | 83433,5 |
| Прибыль, млн. руб. | 1891,8 | 2352,1 | 16237,5 | ||||
| Убыток, млн. руб. | 96,7 | 262,7 | 412,3 | 424,8 | 779,1 | 1540,3 | 858,6 |
Методика решения задачи
Расчет показателей анализа ряда динамики осуществим по формулам, представленным в таблице 3.2
Таблица 3.2