Понятие матрицы. Типы матриц. Действия с матрицами: сложение, вычитание матриц, умножение матрицы на число, транспонирование матриц, умножение матриц, возведение в степень.
Матрицей называется прямоугольная таблица чисел. Обозначаются прописными буквами А, В, С, …..
Общий вид матрицы, содержащей m строк и n столбцов:
(1) А =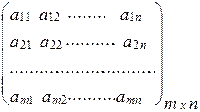 
Внизу справа при необходимости подписываются размеры матрицы: m – количество строк, n – столбцов.
Числа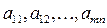 
, составляющие матрицу, называются элементами матрицы.
Матричные элементы обычно обозначаются той же буквой (только строчной), что и сама матрица, а индексы показывают место элемента матрицы в матрице: первый индекс указывает номер строки, а второй – номер столбца, на пересечении которых находится данный матричный элемент. Например, для матрицы
А = 
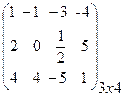элементы 
, 
….
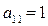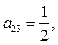Матрицы (так же как и числа) можно вычитать, складывать, перемножать. Поэтому среди матриц есть аналоги нуля и единицы. Нулевой матрицей называется матрица, все элементы которой равны нулю. Она имеет следующий вид и обозначение:
О =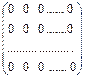 
Если в матрице (1) поменять местами строчки и столбцы (т.е. первую строчку сделать первым столбцом, вторую строку – вторым столбцом и т.д.), то полученная матрица носит название транспонированной по отношению к исходной матрице и обозначается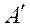 
или 
:
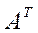А’ =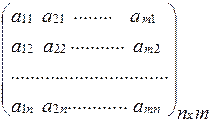 
Квадратная матрица – матрица, число строк и столбцов у которой совпадают. Общий вид квадратной матрицы:
(2) А =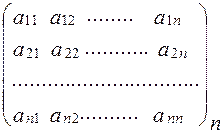 
Числа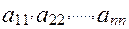 
называются главной диагональю квадратной матрицы.
След матрицы - это сумма элементов главной диагонали квадратной матрицы: Sp(A) = a 11 + a 22 +... + a ii +... + a nn
Дана квадратная матрица A размерностью 3
А =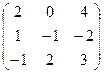 
Решение:
Чтобы вычислить след исходной матрицы, нужно сложить элементы на главной диагонали:
Sp(A) = 2 - 1 + 3 = 4
Ответ: След матрицы A равен 4
Единичной называется такая квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю:
(3) Е =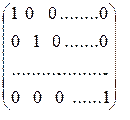 
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка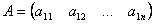 
, называется матрицей – строкой(или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
.
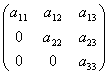Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например,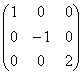 
или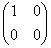 
.
Операции с матрицами
1. Сумма матриц: А + В.
Складывать можно только матрицы одного размера. При сложении двух матриц одного размера получается матрица того же размера, элементы которой равны сумме элементов слагаемых матриц, стоящих на соответствующих местах.
Пример.
Пусть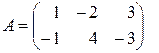 
, 
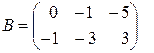. Тогда
А + В =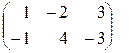 
+ 
= 
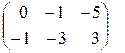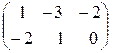
Аналогично определяется вычитание матриц:
А – В = –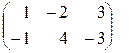 
= 
.
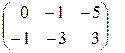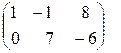2. Умножение числа на матрицу.
При умножении числа на матрицу каждый ее элемент умножается на это число.
Пример.
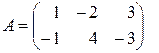, тогда 
.
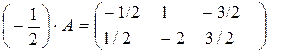Матричные уравнения
Это уравнения, в которых неизвестной является матрица.
Пример. Даны матрицы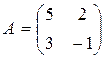 
и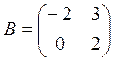 
. Найти матрицу 
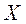, удовлетворяющую следующему матричному уравнению 
.
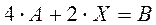Решение. Сначала рассматриваем это уравнение как обычное числовое и находим формулу для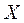 
. Затем действия, предписываемые этой формулой, выполняем по правилам действий с матрицами. Решая обычным способом уравнение 
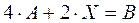, получаем 
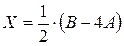. По правилу умножения числа на матрицу 
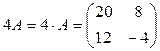, по правилу вычитания матриц 
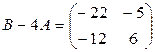. Наконец, по правилу умножения числа на матрицу неизвестная матрица 
.
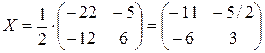3. Умножение матриц: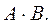 
Далеко не все матрицы можно перемножать.
Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B.
Таким образом, если порядок матрицы A равен m × p, то порядок согласованной с ней матрицы B должен быть равен p × n. Перемножать можно только согласованные матрицы (отметим, что квадратные матрицы одного порядка всегда согласованы).
Произведением двух согласованных матриц A (размера m × p) и B (размера
p × n) называется матрица C (размера m × n), элементы которой вычисляются по правилу: элемент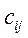 
матрицы С равен сумме попарных произведений элементов i-ой строки матрицы А и j-го столбца матрицы В:
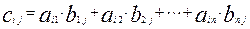
Например, если требуется получить элемент c21, то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы
, 
.
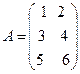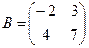Число столбцов матрицы A и число строк матрицы B равны 2, значит, A и B согласованы, причем матрица А∙В будет размера 3х2. Тогда по определению произведение этих матриц А∙В вычисляется следующим образом:
.
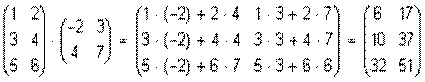Найти в этом случае произведение B∙A невозможно, т.к. матрицы B и A не согласованы. Отсюда следует, что если две матрицы можно перемножить в одном порядке, то это не означает, что их можно перемножать в другом порядке. Можно показать, что в общем случае, даже когда произведения AB и BA определены, они не всегда дают одну и ту же матрицу (даже размерности матриц АВ и ВА могут быть разными).
Свойства операции умножения матриц.
А(В+С)=АВ+АС;
(А+В)С=АС+ВС;
k(АВ)=(kА)В = А(kВ), k - некоторое число;
А(ВС)=(АВ)С;
А · Е =Е·А =А, где Е – единичная матрица.
n×n n×n n×n
Пример. Пусть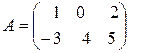 
, 
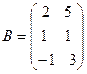. Тогд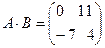а 
, а
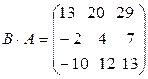(проверьте!). Таким образом 
.
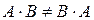Это не значит, что вообще не существует двух таких матриц А и В, для которых АВ=ВА.
Если для пары матриц А и В это свойство все же выполняется, то такие матрицы называются перестановочными (или коммутативными). Например, коммутативными будут матрицы А = 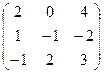и В =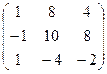 
.
Легко перемножением в том и обратном порядке убедиться, что АВ = ВА =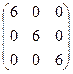 
. Отметим, что квадратные матрицы можно перемножать только если они одного порядка.
Можно указать одну особенную матрицу, которая перестановочна с любой квадратной матрицей. Это введенная выше единичная матрица. Легко в общем виде показать, что для любой квадратной матрицы А имеет место:
А·Е = Е·А = А.
Домашнее задание
№1
Сложить матрицы
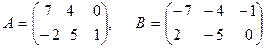
№2
Найти произведение АВ
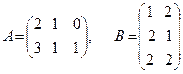
№3
Найти 3А*2В, если
