Наиболее простой опыт, позволяющий установить основные закономерности ползучести, заключается в следующем: образец нагружают постоянной растягивающей нагрузкой при определенной температуре Т и фиксируют изменение во времени его продольных размеров (например, относительно продольной деформации ε). Полученные результаты представляют в виде зависимости «относительная деформация - время». Эти зависимости называют кривыми ползучести, типичные кривые ползучести изображены на рис. 20.1.
| III |
| II |
| ε,% |
| σ2 |
| I |
| t, час |
| σ3 |
| σ1 |
| ε0 |
| III |
Рис. 20.1. Кривые ползучести (1-3 кривые для разных материалов)
В первый момент нагружения возникает лишь мгновенная деформация ε0, которая может быть либо только упругой, либо, кроме упругой, включать и мгновенную пластическую деформацию. В начальный период ползучесть обычно происходит с уменьшающейся скоростью – это участок неустановившейся ползучести (участок I на рис. 20.1). В дальнейшем скорость ползучести в течение некоторого времени остается примерно постоянной (участок II на рис. 20.1), а затем непрерывно возрастает вплоть до разрушения (участок III на рис. 20.1). Длительность каждого из участков ползучести зависит от материала, температуры испытаний и уровня напряжений. Например, для сталей, применяемых в турбостроении, при относительно низких напряжениях (близких к рабочим напряжениям в дисках и лопастях турбины) почти вся деформация накапливается в условиях установившейся ползучести (участок II). Кривая ползучести в таком случае хорошо аппроксимируется прямой. При достаточно высоких температурах и напряжениях кривая ползучести также может быть близка к прямой. Это характерно для так называемой кратковременной ползучести. В некоторых случаях прямолинейный участок на кривой ползучести может вообще отсутствовать.
|
|
Испытания на ползучесть получили широкое распространение, в частности, в связи с проблемой прочности паровых и газовых турбин. Опыты проводились очень большой длительности – известны, например, опыты Робинсона длительностью 100 000 часов (около 12 лет). Но при проектировании новых установок необходимы были данные, позволяющие выбрать размеры деталей и допустимые режимы работы, обеспечивающие потребный срок эксплуатации, полученные на основе испытаний при относительно небольшой длительности. В этой связи одной из первых была задача экстраполяции кривых ползучести на большие длительности.
Для описания процесса ползучести используются различные исходные аналитические выражения, которые получают на основе определенных предположений о характере протекания процесса ползучести. Эти предположения получили название теорий или гипотез.
Если деформация ползучести накапливается в основном на участке установившейся ползучести, то основной характеристикой процесса ползучести может служить скорость ползучести на прямолинейном участке кривой ползучести. Как следует из опытов, зависимость скорости установившейся ползучести при постоянной температуре от напряжений 
и температуры Т может быть представлена в виде:
. (20.1)
Для правой части зависимости (20.1) предложены различные выражения, например:
, (20.2)
, (20.3)
где 
- параметры.
Из соотношения (20.1) можно получить выражение для вычисления деформации ползучести за конечное время t:
|
|
. (20.4)
Рассмотренный подход называют теорией установившейся ползучести, а уравнение (20.1) – основное уравнение этой теории – дает хорошие результаты в оценке деформации ползучести для изделий с очень большим сроком службы и, соответственно, при малых напряжениях или при очень высоких напряжениях и высоких температурах.
Одной из наиболее простых теорий, позволяющих описать ползучесть с учетом всех трех участков, является теория старения, основное уравнение которой имеет вид
, (20.5)
где 
- полная деформация, t – время.
Если предположить, что кривые ползучести, построенные без учета мгновенной начальной деформации подобны, то для деформации ползучести можно записать:
. (20.6)
Функции, входящие в правую часть выражения (20.6), могут быть заданы в виде:
,
где 
- параметры.
Достоинством данной теории является возможность при практических расчетах обойтись без аналитических соотношений вида (20.5) и (20.6). При расчетах для определения деформации, накопленной за заданное время при фиксированном уровне напряжений, можно пользоваться непосредственно кривыми ползучести, построенными либо в обычных координатах, либо в координатах «напряжения - деформация». Способ перестроения иллюстрируют рис.20.2а и рис.20.2б. Кривые ползучести можно перестроить и в координатах «напряжение - время» (рис. 20.2а и рис. 20.2в). При t=0 по оси ординат откладывают напряжения, при котором мгновенная деформация равна выбранному значению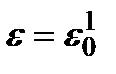 
. Полученные таким образом кривые показывают, как изменяются во времени напряжения, если полная деформация образца остается при испытаниях без изменений.
|
|
Процесс изменения напряжений при постоянстве полной деформации называют релаксацией. Часто термином релаксация называют вообще всякое изменение напряжений при постоянстве условий нагружения или закрепления деталей. Таким образом, кривые ползучести, построенные в координатах «напряжение - время», согласно теории старения представляют собой кривые релаксации.
При переменных напряжениях лучшее совпадение с опытом дает вариант теории старения, называемой теорией течения. Основное уравнение теории течения записывают в виде:
. (20.7)
Из условия подобия кривых ползучести в соответствии с выражением (20.6) получаем:
.
Если же в качестве независимой переменной рассматривать в выражении (20.6) функцию 
, то получаем:
. (20.8)
Выражение (20.8) аналогично выражению (20.1) в теории установившейся ползучести, только масштаб времени изменен.
Результаты испытаний на ползучесть в пределах первого участка кривых ползучести, а также релаксация напряжений более точно описываются уравнениями, полученными на основе теории упрочнения. Общее уравнение этой теории, называемое уравнением состояния, можно записать в виде:
.
Используя предположение о подобии кривых ползучести и выбирая функцию 
в выражении (20.6) степенной, получаем следующее уравнение:
. (20.9)
| σ |
| t2 |
| ε |
| σ |
| а) |
| t1 |
| ε1 |
| ε2 |
| ε3 |
| ε4 |
| σ4 |
| σ3 |
| σ2 |
| σ1 |
| T=const |
| σ4 |
| σ3 |
| σ2 |
| σ1 |
| σ4 |
| ε01 |
| ε4 |
| ε3 |
| ε2 |
| ε1 |
| ε |
| σ2 |
| t |
| σ3 |
| σ1 |
| T=const |
|
|
|
|
|
|
|
|
|
|
|
|
| t |
| T=const |
|
| б) |
| в) |
Рис. 20.2. Различные представления кривых ползучести
Функцию 
выбирают тоже обычно степенной - 
или экспоненциальной 
. В приведенных выражениях 
- параметры.
Рассмотренные теории ползучести позволяют определить деформацию ползучести за заданное время при заданной температуре или изменение напряжений при фиксированных условиях нагружения или закрепления деталей. Эти теории основываются на обобщении результатов опытов на ползучесть при растяжении. Во многих деталях и элементах конструкции накопление деформаций ползучести происходит в условиях переменных напряжений и температур и при объемном напряженном состоянии. Предлагаемые в этих случаях методы расчетов значительно сложнее рассмотренных, относятся чаще всего к частным задачам и требуют дальнейшего развития и экспериментального обоснования.
Рассмотрим использование изложенных подходов при оценке работоспособности деталей и конструкций. Если работоспособность элемента конструкции может быть нарушена из-за значительного изменения формы и размеров вследствие ползучести, то обеспечение работоспособности заключается в выборе такого уровня напряжений, чтобы при определенной температуре и длительности эксплуатации деформация ползучести не превышала некоторую предельную величину. Это условие можно записать в виде
. (20.10)
По теории установившейся ползучести можно получить, используя выражения (20.2) и (20.4), следующие соотношение:
.
Откуда
. (20.11)
Наибольшее напряжение, которое при данной температуре и за заданное время не вызывает деформации детали, превышающей допускаемую, называют условным пределом текучести по допускаемой деформации.
Предел ползучести для данного материала зависит от температуры и величины допускаемой деформации ползучести в течение срока эксплуатации элемента конструкции. В табл. 20.2 приведены величины допускаемой деформации ползучести для некоторых конструктивных элементов.
Таблица 20.2
| Конструктивный элемент | Время работы t, час | Допускаемая деформация 
|
| Авиационные газовые турбины | 300…500 | 0,001 |
| Диски турбин | 100 000 | 0,0001 |
| Паропроводы | 100 000 | 0,003 |
| Цилиндры паровых турбин | 100 000 | 0,001 |
Для некоторых элементов конструкций удобнее регламентировать скорость установившейся ползучести. По зависимости (20.1) находим:
.
Откуда имеем
.
Наибольшее напряжение, которое при заданной температуре не приводит к скорости деформации, превышающей допустимую, называют условным пределом ползучести по допускаемой скорости установившейся ползучести.
Например, для турбинных дисков, болтов, фланцев, цилиндров паровых турбин допускаемая скорость ползучести равна 
.