Содержание
Условие задачи. 3
Теоретическое введение. 4
Решение. 5
Вывод. 14
Список используемой литературы.. 14
Условие задачи
Прочность Y (кг/см2) бетона при испытании цилиндрических образцов в зависимости от отношения X = h / a высоты h к диаметру a оказалась равной:
| X | 1,5 | 2,9 | 3,1 | 3,2 | 3,4 | 3,5 | 3,6 | 4,2 | |
| Y |
На основании опытных данных требуется:
1. Построить корреляционное поле. По характеру расположения точек в корреляционном поле подобрать вид функции регрессии.
2. Написать уравнение функции регрессии.
3. Определить тесноту корреляционной связи между рассматриваемыми признаками.
4. Проверить адекватность модели.
5. Построить линию регрессии в системе координат.
Теоретическое введение
Регрессионный анализ - это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется у при изменении любого из xi, и имеет вид:
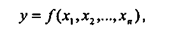
где у - зависимая переменная (она всегда одна);
хi - независимые переменные (факторы) (их может быть несколько).
Если независимая переменная одна - это простой регрессионный анализ. Если же их несколько (п  2), то такой анализ называется многофакторным.
2), то такой анализ называется многофакторным.
В ходе регрессионного анализа решаются две основные задачи:
построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x 1, x 2, …, xn.
оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.
Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы.
В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный - одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.
Регрессионный анализ - один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, x l ,x 2 ,...,xn; y должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными.
Решение
Решение поставленной задачи будет производится с помощью программного обеспечения MicrosoftOffice, а именно средствами приложения Excel.
1) На основании исходных данных построим корреляционное поле:

Рисунок 1 Корреляционное поле
Исходя из характера расположения точек, можно предположить, что наилучшим образом данную зависимость будет описывать степенная или логарифмическая регрессионная функция. Для проверки данного предположения сформируем гипотезы о форме связи и произведём расчёт параметров для четырёх различных типов функций:
· Линейной
· Степенной
· Логарифмический
· Показательной
а) Линейная парная регрессия рассчитывается по следующей формуле:

Для расчёта параметров a и b используем формулы:


Где 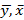 – средние значения велечин, представленные в Таблице 1.
– средние значения велечин, представленные в Таблице 1.
Таблица 1
| Линейная регрессия y = bx+a | ||||
| X | Y | X2 | XY | |
| 1,5 | 2,25 | |||
| 2,9 | 8,41 | 1792,2 | ||
| 3,1 | 9,61 | |||
| 3,2 | 10,24 | 2118,4 | ||
| 3,4 | 11,56 | 2376,6 | ||
| 3,5 | 12,25 | 2509,5 | ||
| 3,6 | 12,96 | |||
| 4,2 | 17,64 | 3301,2 | ||
| Среднее | 3,155556 | 10,43556 | 2200,989 |
Вычислим значения коэффициентов регрессии a и b:


Следовательно линейное уравнение регрессии будет выглядеть следующим образом:


Рисунок 2 Линейная парная регрессия
б) Степенная парная регрессия рассчитывается по следующей формуле:

Для определения параметров a и b необходимо линеаризировать его, для чего логарифмируем его правую и левую части:

Обозначим  ,
,  ,
, 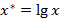
Тогда:

Для расчёта параметров a и b используем формулы:
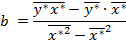

Таблица 2
| X | Y | X*=lg(x) | Y*=lg(y) | X*2 | X*Y* | |
| 1,5 | 0,176 | 2,763 | 0,031 | 0,487 | ||
| 2,9 | 0,462 | 2,791 | 0,214 | 1,291 | ||
| 0,477 | 2,818 | 0,228 | 1,345 | |||
| 3,1 | 0,491 | 2,826 | 0,241 | 1,389 | ||
| 3,2 | 0,505 | 2,821 | 0,255 | 1,425 | ||
| 3,4 | 0,531 | 2,844 | 0,282 | 1,512 | ||
| 3,5 | 0,544 | 2,856 | 0,296 | 1,554 | ||
| 3,6 | 0,556 | 2,889 | 0,309 | 1,607 | ||
| 4,2 | 0,623 | 2,895 | 0,388 | 1,805 | ||
| Среднее | 3,156 | 685,000 | 0,485 | 2,834 | 0,249 | 1,379 |
Вычислим значения коэффициентов регрессии a и b:



Следовательно степенное уравнение регрессии будет выглядеть следующим образом:


Рисунок 3 Степенная парная регрессия
в) Уравнение логарифмическойрегрессииимеет следующий вид:

Для определения параметров a и b обозначим  и представим уравнение в следующем виде:
и представим уравнение в следующем виде:

Для расчёта параметров a и b используем формулы:


Таблица 3
| X | Y | X*=lg(x) | X*2 | X*Y | |
| 1,5 | 0,176 | 0,031 | 102,133 | ||
| 2,9 | 0,462397998 | 0,213811908 | 285,76 | ||
| 0,477 | 0,228 | 313,946 | |||
| 3,1 | 0,491 | 0,241 | 329,212 | ||
| 3,2 | 0,505 | 0,255 | 334,409 | ||
| 3,4 | 0,531 | 0,282 | 371,504 | ||
| 3,5 | 0,544 | 0,296 | 390,097 | ||
| 3,6 | 0,556 | 0,309 | 431,134 | ||
| 4,2 | 0,623 | 0,388 | 489,874 | ||
| Среднее | 3,156 | 0,485 | 0,249 | 338,675 |
Вычислим значения коэффициентов регрессии a и b:


Следовательно логарифмическое уравнение регрессии будет выглядеть следующим образом:


Рисунок 4Логарифмическая регрессия
г) Уравнение логарифмической регрессии имеет следующий вид:

Для определения параметров a и b необходимо линеаризировать его, для чего прологарифмируем правую и левую части уравнения:

Обозначим  ,
,  ,
, 
Тогда:
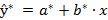
Для расчёта параметров a и b используем формулы:
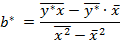
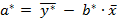
Таблица 4
| X | Y | Y*=lg(y) | X2 | XY* | |
| 1,5 | 2,763 | 2,25 | 4,145 | ||
| 2,9 | 2,791 | 8,41 | 8,094 | ||
| 2,818 | 8,455 | ||||
| 3,1 | 2,826 | 9,61 | 8,761 | ||
| 3,2 | 2,821 | 10,24 | 9,027 | ||
| 3,4 | 2,844 | 11,56 | 9,671 | ||
| 3,5 | 2,856 | 12,25 | 9,994 | ||
| 3,6 | 2,889 | 12,96 | 10,401 | ||
| 4,2 | 2,895 | 17,64 | 12,161 | ||
| Среднее | 3,156 | 685,000 | 2,834 | 10,436 | 8,968 |
Вычислим значения коэффициентов регрессии a и b:




Следовательно степенное уравнение регрессии будет выглядеть следующим образом:


Рисунок 5Показательная регрессия
Оценка тесноты связи с помощью показателей корреляции и детерминации
а) Коэффициент корреляции для линейной регрессии определяется по формуле:

Где 
Тогда:



Коэффициент детерминации для линейной регрессии рассчитывается по формуле:
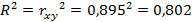
б) Коэффициент корреляции для степенной регрессии определяется по формуле:

Где

Тогда:

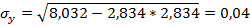

Коэффициент детерминации для степенной регрессии рассчитывается по формуле:

в) Коэффициент корреляции для логарифмической регрессии определяется по формуле:

Где 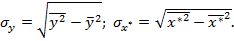
Тогда:



Коэффициент детерминации для логарифмической регрессии рассчитывается по формуле:

г) Коэффициент корреляции для показательной регрессии определяется по формуле:

Где

Тогда:
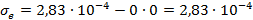
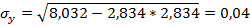

Коэффициент детерминации для показательной регрессии рассчитывается по формуле:
