Одно из удивительных и трудно доказываемых
|
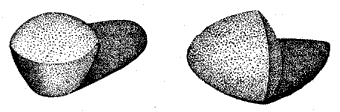
| Рис. 8. Два тела постоянной ширины. |
свойств состоит, в том, что все кривые одной и той же постоянной ширины n имеют одинаковые периметры. Поскольку окружность принадлежит к числу кривых постоянной ширины, периметр любой кривой постоянной ширины n равен длине окружности диаметра n, то есть величине 
n.
Трехмерные аналоги кривых постоянной ширины называются телами постоянной ширины. Сфера — не единственное тело, которое может вращаться внутри куба, все время, касаясь всех шести его граней. Этим же свойством обладают все тела постоянной ширины. Простейшим примером несферического тела постоянной ширины может служить тело, образующееся при вращении треугольника Рело вокруг одной из его осей симметрии (см. левое тело на рис. 8). Существует бесконечно много и других тел постоянной ширины. Те из них, которые имеют наименьший объем при данной ширине, получаются из правильного тетраэдра, так же как треугольник Рело — из равностороннего треугольника: сначала на каждую грань тетраэдра помещают сферические шапочки, а затем слегка скругляют ребра. Ребра либо исходят из одной вершины, либо образуют треугольник. Примером такого искривленного тетраэдра постоянной ширины может служить тело, изображенное на (рис. 8) справа. Поскольку все кривые одинаковой постоянной ширины имеют один и тот же периметр, может показаться, будто и все тела одинаковой постоянной ширины имеют одну и ту же площадь поверхности. Однако такое утверждение не верно. Как показал известный математик Герман Минковский, все тени, отбрасываемые телами постоянной ширины (предполагается, что лучи солнца параллельны, а тень падает на плоскость, перпендикулярную лучам), имеют форму кривых постоянной ширины. Периметры всех теней, отбрасываемых телами одной и той же постоянной ширины, одинаковы (и равны d, где d — ширина тела). Выпуклая фигура, которая может вращаться внутри многоугольника или многогранника, касаясь все время всех его сторон, называется ротором. Мы видели, что треугольник Рело является ротором минимальной площади для квадрата. Ротор минимальной площади для равностороннего треугольника показан на (рис. 9) слева. Это — фигура в форме линзы (разумеется, ее контур не является кривой постоянной ширины), образованная дугами двух окружностей, радиус которых равен высоте треугольника (каждая дуга составляет 60°). Важно заметить, что концы ротора при вращении описывают весь периметр треугольника, не закругляя углов. К сожалению, технологи-
|
| Рис. 9. Ротор наименьшей площади внутри равностороннего треугольника. Справа показан отрезок прямой, вращающийся внутри гипоциклоиды. |
ческие трудности не позволяют изготовлять сверла в форме ротора для равностороннего треугольника, но сверла, позволяющие делать отверстия в форме правильных пяти-, шести и даже восьмиугольников с незакругленными углами, имеются. Доказано, что в трехмерном пространстве существуют несферические роторы для правильного тетраэдра, октаэдра и куба, но не для додекаэдра и икосаэдра. Относительно роторов в пространствах большего числа измерений почти ничего не известно.
Непосредственное отношение к теории роторов имеет знаменитая задача об игле, названная в честь сформулировавшего ее еще в 1917 году японского математика Какейя «проблемой Какейя». Заключается она в следующем: в какой плоской фигуре, имеющей минимальную площадь, можно повернуть на 360° единичный отрезок прямой? Такой отрезок, очевидно, можно повернуть на 360° внутри окружности диаметром 1, но ограничиваемый ею круг не будет иметь минимально возможную площадь.
Довольно долго математики считали, что решением проблемы Какейя служит кривая, изображенная на (рис. 9 справа), ее площадь равна половине площади круга. (Эта кривая называется гипоциклоидой. Такую кривую описывает точка окружности, катящейся без скольжения внутри большей окружности, если диаметр меньшей окружности составляет 1/3 или 2/3 диаметра большей.) Отломив кусок спички нужных размеров, вы на опыте убедитесь в том, что ее можно повернуть внутри гипоциклоиды как некий одномерный ротор. Обратите внимание, что концы спички будут все время оставаться на контуре гипоциклоиды.
Сенсация произошла в 1927 году, через десять лет после того, как Какейя поставил свою проблему. «Виновником» ее стал А. С. Безикович. Он доказал, что проблема Какейя... не имеет решения! Точнее, из результатов Безиковича следовало, что не существует кривой с минимальной площадью, внутри которой единичный отрезок можно было бы повернуть на 360°. Сколь бы малой ни была площадь фигуры, всегда можно построить другую фигуру с еще меньшей площадью, внутри которой единичный отрезок также сумеет развернуться на 360°. Представим себе отрезок, простирающийся от Земли до Луны. По теореме Безиковича, его можно повернуть на 360° внутри фигуры, площадь которой меньше площади почтовой марки с изображением Линкольна. Если и этого вам покажется мало, то тот же отрезок можно повернуть на 360° внутри фигуры, площадь которой меньше площади, занимаемой на почтовой марке носом Линкольна.
Литература:
1. Александров А.Д., Нецветаева Н.Ю. Геометрия. М:,1990.
2. Атанасян Л.С., Базылев В.Т. Геометрия, ч. 1, М:, Просвещение 1986.
3. Данцер Л., Грбнбаум Б., теорема Хелли.- М.: Мир,1968.
4. Моденов П.С. Аналитическая геометрия. М.: 1969.
5. Энциклопедический словарь юного математика/Сост. А.П. Савин.- М.: Педагогика,1985.
6. Математическая энциклопедия: Гл. ред. И.М. Виноградов.- М,: «Советская энциклопедия», 1984.
7. Бляшке В. Круг и шар.- М.: Мир, 1968.