 Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,41•10–3 м3/моль.
Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,41•10–3 м3/моль.
По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:
NA=6,022•1023 моль-1
Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений p1, p2,..., рn входящих в нее газов:
p = p1 + p2 +...+ рn
Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
31  удовлетворяет только идеальный газ, и оно является уравнением состояния идеального газа, которое называется также уравнением Клайперона – Менделеева.
удовлетворяет только идеальный газ, и оно является уравнением состояния идеального газа, которое называется также уравнением Клайперона – Менделеева.
32 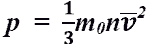 основное уравнение молекулярно-кинетической теории идеальных газов
основное уравнение молекулярно-кинетической теории идеальных газов
33 Закон Максвелла описывается некоторой функцией f(ν), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν +d ν, т. е.

откуда

Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям:
 (1)
(1)
Из (1) видно, что конкретный вид функции зависит от вида газа (от массы молекулы) и от параметра состояния (от температуры Т).
График функции (1) приведен на рис. 1. Так как при возрастании ν множитель exp[–m0 ν 2/(2kT)] уменьшается быстрее, чем увеличивается множитель ν 2, то функция f(ν), начинаясь от нуля, достигает максимума при ν B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно ν B. 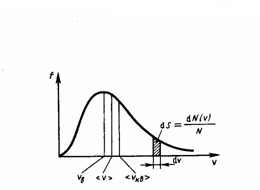 Относительное число молекул dN(ν)/N, со скоростями, лежащими в интервале от ν до ν +d ν, рассчитывается как площадь заштрихованной полоски на рис. 1. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция f(ν) удовлетворяет условию нормировки
Относительное число молекул dN(ν)/N, со скоростями, лежащими в интервале от ν до ν +d ν, рассчитывается как площадь заштрихованной полоски на рис. 1. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция f(ν) удовлетворяет условию нормировки

Скорость, при которой максимальна функция распределения молекул идеального газа по скоростям, называется наиболее вероятной скоростью, значение которой можно найти продифференцировав выражение (1) (постоянные множители опускаем) по аргументу ν, при этом приравняв результат нулю и используя условие для максимума выражения f(ν):


Значения ν =0 и ν =∞ соответствуют минимумам выражения (1), а значение ν, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость ν B:
 (2)
(2)
Из формулы (2) мы видим, что при возрастании температуры максимум функции распределения молекул по скоростям (рис. 2) движется вправо (при этом становится больше значение наиболее вероятной скорости). Однако площадь, которая ограничена кривой, не меняется, поэтому кривая распределения молекул по скоростям при повышении температуры будет растягиваться и понижаться.
Средняя скорость молекулы < ν > (средняя арифметическая скорость) определяется по формуле

Подставляя сюда f(ν) и интегрируя, получаем
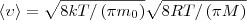 (3)
(3)
Скорости, которые характеризуют состояние газа: 1) наиболее вероятная  2)средняя
2)средняя  3) средняя квадратичная
3) средняя квадратичная  (рис. 1). Исходя из распределения молекул по скоростям
(рис. 1). Исходя из распределения молекул по скоростям
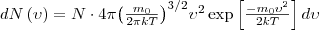 (4)
(4)
найдем распределение молекул газа по значениям кинетической энергии ε. С этой целью перейдем от переменной ν к переменной ε=m0v2/2. Подставив в (4)  и
и  , получим
, получим

где dN(ε) — число молекул, которые имели кинетическую энергию поступательного движения, заключенную в интервале от ε до ε + dε.
Значит, функция распределения молекул по энергиям теплового движения

Средняя кинетическая энергия <ε> молекулы идеального газа

т. е. получили результат, совпадающий с формулой о средней кинетической энергии движения одной молекулы идеального газа, выводимой из молекулярно-кинетической теории.
34. При выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям делалось предположение, что внешние силы не действуют на молекулы газа, поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли. Сила тяжести, с одной стороны, и тепловое движение молекул — с другой, приводят газ к некоторому стационарному состоянию, при котором давление газа с высотой уменьшается.
Выведем закон изменения давления с высотой, предполагая при этом, что масса всех молекул одинакова, поле тяготения однородно и температура постоянна.
Если атмосферное давление на высоте h равно р (рис. 1), то на высоте h+dh оно равно p+dp (при dh>0 dp<0, так как давление с высотой уменьшается). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с основанием площадью 1 м2:

где ρ — плотность газа на высоте h (dh настолько мало, что при изменении высоты в этом интервале плотность газа можно считать постоянной). Значит,
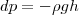 (1)
(1)
Зная уравнение состояния идеального газа pV=(m/M) RT (m — масса газа, М — молярная масса газа), находим, что
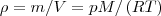
Подставив это выражение в (1), получим
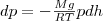 или
или 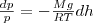
С изменением высоты от h1 до h2 давление изменяется от р1 до р2 (рис. 67), т. е.

или
 (2)
(2)
Выражение (2) называется барометрической формулой. Она позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту: Так как высоты считаются относительно уровня моря, где давление считается нормальным, то выражение (2) может быть представлено в виде
 (3)
(3)
где р — давление на высоте h.
Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на применении формулы (3). Из этой формулы следует, что чем тяжелее газ, тем давление с высотой убывает тем быстрее.
Барометрическую формулу (3) можно преобразовать, если воспользоваться формулой p=nkT:

где n – концентрация молекул на высоте h, n0 – то же, на высоте h=0. Так как M=m0NA (NA – постоянная Авогадро, m0 – масса одной молекулы), a R=kNA, то
 (4)
(4)
где m0gh=P — потенциальная энергия молекулы в поле тяготения, т. е.
 (5)
(5)
Выражение (5) называется распределением Больцмана для внешнего потенциального поля. Из него видно, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.
Если частицы находятся в состоянии хаотического теплового движения и имеют одинаковую массу и, то распределение Больцмана (5) применимо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
35 Молекулы газа, находясь в хаотическом движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, называемым длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с очень большим числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 1). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).
Так как за 1 с молекула в среднем проходит путь, который равен средней арифметической скорости <v>, и если < z > — среднее число столкновений, которые одна молекула газа делает за 1 с, то средняя длина свободного пробега будет

Для определения < z > представим себе молекулу в виде шарика диаметром d, которая движется среди других как бы застывших молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстояниях, равных или меньших d, т. е. лежат внутри так называемого ломаного цилиндра радиусом d (рис. 2).
Среднее число столкновений за 1 с равно числу молекул в объеме, так называемого ломаного цилиндра:

где n — концентрация молекул, V = πd2<v>,где <v> — средняя скорость молекулы или путь, пройденным ею за 1 с). Таким образом, среднее число столкновений

Расчеты показывают, что при учете движения других молекул

Тогда средняя длина свободного пробега
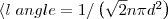
т. е. < l > обратно пропорциональна концентрации n молекул. С другой стороны, p=nkt. Значит,

36 В термодинамически неравновесных системах возникают особые необратимые
процессы, называемые явлениями переноса, в результате которых происходит простран-
ственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопро-
водность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и
внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномерными явле-
ниями переноса. Систему отсчета выберем так, чтобы ось х была ориентирована в направлении переноса. 1. Теплопроводность. Если в первой области газа средняя кинетическая энергия молекул больше, чем во второй, то вследствие постоянных столкновений молекул с течением времени происходит процесс выравнивания средних кинетических энергий молекул, т. е., выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье:
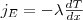 (1)
(1)
где jE — плотность теплового потока — величина, которая определяется энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х, λ — теплопроводность, — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус говорит о том, что во время теплопроводности энергия перемещается в направлении убывания температуры (поэтому знаки jE и – противоположны). Теплопроводность λ равна плотности теплового потока при градиенте температуры, равном единице.
Можно показать, что
 (2)
(2)
где сV — удельная теплоемкость газа при постоянном объеме (количество теплоты, которое необходимо для нагревания 1 кг газа на 1 К при постоянном объеме), ρ — плотность газа, < ν > — средняя скорость теплового движения молекул, < l > — средняя длина свободного пробега.
2. Диффузия. При происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия есть обмен масс частиц этих тел, при этом явление возникает и продолжается, пока существует градиент плотности. Во времена становления молекулярно-кинетической теории по вопросу явления диффузии возникли противоречия. Поскольку молекулы перемещаются в пространстве с огромными скоростями, то диффузия должна происходить очень быстро. Если же открыть в комнате крышку сосуда с пахучим веществом, то запах распространяется довольно медленно. Но здесь нет противоречия. При атмосферном давлении молекулы обладают малой длиной свободного пробега и, при столкновениях с другими молекулами, приемущественно «стоят» на месте.
Явление диффузии для химически однородного газа подчиняется закону Фика:
 (3)
(3)
где jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), dρ/dx — градиент плотности, который равен скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус говорит о том, что перенос массы происходит в направлении убывания плотности (поэтому знаки jm и dρ/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов,
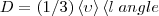 (4)
(4)
3. Внутреннее трение (вязкость). Суть механизма возникновения внутреннего трения между параллельными слоями газа (жидкости), которые движущутся с различными скоростями, есть в том, что из-за хаотического теплового движения осуществляется обмен молекулами между слоями, в результате чего импульс слоя, который движется быстрее, уменьшается, который движется медленнее — увеличивается, что приводит к торможению слоя, который движется быстрее, и ускорению слоя, который движется медленнее.
Как известно, сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона:
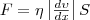 (5)
(5)
где η — динамическая вязкость (вязкость), d ν /dx — градиент скорости, который показывает быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S — площадь, на которую действует сила F.
Согласно второму закону Ньютона взаимодействие двух слоев можно рассматривать как процесс, при котором в единицу времени от одного слоя к другому передается импульс, который по модулю равен действующей силе. Тогда выражение (5) можно записать в виде
 (6)
(6)
где jp — плотность потока импульса — величина, которая определяется определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х, d ν /dx — градиент скорости. Знак минус говорит о том, что импульс переносится в направлении убывания скорости (поэтому знаки jp и d ν /dx противоположны).
Динамическая вязкость η численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле
 (7)
(7)
Из сопосавления формул (1), (3) и (6), которые описывают явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Эти законы были известны еще задолго до того, как они были обоснованы и получены из молекулярно-кинетической теории, которая позволила установить, что внешнее сходство их математических выражений является следствием общностью лежащего в основе явлений теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения и столкновений друг с другом.
Рассмотренные законы Фурье, Фика и Ньютона не вскрывают молекулярно-кинетической сути коэффициентов λ, D и η. Выражения для коэффициентов переноса получаются из кинетической теории. Они записаны без вывода, поскольку строгое и формальное рассмотрение явлений переноса довольно громоздко, а качественное — не имеет смысла. Формулы (2), (4) и (7) дают связь коэффициентов переноса и характеристики теплового движения молекул. Из этих формул следуют простые зависимости между λ, D и η:
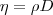 и
и 
37 Величины, однозначно определяемые параметрами состояния, называются
функциями состояния. Важнейшей функцией состояния является внутренняя
энергия системы. Внутренней энергией системы называют общий запас энер-
гии, которым обладает термодинамическая система. Из молекулярно-кинетической теории
известно, что внутренняя энергия тела складывается из кинетической энергии движения молекул и потенциаль-
ной энергии их взаимного расположения. Покажем, что внутренняя энергия является функцией состояния.
Предположим, что термодинамическая система нахо-
дится в состоянии 1 с параметрами p 1, V 1, T 1. Значение
внутренняя энергия U 1 = U (p 1, V 1, T 1). Переведем рассматриваемую систему из состояния 1 в состояние 2 с параметрами p 2, V 2, T 2. Значение энергии в этом случае
U 2 = U (p 2, V 2, T 2). При переходе системы из первого состояния во второе дельта U = U 2 - U 1 будет иметь одно и то же значение, вне зависимости от того, каким путем совершается переход из одного состояния в другое по abc или по adc. Это справедливо для всех функций состояния, то есть для любой функции состояния. Элементарная работа dA при элементарном изменении
объема ΔV определяется как dA = Fdl = pSdl = pdV, где S –
площадь поршня; Sdl = dV – изменение объема системы; p = const.
Полную работа найдем интегрированием данного выражения:
 Количеством теплоты Q, полученным телом, называют изменение внутренней энергии тела в результате теплообмена.
Количеством теплоты Q, полученным телом, называют изменение внутренней энергии тела в результате теплообмена.