дить только при наличии разности температур между ними. Тепловой поток
всегда направлен от горячего тела к холодному.
Количество теплоты Q является энергетической величиной [ Дж ].
Процессы, связанные с поглощением теплоты: нагревание, плавление, парообразование. С выделением – охлаждение, кристаллизация, конденсация, сгорание топлива. При нагревании (охлаждении) – 
; плавлении
(кристаллизации) –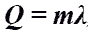 
; парообразовании (конденсации) – Q = rm; сжигании топлива – Q = gm, где с, λ, r, g – соответственно удельная теплоемкость,
удельная теплота плавления, удельная теплота парообразования, удельная теплота
сгорания топлива (табличные величины).
Для замкнутой системы (дельта Ui = Qi) суммарная внутренняя энергия не меняется:
делтаU 1 + дельта U 2 + дельта U 3 +... + дельта Un = 0 следует Q 1 + Q 2 + Q 3 +...+ Qn = 0 – уравнение теплового
Баланса
38. Нулевое начало термодинамики. Равновесное состояние системы – состоя-
ние системы, при котором все подсистемы (части системы) характеризуются одинаковыми значениями термодинамических параметров, неизменными в течение сколь угодно долгого времени.
Свойство термодинамической системы находящейся в термодинамическом
равновесии с другой системой описывается важной характеристикой (параметром)
состояния системы – температурой. Если две системы находятся в равновесии,
их температуры по определению одинаковы. Разность температур показыва-ет степень отклонения систем от равновесия.
Возможность введения понятия температуры обусловлено нулевым началом
термодинамики, являющимся обобщением эмпирического опыта: если две системы находятся в состоянии термодинамического равновесия с третьей системой, то они пребывают в равновесии и друг с другом. первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил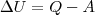 
39 В механике введилось понятие числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения.
В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения.
При любом числе степеней свободы данной молекулы три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, значит на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0> (энергия поступательного движения молекул):
В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i = i пост+ i вращ+2 i колеб
В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.
Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул:
(1)
Внутренняя энергия для произвольной массы m газа.
где М — молярная масса, ν — количество вещества.
40 Удельная теплоемкость вещества — величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг•К)).
Молярная теплоемкость —величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:
(1)
где ν =m/М—количество вещества.
Единица молярной теплоемкости — джоуль на моль•кельвин (Дж/(моль•К)).
Удельная теплоемкость с связана с молярной теплоемкостью Сm, соотношением
(2)
где М — молярная масса вещества.
Выделяют теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.
Запишем выражение первого начала термодинамики для одного моль газа с учетом (1) и δA=pdV
(3)
Если газ нагревается при постоянном объеме, то dV=0 и работа внешних сил равна также равна нулю. Тогда газу сообщаемая извне теплота идет только на увеличение его внутренней энергии:
(4)
т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии одного моль газа при повышении его температуры на 1 К. Поскольку Um=(i /2)RT, то
(5)
Если газ нагревается при постоянном давлении, то выражение (3) можно представить в виде
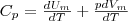
Учитывая, что (Um/dT) не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна СV (см. (4)), и дифференцируя уравнение Клапейрона — Менделеева pVm=RT (42.4) по T (p=const), получаем
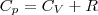(6)
Выражение (6) называется уравнением Майера; оно говорит о том, что Сp всегда больше СV ровно на величину молярной газовой постоянной. Это объясняется тем, чтобы осуществить нагревание газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (5), формулу (6) можно записать в виде
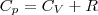(7)
При исследовании термодинамических процессов важно знать характерное для каждого газа отношение Сp к СV:
(8)
Из формул (5) и (7) следует, что молярные теплоемкости зависят лишь от числа степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, которое проявляется в теплоемкости, зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы.
По закону равномерного распределения энергии по степеням свободы, для комнатных температур СV = (7/2)R. Из качественной экспериментальной зависимости молярной теплоемкости СV водорода (рис. 1) следует, что СV следующим образом зависит от температуры: при низкой температуре (≈50 К) СV = (3/2)R, при комнатной — CV = (5/2)R (вместо расчетных (7/2)R) и при очень высокой — СV= (7/2)R. Это можно объяснить, сделав предположение, что при низких температурах наблюдается только поступательное движение молекул, при комнатных — добавляется их вращение, а при высоких — к данным двум видам движения добавляются еще колебания молекул.
41 Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е.
Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии:
т.к. CV=dUm/dt,
Тогда для произвольной массы газа получим
(1)
Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V1 до V2 равна
(2)
и равна площади заштрихованного прямоугольника (рис. 2). Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то
и 
откуда
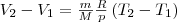
Тогда выражение (2) для работы изобарного расширения примет вид
(3)
Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2 —T1 = 1К, то для 1 моль газа R=A, т. е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К. В изобарном процессе при сообщении газу массой m количества теплоты
его внутренняя энергия возрастает на величину (т.к. CV=dUm/dt)
При этом газ совершит работу, определяемую выражением (3).
Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта:
Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс.
Исходя из формул для работы газа и уравнения Менделеева-Клайперона найдем работу изотермического расширения газа:
Так как при Т=const внутренняя энергия идеального газа не изменяется:
то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:
(4)
Значит, для того чтобы при расширении газа температура не становилась меньше, к газу в течение изотермического процесса необходимо подводить количество теплоты, равное внешней работе расширения.
Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. Таковым, например, можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько большая по значению, что обмен энергией между средой и волной произойти не успевает. Адиабатические процессы происходят в двигателях внутреннего сгорания (сжатие и расширение горючей смеси в цилиндрах), в холодильных установках и т. д.
Из первого начала термодинамики (δQ=dU+δA) для адиабатического процесса следует, что
(1)
т. е. внешняя работа совершается за счет изменения внутренней энергии системы.
Используя формулы δA=pdV и CV=dUm/dT, для произвольной массы газа перепишем уравнение (1) в виде
(2)
применив дифференцирование уравнение состояния для идеального газа pV=(m/M)RT получим
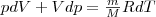(3)
Исключим из (2) и (3) температуру Т.
Разделив переменные и учитывая, что Сp/СV=γ, найдем
Проинтегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, и потенцируя, придем к выражению
или 
Так как состояния 1 и 2 выбраны произвольно, то можно записать
(4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.
Для перехода к переменным Т, V или p, Т исключим из (55.4) с помощью уравнения Менделеева-Клапейрона
соответственно давление или объем:
(5)
(6)
Выражения (4) — (6) представляют собой уравнения адиабатического процесса. В них безразмерная величина
(7)
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i =3, γ=1,67. Для двухатомных газов (Н2, N2, О2 и др.) i =5, γ=1,4. Значения γ, вычисленные по формуле (55.7), хорошо подтверждаются экспериментом.
Диаграмма адиабатического процесса (адиабата) в координатах р, V есть гипербола (рис. 1). На рисунке видно, что адиабата (pVγ = const) более крута, чем изотерма (pV = const) по причине, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.
42 Вычислим работу, которую совершает газ в адиабатическом процессе. Запишем уравнение (1) в виде
Если газ адиабатически расширяется от объема V1 до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа
(8)
Используя те же приемы, что и при выводе формулы (5), выражение (8) для работы при адиабатическом расширении можно привести к виду
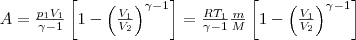
где p1V1=(m/M)RT1
Работа, которую совершает газом при адиабатическом расширении 1—2 (определяется площадью, заштрихованной на рис. 2), меньше, чем при изотермическом, по причине, что при адиабатическом расширении осуществляется охлаждение газа, тогда как при изотермическом — температура поддерживается постоянной за счет притока извне такого же количества теплоты.
Рассмотренные изобарный, изохорный, изотермический и адиабатический процессы имеют общую особенность — они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны СV и Сp, в изотермическом процессе (dT=0) теплоемкость равна ±∞, в адиабатическом (δQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается неизменной, называется политропным.
Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const) можно вывести уравнение политропы:
(9)
где n=(С—Сp)/(С—СV)—показатель политропы. Очевидно, что при С=0, n=γ, из (55.9) получается уравнение адиабаты; при С = 0, n = 1 — уравнение изотермы; при С=Сp, n=0 —уравнение изобары, при С=СV, n=±∞ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.
43 В термодинамических рассуждениях большое значение имеет рассмотрение различных круговых процессов. Круговым процессом и циклом называется такая последовательность превращений, в результате которой система, выйдя из
какого-либо исходного состояния, вновь в него возвращается.
На диаграмме p – V равновесный круговой процесс изображается замкнутой кривой. Цикл, совершаемый идеальным газом, можно разбить на
процессы расширения (1 – 2) и сжатия (2 – 1) газа. Работа расширения A 1 (опреде-
ляется площадью фигуры 1 a 2 V 2 V 11) положительна (dV > 0), работа сжатия A 2
(определяется площадью фигуры 2 b 1 V 1 V 2 2) отрицательна (dV < 0), Следовательно,
работа, совершаемая газом за цикл, определяется площадью, охватываемой замкну-
той кривой. Если за цикл совершается положительная работа A > 0 (цикл протекает
по часовой стрелке), то он называется прямым (рис. а), если за цикл совершается
отрицательная работа A < 0 (цикл протекает против часовой стрелки), то он называется обратным (рис. б). Прямой цикл используется в тепловых двигателях – периодически действующих двигателях, совершающих работу за счет полученной
извне теплоты. Обратный цик л используется в холодильных машинах – периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой. результате кругового процесса система возвращается в исходное состояние и,
следовательно, полное изменение внутренней энергии газа равно нулю.
Поэтому первое начало термодинамики для кругового процесса 
т. е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и
отдавать, поэтому 
, где Q 1 – количество теплоты, полученное системой;
Q 2 – количество теплоты, отданное системой. Поэтому термический коэффициент
полезного действия для кругового процесса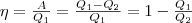 
44 Понятие энтропии впервые введено в 1865 г. Р. Клаузиусом. Для определения физического содержания этого понятия берут отношение теплоты Q, которое получило тело в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.
Приведенное количество теплоты, которое сообщается телу на малом участке процесса, равно δQ/T. Строгий формальный анализ показывает, что приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе, равно нулю:
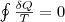(1)
Из равенства нулю интеграла (1), взятого по замкнутому контуру, следует, что подынтегральное выражение δQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, которым система пришла в это состояние. Таким образом,
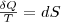(2)
Функция состояния, у которой дифференциал равен δQ/T, называется энтропией и обозначается S.
Из формулы (1) следует, что для обратимых процессов изменение энтропии
(3)
В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:
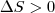(4)
Выражения (3) и (4) применяются только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя произвольным образом. Соотношения (3) и (4) можно представить в виде неравенства Клаузиуса
(5)
т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (2), изменение энтропии
(6)
где подынтегральное выражение и пределы интегрирования определяются через величины, которые характеризуют рассматриваемый процесс. Формула (6) определяет энтропию лишь с точностью до аддитивной постоянной (слагаемого). Физический смысл имеет не сама энтропия, а разность энтропий.
Используя выражение (6), найдем изменение энтропии в процессах идеального газа. Taк как dU=(m/M)CVdT, δA=pdV=(m/M)RT(dV/V), то
или
(7)
т. е. изменение энтропии ΔS1→2 идеального газа при переходе его из cоcтояния 1 в cоcтояние 2 не завиcит от вида процеccа перехода 1→2.
Так как для адиабатического процесса δQ = 0, то ΔS = 0 и, следовательно, S=const, т. е. адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом. Из формулы (7) следует, что при изотермическом процессе (T1= T2)
при изохорном процессе (V1 = V2)
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, которые входят в систему. Свойством аддитивности обладают также внутренняя энергия, масса, объем (но таким свойством не обладают температура и давление).
Более глубокий смысл энтропии показывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, с помощью которых может быть реализовано данное состояние макроскопической системы, или число микросостояний, которые осуществляют данное макросостояние (по определению, W≥1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя ≥1!!!)).
Cогласно Больцману, энтропия cиcтемы и термодинамическая вероятность связаны между собой следующим образом:
(8)
где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть осуществлено данное макросостояние. Значит, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана (8) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. Действительно, чем больше число микросостояний, которые реализуют данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом также максимальна и энтропия.
Так как реальные процессы необратимы, то можно говорить, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, другими словами, от менее вероятных состояний к более вероятным, до тех пор пока вероятность состояния не станет максимальной.
Соотнося выражения (5) и (8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо увеличиваться (в случае необратимых процессов), либо оставаться неизменными (в случае обратимых процессов).
Отметим, однако, что эти утверждения имеют место для систем, которые состоят из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для систем с малым числом частиц могут наблюдаться флуктуации, т. е. энтропия и термодинамическая вероятность состояний замкнутой системы на фиксированном отрезке времени могут уменьшаться, а не увеличиваться, или оставаться постоянными.
45 Первое начало термодинамики, выражая закон cохранения и превращения энергии, не позволяет уcтановить направление протекания термодинамических процеccов. Кроме того, существует множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются. Появление второго начала термодинамики прежде всего связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие нет. Второе начало термодинамики задает направление протекания термодинамических процессов.
Используя понятие энтропии и связанное с ним неравенство Клаузиуса, второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.
Можно дать более короткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Существенен момент, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя произвольным образом (возрастать, убывать, оставаться постоянной). Кроме того, повторим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах и в замкнутой системе энтропия всегда возрастает.
Формула Больцмана S=k•lnW дает объяснение постулируемое вторым началом термодинамики возрастанию энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Значит, формула Больцмана дает статистическое толкование второго начала термодинамики. Являясь статистическим законом, оно описывает закономерности хаотического движения огромного числа частиц, которые составляющих замкнутую систему.
Дадим еще две формулировки второго начала термодинамики:
1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;
2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.
Можно довольно просто доказать эквивалентность формулировок Кельвина и Клаузиуса. Более того, показано, что если в замкнутой системе провести воображаемый процесс, который противоречит второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это же доказывает эквивалентность формулировки Клаузиуса (а значит, и Кельвина) и статистической формулировки, по которой энтропия замкнутой системы не может убывать.
В середине XIX в. возникла проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему и применяя к ней второе качало термодинамики, Клаузиус пришел к утверждению, что энтропия Вселенной когда-нибудь достигнет своего максимума. Это означает, что все формы движения со временем должны перейти в тепловую. При этом переход теплоты от горячих тел к холодным приведет к тому, что температура всех тел во Вселенной станет одинаковой, т. е. наступит полное тепловое равновесие и все процессы во Вселенной остановятся — наступит тепловая смерть Вселенной. Неправильность вывода о тепловой смерти заключается в том, что не имеет смысла применять второе начало термодинамики к незамкнутым системам, например к такой бесконечно развивающейся и безграничной системе, как Вселенная.
Первые два начала термодинамики дают мало сведений о поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом термодинамики, или теоремой Нернста—Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:
Так как энтропия задается с точностью до аддитивной постоянной, то эту постоянную для простоты возьмем равной нулю. При этом отметим, что это произвольное допущение, т.к. энтропия по своей сущности всегда задается с точностью до аддитивной постоянной. Из теоремы Нернста — Планка следует, что теплоемкости Ср и СV при 0 К равны нулю.
46 Цикл Карно представлен на рис. 3, где изотермические расширение и сжатие заданы соответственно кривыми 1—2 и 3—4, а адиабатические расширение и сжатие — кривыми 2—3 и 4—1. U=const при изотермическом процессе, поэтому, используя формулы термодинамики для изопроцессов, количество теплоты Q1, полученное газом от нагревателя, равно работе расширения А12, совершаемой газом при переходе из состояния 1 в состояние 2:
(1)
При адиабатическом расширении 2—3 теплообмен с окружающей средой отсутствует и работа расширения А23 делается за счет изменения внутренней энергии:
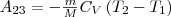
Количество теплоты Q2, которое отдано газом холодильнику при изотермическом сжатии, равно работе сжатия А34:
(2)
Работа адиабатического сжатия
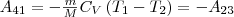
Работа, совершаемая в результате кругового процесса,
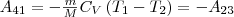
и, как можно показать, определяется площадью, заштрихованной на рис. 87. Термический к. п. д. цикла Карно
Применив формулу TVγ-1=const для адиабатического процесса 2—3 и 4—1, получим
и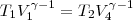 
откуда
(3)
Подставляя (1) и (2) в формулу для КПД для тепловогот процесса и учитывая (3), получаем
(4)
т. е. для цикла Карно КПД действительно определяется только температурами нагревателя и холодильника. Для повышения КПД нужно увеличивать разность температур нагревателя и холодильника. Например, при T1 = 400 К и T2 = 300 К η = 0,25. Если же температуру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то η = 0,5. КПД всякого реального теплового двигателя из-за действыующего трения и неизбежных тепловых потерь гораздо меньше вычисленного для цикла Карно.
Обратный цикл Карно применяется при проектировании тепловых насосов. В отличие от холодильных машин тепловые насосы должны как можно больше тепловой энергии отдавать горячему телу, например системе отопления. Часть этой энергии отбирается от окружающей среды с более низкой температурой, а часть — получается за счет механической работы, производимой, например, компрессором.
Теорема Карно также стала основанием для установления термодинамической шкалы температур.Сравнив левую и правую части формулы (4), получим
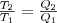(5)
т. е. для сравнения температур Т1 и T2 двух тел необходимо произвести обратимый цикл Карно, в котором одно тело используется как нагреватель, другое как холодильник. Из равенства (5) мы видим, что отношение температур тел равно отношению отданного в этом цикле количества теплоты к полученному. По теореме Карно, химический состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шкала не связана со свойствами какого-то конкретного термометрического тела. Обратим внимание, что таким образом сравнивать температуры практически трудно, так как реальные термодинамические процессы, как уже говорилось, являются необратимыми.