Резонанс напряжений в цепи переменного тока.
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Резонанс напряжений возникает в последовательной RLC-цепи.

От одновременного действия двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.

Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда:
ωL = 1 / ωС.
Цепь в этом случае будет вести себя как чисто активное сопротивление, т. е. как будто в ней нет ни катушки, ни конденсатора. Величина этого сопротивления определится суммой активных сопротивлений катушки и соединительных проводов. При этом действующее значение тока в цепи будет наибольшим и определится формулой закона Ома
I = U / R,
Где вместо Z теперь поставлено R.
Одновременно с этим действующие напряжения как на катушке UL = IXL так и на конденсаторе Uc = IХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений.
Кривые напряжений, тока и мощности при резонансе напряжений в цепи.

Сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ωLвозрастет, а ХС = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему. Такая цепь получила название колебательного контура.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:

Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:


Таким образом, изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
Резонанс токов.
Резонанс токов, параллельный резонанс - получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор вне контура..
Весь контур в целом является нагрузочным сопротивлением для генератора и поэтому генератор

Схема и резонансные кривые для резонанса токов.
включен последовательно, как это и бывает всегда в замкнутой цепи.
Условия получения резонанса токов такие же, как и для резонанса напряжений: f = f0 или xL = хC. Однако по своим свойствам резонанс токов во многом противоположен резонансу напряжений. В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе сопротивление контура между точками разветвления становится максимальным, а ток генератора будет минимальным. Полное (эквивалентное) сопротивление контура для генератора при резонансе токов Rэ можно подсчитать по любой из следующих формул
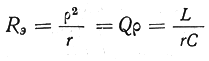 ,
,
где L и С — в генри и фарадах, а Rэ, р и r — в омах.
Сопротивление Rэ, называемое резонансным сопротивлением, является чисто активным и поэтому при резонансе токов нет сдвига фаз между напряжением генератора и его током.
На (рис.1 б) для резонанса токов показано изменение полного сопротивления контура z и тока генератора I при изменении частоты генератора f.
В самом контуре при резонансе происходят сильные колебания и поэтому ток внутри контура во много раз больше, чем ток генератора. Токи в индуктивности и емкости IL и IС можно рассматривать как токи в ветвях или как ток незатухающих колебаний внутри контура, поддерживаемых генератором. По отношению к напряжению U ток в катушке отстает на 90°, а ток в емкости опережает это напряжение на 90°, т. е. друг относительно друга токи сдвинуты по фазе на 180°. Вследствие наличия активного сопротивления, сосредоточенного главным образом в катушке, токи IL, и IC в действительности имеют сдвиг фаз несколько меньше 180° и ток IL немного(меньше IC. Поэтому по первому закону Кирхгофа для точки разветвления можно написать

Чем меньше активное сопротивление в контуре, тем меньше разница между IC и IL, тем меньше ток генератора и тем больше сопротивление контура. Ток, идущий от генератора, пополняет энергию в контуре, компенсируя потери ее в активном сопротивлении. При уменьшении активного сопротивления уменьшается потеря энергии в нем и генератор расходует меньше энергии на поддержание незатухающих колебаний.
Если бы контур был идеальным, то начавшиеся колебания продолжались бы непрерывно без затухания и не требовалось бы энергии от генератора на их поддержание. Ток генератора был бы равен нулю, а сопротивление контура — бесконечности.

Активная мощность, расходуемая генератором, может быть подсчитана как

или как мощность потерь в активном сопротивлении контура

где Iк — ток в контуре, равный IL или IC.