Определение момента инерции маятника Максвелла.
Цель работы: используя закон сохранения энергии определить момент инерции кольца по результатам эксперимента и сравнить полученные результаты с теоретическими значениями.
Приборы: 1. Маятник Максвелла FPM–03.
2. Набор колец (4шт.).
Краткая теория.
Энергия вращающегося абсолютно твердого тела (а.т.т.).
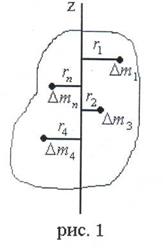
Рассмотрим а.т.т. вращающееся вокруг произвольной неподвижной оси Z. Мысленно разобьем все тело массой m на элементарные массы ∆mi (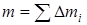
), находящиеся, соответственно, на расстояниях ri от оси вращения (рис.1).
|
При вращении тела, элементарные массы будут описывать окружности различных радиусов. Кинетическая энергия (Wki) каждой элементарной массы определится по формуле (1):
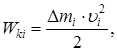
| (1) |
где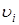 
– линейная скорость i – ой элементарной массы.
Линейная скорость
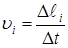
определяется длиной дуги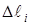 
, которую будет описывать каждая частица за время 
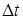, а т.к. длина дуги частиц зависит от расстояния 
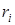до оси вращения, то линейные скорости 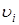будут различны, но одинаковы угловые скорости
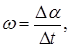
где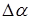 
- угловое перемещение.
Используя формулу связи угловой и линейной скорости
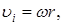
выразим кинетическую энергию элементарной массы через угловую скорость
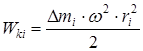
| (2) |
Кинетическая энергия всего твердого тела, будет равна сумме кинетических энергий элементарных масс (3).
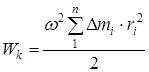
| (3) |
Сумма произведений элементарных масс на квадрат расстояния их до оси вращения называется моментом инерции тала – J (4).
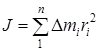
| (4) |
Момент инерции тела характеризует массу тела с учетом распределения элементарных масс в пространстве (формы тела) относительно оси вращения.
Подставляя формулу (4) в (3) получим окончательное выражение для кинетической энергии тела, вращающегося вокруг неподвижной оси:
|
|
 .
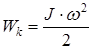| (5) |
Если, вращающееся а.т.т. одновременно перемещается в пространстве, то такое движение тела можно представить как сумму поступательного движения центра масс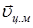 
и вращательного движения с угловой скоростью 
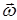около мгновенной оси вращения, проходящей через центр масс. Абсолютная скорость частиц 
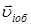будет складываться из скорости движения центра масс и относительной скорости вращения частиц
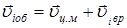, но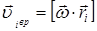 
Таким образом:
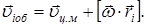
| (6) |
Подставляя равенство (6) в уравнение (1) и суммируя элементарные массы, получим:
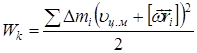
| (7) |
Преобразуем уравнение (7):
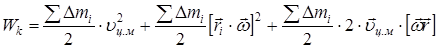
| (8) |
В формуле (8) первое слагаемое определяет кинетическую энергию поступательно движущегося а.т.т.:
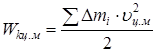
| (9) |
Второе слагаемое – кинетическую энергию а.т.т., вращающегося вокруг оси, проходящей через центр масс:
 
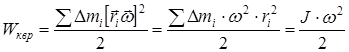
| (10) |
Третье слагаемое перепишем в виде:
.
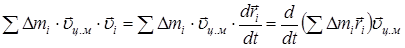Если ось вращения проходит через центр масс, то для центра масс сумма,
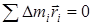
| (11) |
и третье слагаемое будет равно нулю.
Учитывая формулы (8 – 11), получим:
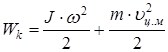
| (12) |
Кинетическая энергия а.т.т., движущегося поступательно и вращающегося вокруг оси, проходящей через центр масс, равна кинетической энергии тела, вращающегося вокруг оси, проходящей через центр масс плюс кинетическая энергия поступательного движения тела.
Если тело движется в силовом поле, то оно обладает и потенциальной энергией. Тогда полная энергия тела
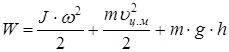
и по закону сохранения энергии, она является постоянной величиной.