1. Пункт плана 1 выполнить самостоятельно.
2. Уровни и интервалы варьирования факторов, а также формулы перевода натуральных х 1, х 2 в нормированные Х 1, Х 2 и обратно, приведены в таблице 2 (см. уравнения (2) – (5))
Таблица 2. – Уровни и интервалы варьирования факторов
| Факторы | 1-й фактор (семена) | 2-й фактор (удобрение) | ||
| x 1, ц/га | X 1 | x 2, ц/га | X 2 | |
| Нижний уровень | x 1 min = 2 | ‑1 | x 2 min = 1 | ‑1 |
| Верхний уровень | x 1 max = 5 | +1 | x 2 max = 2 | +1 |
| Основной уровень | x 10 = 3.5 | x 20 = 1.5 | ||
| Интервал варьирования | D x 1 = 1.5 | D x 2 = 0. 5 | ||
| Формулы перевода натуральных (х 1, х 2) в нормированные (Х 1 Х 2) r и обратно |  ;  ;
 ;  .
|
3. В качестве матрицы планирования (таблица 3) для построения двухфакторного уравнения регрессии первого порядка 
возьмем ЦПФП с числом опытов 
(
) и числом дублей 
(см. радел А, п. 3).
3.1. Методика эксперимента. Так как общее количество опытов 
и число дублей , организуем в теплице 20 делянок площадью по 1 м2. Количество посевного материала и неорганического удобрения вносится в каждую делянку согласно ЦПФП. Все остальные факторы (количество воды, света, тепла, сроки посева и сбора) поддерживаются на фиксированных, одинаковых для всех делянок уровнях. Полученные результаты эксперимента из таблицы 1 перенесём в таблицу 3.
Таблица 3. – Матрица планирования на базе ЦПФП для 
,
и результаты предварительной обработки экспериментальных данных.
| N 2 | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
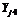
| – | – | 45.00 | 0.6667 | |||||||
| + | – | 36.00 | 2.000 | |||||||
| – | + | 57.00 | 2.000 | |||||||
| + | + | 49.50 | 1.667 | |||||||
| 3.5 | 1.5 | 54.00 | 2.000 | |||||||
| 
| 
| 
|
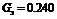
3.2. Выполним предварительную обработку экспериментальных данных (внести в таблицу 3).
Выборочное среднее в каждом опыте (см. уравнение (6)):
, 
.
Например, выборочное среднее в опыте № 2:
.
Выборочная дисперсия в каждом опыте (см. уравнение (7)):
, .
Например, выборочное среднее в опыте № 2:
.
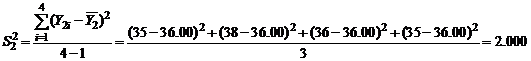Проверка выборочных дисперсий на однородность по критерию Кохрена:
‑ экспериментальное значение критерия Кохрена (см. уравнение (8)):
,
‑ критическое значение критерия Кохрена 
при числах степеней свободы 
, 
и доверительной вероятности р выбирается из таблицы Приложения 5:
.
Вывод: выборочные дисперсии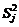 
однородны, так как 
(см. уравнение (9)).
Так как все выборочные дисперсии однородны, рассчитаем дисперсию воспроизводимости и её число степеней свободы 
(см. уравнения (11) – (12)):
,
.
4. Создадим матрицу моделирования для построения двухфакторного уравнениярегрессии первого порядка на базе ЦПФП (таблица 4) (раздел А, п. 5).
Таблица 4. ‑ Матрица моделирования для построения двухфакторного
уравнениярегрессии первого порядка на базе ЦПФП.
| N | 
|
|
| 
| 
| 
| 
| 
| 
|
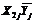
| + | ‑ | ‑ | 45.00 | +45.00 | –45.00 | –45.00 | 46.00 | 1.000 | |
| + | + | ‑ | 36.00 | +36.00 | +36.00 | –36.00 | 37.80 | 3.240 | |
| + | ‑ | + | 57.00 | +57.00 | –57.00 | +57.00 | 58.80 | 3.240 | |
| + | + | + | 49.50 | +49.50 | +49.50 | +49.50 | 50.60 | 1.210 | |
| + | 54.00 | +54.00 | 0×54.00 | 0×54.00 | 48.30 | 32.49 | |||
| 
| 241.5 | –16.50 | 25.50 | j = 41.18 | ||||
| 
| 48.30 | ‑4.125 | 6.375 | 
| ||||
| Уравнение неадекватно | 
| 0.9 | 1.0 | 1.0 |
4.1. Рассчитаем коэффициенты двухфакторного уравнениярегрессии первого порядка (результаты расчета внесем в таблицу 4):
Создадим столбцы 
и рассчитаем суммы 
, 
:
;
;
.
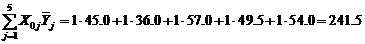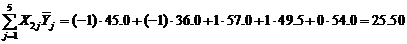Рассчитаем суммы 
:
;
.
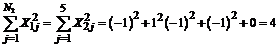Рассчитаем коэффициенты регрессии (см. уравнение (13) – (16)):
;
; 
.
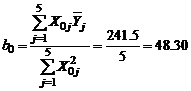4.2. Проверим коэффициенты b 0, b 1, b 2 на значимость по критерию Стьюдента.
Рассчитаем дисперсии значимости 
(см. уравнения (17) – (19):
; 
;
; 
.
Рассчитаем доверительные интервалы 
(см. уравнение (20) – (21)):
,
,
где 
– табличное значение критерия Стьюдента при числе степеней свободы 
и доверительной вероятности р = 0.95 выбираем из таблицы Приложения 2:
С учетом доверительных интервалов корректно запишем значения коэффициентов 
:
,
,
.
Вывод: все три регрессионных коэффициента 
значимы, так как (см. уравнение (23)):
, 
, 
.
Таким образом, двухфакторное уравнение регрессии первого порядка, в котором все три регрессионных коэффициента значимы, имеет следующий вид:
.
4.3. Проверим полученное двухфакторное уравнение регрессии первого порядка на адекватность по критерию Фишера (результаты расчета внесем в таблицу 4):
Рассчитаем параметр 
в каждом опыте по двухфакторному уравнению регрессии первого порядка. Например: 
.
Образуем столбец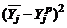 
, и рассчитаем его значения. Например:
.
Рассчитаем остаточную сумму квадратов
;
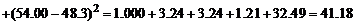Рассчитаем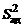 
и её число степеней свободы 
(см. уравнения (24) – (25)):
; 
.
Проверим полученное двухфакторное уравнение регрессии на адекватность по критерию Фишера:
‑ экспериментальное значение критерия Фишера 
(см. уравнение (26)):
, так как 
;
‑ табличное значение критерия Фишера 
при числах степеней свободы 
, 
и доверительной вероятности р = 0.95 выбираем из таблицы Приложения 4: 
.
Вывод: полученное двухфакторное уравнение регрессии первого порядка неадекватно, так как 
(см. уравнение (28)).
5. Так как полученное уравнение регрессии первого порядка неадекватно, следует перейти к построению двухфакторного ортогонализированного уравнения второго порядка.
План решения типовой задачи (уравнение регрессии второго порядка)
1. Создать матрицу планирования для построения ортогонализированного двухфакторного уравнениярегрессии второго порядка на базе ОЦКП и выполнить предварительную обработку экспериментальных данных.
2. Создать матрицу моделирования для построения ортогонализированного двухфакторного уравнениерегрессии второго порядка, рассчитать коэффициенты 
и произвести статистическую оценку качества полученногоуравнениярегрессии(значимость коэффициентов регрессии, адекватность уравнения регрессии).
3. Найти оптимальные значения факторов, при которых параметр Y достигает максимальной величины, а также её абсолютную и относительную погрешность.
4. Принять решение о дальнейшем пути исследования изучаемого объекта.
Дополнительные экспериментальные данные по урожайности пшеницы (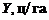
) на базе ОЦКП с числом опытов 
и числом дублей для звёздных опытов (№№ 6 – 9) представлены в таблице 5.
Таблица 5. ‑ Экспериментальные данные для звёздных точек ОЦКП
| N 2 |
|
|
|
|
|
|
| – | ||||||
| + | ||||||
| ‑ | ||||||
| + |
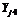
Решение задачи по плану
1. Создадим матрицу планирования (таблица 6) (см. раздел Б, п. 9), дополнив матрицу планирования (таблица 3) звездными точками 
. Для 
(см. уравнение (30)). Количество опытов ОЦКП равно 
, количество дублей . Внесём в матрицу планирования (таблица 6) экспериментальные данные из таблицы2и дополнительные экспериментальные данные для звёздных опытов из таблицы 5.
Таблица 6. ‑ Матрица планирования на базе ОЦКП для k = 2 и
результаты предварительной обработки
| N |
|
|
|
|
|
|
|
|
|
|
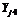
| ‑ | – | 45.00 | 0.6667 | |||||||
| + | – | 36.00 | 2.000 | |||||||
| ‑ | + | 57.00 | 2.000 | |||||||
| + | + | 49.50 | 1.667 | |||||||
| 54.00 | 2.000 | |||||||||
| ‑ | 57.00 | 0.6667 | ||||||||
| + | 49.50 | 1.6667 | ||||||||
| – | 43.00 | 6.000 | ||||||||
| + | 56.50 | 1.667 | ||||||||
| 
| 
| 
|
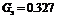
1.1. Выполним предварительную обработку экспериментальных данных, результаты расчета внесем в таблицу 6.
Выборочное среднее в звездных точках (см. уравнение (6)):
, 
.
Например, выборочное среднее в опыте № 8:
.
Выборочная дисперсия в звездных точках (см. уравнение (7)):
, .
Например, выборочное среднее в опыте № 8:
Проверка выборочных дисперсий на однородность по критерию Кохрена:
‑ экспериментальное значение критерия Кохрена (см. уравнение (8)):
,
‑ критическое значение критерия Кохрена при числах степеней свободы , и доверительной вероятности р выбирается из таблицы Приложения 5: 
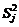. Вывод: 9 выборочных дисперсий однородны, так как 
. (см. уравнение (9)).
1.2. Так как все выборочные дисперсии однородны, рассчитаем дисперсию воспроизводимости и её число степеней свободы (см. уравнение (11) – (12)):
, 
.
2. Создадим матрицу моделирования на базе матрицы ОЦКПдля построения ортогонализированного двухфакторного уравнениерегрессии второго порядка 
(таблица 7). Создадим столбцы N 2, 
, где ортогонализирующий коэффициент 
(см. уравнение (32))и внесем в матрицу моделирования выборочные средние каждого опыта из таблицы 6.
Таблица 7. ‑ Матрица моделирования для построения ортогонализированного
двухфакторного уравнениярегрессии второго порядка на базе ОЦКП.
| N k |
|
|
| 
| 
| 
|
|
|
|
| 
| 
|
|
|
|
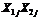
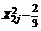
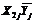
| + | ‑ | ‑ | + | 1/3 | 1/3 | 45.00 | +45.00 | ‑ 45.00 | ‑ 45.00 | +45.00 | 1/3×45.00 | 1/3×45.00 | 44.59 | 0.1681 | |
| + | + | + | – | 1/3 | 1/3 | 36.00 | +36.00 | +36.00 | ‑ 36.00 | ‑ 36.00 | 1/3×36.00 | 1/3×36.00 | 36.59 | 0.3481 | |
| + | ‑ | ‑ | – | 1/3 | 1/3 | 57.00 | +57.00 | ‑ 57.00 | +57.00 | ‑ 57.00 | 1/3×57.00 | 1/3×57.00 | 57.59 | 0.3481 | |
| + | + | + | + | 1/3 | 1/3 | 49.50 | +49.50 | +49.50 | +49.50 | +49.50 | 1/3×49.50 | 1/3×49.50 | 49.59 | 0.0081 | |
| + | ‑ 2/3 | ‑ 2/3 | 54.00 | +54.00 | 0×54.00 | 0×54.00 | 0×54.00 | ‑ 2/3×54.00 | ‑ 2/3×54.00 | 54.99 | 0.9801 | ||||
| + | ‑ | 1/3 | ‑ 2/3 | 57.00 | +57.00 | ‑ 57.00 | 0×57.00 | 0×57.00 | 1/3×57.00 | ‑ 2/3×57.00 | 56.79 | 0.0441 | |||
| + | + | 1/3 | ‑ 2/3 | 49.50 | +49.50 | +49.50 | 0×49.50 | 0×49.50 | 1/3×49.50 | ‑ 2/3×49.50 | 48.79 | 0.5041 | |||
| + | ‑ | ‑ 2/3 | 1/3 | 43.00 | +43.00 | 0×43.00 | ‑ 43.00 | 0×43.00 | ‑ 2/3×43.00 | 1/3×43.00 | 42.79 | 0.0441 | |||
| + | + | ‑ 2/3 | 1/3 | 57.50 | +57.50 | 0×57.50 | +57.50 | 0×57.50 | ‑ 2/3×57.50 | 1/3×57.50 | 55.79 | 0.5041 | |||
|
|
| 447.5 | ‑ 24.00 | 39.00 | 1.500 | ‑ 4.333 | ‑ 11.33 | j = 2.949 | |||||||
|
| 49.72 | ‑ 4.000 | 6.500 | 0.3750 | ‑ 2.167 | ‑ 5.665 | 
| |||||||
| Уравнение адекватно |
| 0.49 | 0.6 | 0.6 | 0.7 | 1.0 | 1.0 |
2.1. Рассчитаем коэффициенты ортогонализированного двухфакторного уравнения регрессии второго порядка 
(значения 
тоже изменятся, так как число опытов увеличилось с 5-ти до 9-ти).
Создадим столбцы 
и рассчитаем суммы 
, 
(результаты расчета внести в таблицу 6).
;
;
;
;
;
.
Рассчитаем суммы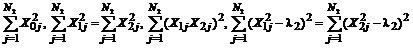 
:
;
;
;
.
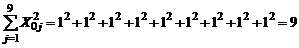2.2. Рассчитаем коэффициенты двухфакторного ортогонализированного уравнения регрессии второго порядка (см. уравнения (33) – (36)):
;
; 
;
;
; 
.
2.3. Проверим полученные коэффициенты ортогонализированного двухфакторного уравнения регрессии второго порядка на значимость.
Рассчитаем дисперсии значимости коэффициентов ортогонализированного двухфакторного уравнения регрессии второго порядка (см. уравнения (37) – (43)):
;
;
;
.
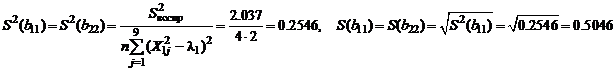Рассчитаем доверительные интервалы коэффициентов ортогонализированного двухфакторного уравнения регрессии второго порядка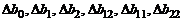 
по критерию Стьюдента (см. уравнения (44) – (50)):
;
;
;
.
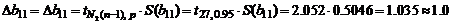где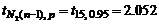 
– табличное значение критерия Стьюдента при числе степеней свободы 
и доверительной вероятности р = 0.95 выбираем из таблицы Приложения 2:
Корректно запишем значения коэффициентов 
:
,
, 
,
,
, 
.
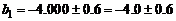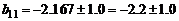Регрессионные коэффициента 
значимы, так как (см. уравнения (51) – (54)):
;
, 
.
, 
Регрессионный коэффициент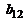 
незначим, так как 
.
Вывод: ортогонализированное двухфакторное уравнение регрессии второго порядка, в котором 5 коэффициентов 
значимы, а коэффициент 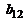незначим, имеет следующий вид:
.
2.4. Проверим полученное ортогонализированное двухфакторное уравнение регрессии второго порядка на адекватность по критерию Фишера:
Рассчитаем параметр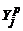 
по ортогонализированному двухфакторному уравнению регрессии второго порядка в каждом опыте (результаты расчета внести в таблицу 6). Например:
.
Образуем столбец 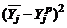и рассчитаем его значения (результаты расчета внести в таблицу 6), например: 
.
Рассчитаем остаточную сумму квадратов 
:
Рассчитаем дисперсию адекватности 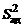и её число степеней свободы (см. уравнения (55)–(56)):
, 
,
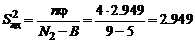где В – число значимых коэффициентов ортогонализированного двухфакторного уравнения регрессии второго порядка. В данной задаче 
.
Проверим полученное ортогонализированное двухфакторное уравнение регрессии второго порядка на адекватность по критерию Фишера:
‑ экспериментальное значение критерия Фишера (см. уравнения (26)):
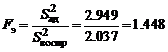, так как ;
‑ критическое значение критерия Фишера при числах степеней свободы 
, 
и доверительной вероятности р = 0.95 выбираем из таблицы Приложения 4: 
.
Вывод: полученное двухфакторное ортогонализированное уравнение регрессии второго порядка
.
адекватно, так как 
(см. уравнения (27)).
3. Рассчитаем оптимальные нормированные 
и натуральные 
значения факторов, при которых параметр Y (Х 1, X 2) достигает максимума. Так как коэффициенты регрессии 
и 
, а 
незначим (см. уравнения (58)), то нормированные значения равны:
; 
.
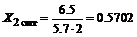Оптимальные значения факторов в натуральных координатах 
, 
равны (см. уравнение (3)):
;
.
3.1. Рассчитаем максимальную урожайность пшеницы 
по адекватному ортогонализированному многофакторному уравнению регрессии второго порядка:
.
3.2. Рассчитаем абсолютную 
и относительную погрешность 
параметра Y max, рассчитанного по адекватному ортогонализированному двухфакторному уравнению регрессии второго порядка 
(см. уравнение (58)):
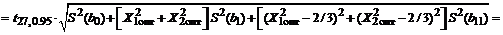
‑ относительная погрешность :
;
С учетом абсолютной погрешности 
корректно запишем :
, ц/га
4. Основной вывод: максимальная урожайность пшеницы 
может быть достигнута при внесении в почву х 1 = 2.1 ц/га семян и х 2 = 1.8 ц/га неорганического удобрения.