Тема: «Иррациональные уравнения и неравенства»
Теоретический блок
Задание 1: Изучить теоретический материал и составить конспект темы по вопросам:
1)Уравнения с одним неизвестным, равносильность уравнений. Общие методы решения уравнений. Линейные, квадратные, биквадратные, приводящиеся к квадратным, рациональные, иррациональные уравнения.
2) Основные методы решения иррациональных уравнений (на конкретных примерах)
3)Неравенства с одним неизвестным, свойства числовых неравенств Линейные неравенства, неравенства с модулем. Квадратные неравенства, Рациональные и иррациональные неравенства. Системы и совокупности неравенств.
4) Методика решения иррациональных неравенств (на конкретных примерах)
5) Тождественные преобразования при решении иррациональных уравнений и неравенств
Методические указания
Перед выполнением теоретического блока следует внимательно изучить задания, подобрать необходимый материал, воспользоваться списком рекомендованной литературы. При необходимости нужно использовать справочники и другие доступные источники информации. Обязательно необходимо указать все данные источника (автор, название, год выпуска, издательство, название сайта, электронный адрес).
Отчёт по теоретическому блоку работы следует оформлять придерживаясь следующего последовательности: основные понятия, определения, рисунки, схемы, формулы, теоремы (желательно с доказательством) и следующего содержания: введение, основная часть, примеры с решениями (объяснениями), заключение, список используемой литературы. Титульный лист выполненной самостоятельной работы следует напечатать по образцу (Приложение № 1).
Рекомендуемая литература:
1. Богомолов Н.В.,Самойленко П.И. Математика. –М.:Дрофа,2009.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 10-е изд. – М.: Высшая школа, 2008.
3. Валуцэ И.И. Математика для техникумов. - М.: Наука,2008.
4. Выгодский М.Я. Справочник по высшей математике. – М.: Рост книга, 2009.
5. С.Г. Григорьев, С.В.Задулина. Математика.-М.: АСАDEMA,2008.
6. Дадаян А.А. Сборник задач по математике.-М.: ФОРУМ-ИНФРА-М,2009.
7. Дадаян А.А. Математика.-М.: ФОРУМ-ИНФРА-М,2009.
8. INTERNET
Теоретический блок является основой для выполнения практического блока.
Практический блок
Задание 2: Решить следующие задачи:
Задача № 1: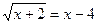 
Задача № 2: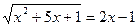 
Задача № 3: 
Задача № 4: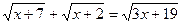 
Задача № 5: 
Задача № 6: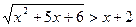 
Задача № 7: 
Задача № 8: 
Методические указания
Для выполнения данного задания внимательно изучите приведенные ниже примеры с подробными решениями, а затем выполните аналогичные практические задания.
Пример 1. Решите уравнение 
.
Решение. Возведем обе части этого уравнения в квадрат 
и получим 
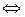
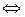
, откуда следует, что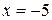 
или 
. Проверка. :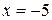 
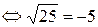. Это неверное числовое равенство, значит, число 
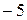не является корнем данного уравнения. : 
. Это верное числовое равенство, значит, число 
является корнем данного уравнения.
Ответ. .
Пример 2. Решить уравнение 
.
Решение. Это уравнение равносильно системе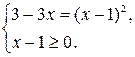 
Решая первое уравнение этой системы, равносильное уравнению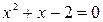 
, получим корни 
и 
.
Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения.
Ответ. 
.
Пример 3. Решить уравнение 
Решение. Метод уединения радикала приводит к уравнению 
. Это уравнение равносильно системе
Решая первое уравнение этой системы, получим корни 
и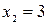 
, но условие 
выполняется только для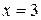 
.
Ответ. .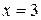
Пример 4. Решить уравнение
.
Решение. Это уравнение равносильно системе
Решая первое уравнение этой системы, равносильное уравнению 
, получим корни 
и 
.
Однако при этих значениях x не выполняется неравенство 
, и потому данное уравнение не имеет корней.
Ответ. Корней нет.
Пример 5. Решить уравнение 
.
Решение. Возведем обе части уравнения в квадрат и произведем приведение подобных членов, перенос слагаемых из одной части равенства в другую и умножение обеих частей на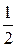 
. В результате получим уравнение
,
(1)являющееся следствием исходного.
Снова возведем обе части уравнения в квадрат. Получим уравнение
,которое приводится к виду 
.
Это уравнение (также являющееся следствием исходного) имеет корни 
, 
. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ. , .
Методика решения иррациональных неравенств
Иррациональное неравенство 
(или 
) равносильно системе неравенств
или 
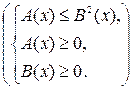. {1}
Иррациональное неравенство 
(или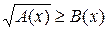 
) равносильно совокупности двух систем неравенств
или 
. {2}
Иррациональное неравенство 
(или 
) равносильно системе неравенств
или 
. {3}
Пример 1. Решить неравенство 
.
Решение. Заметим, что правая часто этого неравенства отрицательна, в то время как левая часть неотрицательна при всех значениях x, при которых она определена. Поэтому неравенство решений не имеет.
Ответ. Решений нет.
Пример 2. Решить неравенство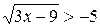 
.
Решение. Как и в предыдущем примере, заметим, что правая часть данного неравенства отрицательна, следовательно, возводить это неравенство в квадрат нельзя. И не надо, поскольку левая часть исходного неравенства неотрицательна при всех значениях x, при которых она определена. Это означает, что левая часть больше правой части при всех значениях x, удовлетворяющих условию 
.
Ответ. 
.
Пример 3. Решить неравенство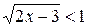 
.
Решение. В соответствии со схемой {1} решения неравенств этого типа, запишем равносильную ему систему рациональных неравенств
Условие 
выполнено при всех x, и нет необходимости добавлять его к выписанной системе.
Ответ. 
.
Пример 4. Решить неравенство 
.
Решение. Это неравенство решается при помощи схемы {2}. В данном случае 
, поэтому можно сразу записать неравенство, равносильное исходному 
. Ответ. 
.
Пример 5. Решить неравенство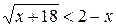 
.
Решение. Это неравенство может быть решено при помощи схемы {1}. Система, равносильная исходному неравенству, имеет вид 
Ответ.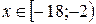 
.
Пример 6. Решить неравенство 
.
Решение. Данное неравенство можно решать с помощью схемы {2}. Оно равносильно совокупности двух систем
Ответ. 
.
Пример 7. Решить неравенство 
.
Решение. Согласно схеме {3}, данное неравенство равносильно системе
Ответ.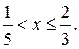 
Рекомендуемая литература:
1. Богомолов Н.В.,Самойленко П.И. Математика. –М.:Дрофа,2009.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 10-е изд. – М.: Высшая школа, 2008.
3. Валуцэ И.И. Математика для техникумов. - М.: Наука,2008.
4. Выгодский М.Я. Справочник по высшей математике. – М.: Рост книга, 2009.
5. С.Г. Григорьев, С.В.Задулина. Математика.-М.: АСАDEMA,2008.
6. Дадаян А.А. Сборник задач по математике.-М.: ФОРУМ-ИНФРА-М,2009.
7. Дадаян А.А. Математика.-М.: ФОРУМ-ИНФРА-М,2009.
8. INTERNET
Форма отчетности
Выполненную самостоятельную работу оформить по одному из трёх вариантов:
Напечатать в программе MICROSOFT WORD (кегль - 14, интервал -1,5; шрифт - Times New Roman; поля – 1,2,1,1; нумерация страниц). Сохранить файл под своей фамилией и сдать электронную версию преподавателю на носителе. Распечатать на листах формата А4.