В рамках данной работы сначала следует подробнее рассмотреть теоретические аспекты машины Тьюринга, а затем разобрать основы морфологического разбора предложения.
Алан Тьюринг (1912–1954) – английский математик. Он дал определение алгоритма через построение, названное машиной Тьюринга. В 1936 году Тьюринг предложил определение вычислимости, которое основано на анализе осуществления алгоритма человеком, располагающим ручкой для письма и бумагой. Он рассматривает это как последовательность очень простых действий следующего вида:
(a) – запись или стирание одного символа;
(b) – перенесение внимания с одного участка бумаги на другой.
На каждом шаге алгоритм определяет действие, которое будет совершено на следующем шаге. Это зависит только от (i) символа на участке бумаги, который обозревается в данный момент глазом (или другим рецептором) и (ii) текущим состоянием (мысли) человека. Чтобы обеспечить возможность реализации алгоритма, мы предполагаем, что это состояние полностью определяется самим алгоритмом и предысторией его работы. Оно может включать частичную запись того, что произошло до сих пор, но не зависит от настроения или сообразительности исполнителя алгоритма или от его самочувствия. Кроме того, существует только конечное число различимых состояний, в которых может находиться исполнитель, так как он конечен в рассматриваемых аспектах. Состояние исполнителя может, конечно, изменяться в результате действия, предпринятого на этом шаге.
Тьюринг изобрёл конечные машины, которые выполняют алгоритмы, представленные таким способом. Для каждого алгоритма существует своя, хотя и не единственная, машина. Рассмотрим кратко эти машины.
Итак, машина Тьюринга – это конечное устройство, которое производит действия на бумажной ленте.
В состав Машины Тьюринга входит бесконечная в обе стороны лента, разделённая на ячейки (лента представляет собой бумагу, которая требуется исполнителю для осуществления алгоритма; каждый квадрат представляет собой порцию ленты, обозреваемую в данный момент) и управляющее устройство, способное находится в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано. В каждой ячейке может быть записан некоторый символ из фиксированного (для данной машины) конечного множества, называемого алфавитом данной машины. Один из символов алфавита выделен и называется «пробелом» (s0) предполагается, что изначально вся лента пуста, то есть, заполнена пробелами.
Машина Тьюринга может менять содержимое ленты с помощью специальной читающей и пишущей головки, которая движется вдоль ленты. В каждый момент головка находится в одной из ячеек. Машина Тьюринга получает от головки информацию о том, какой символ та видит, и в зависимости от этого (и от своего внутреннего состояния) решает, что делать, то есть какой символ записать в текущей ячейке и куда сдвинуться после этого (налево, направо или остаться на месте). При этом также меняется внутреннее состояние машины (мы предполагаем, что машина не считая ленты, имеет конечную память, то есть конечное число внутренних состояний).
Таким образом, чтобы задать машину Тьюринга, надо указать следующие объекты:
· произвольное конечное множество A (алфавит); его элементы называются символами;
· некоторый выделенный символ a0  A (пробел, или пустой символ);
A (пробел, или пустой символ);
· конечное множество S, называемое множеством состояний;
· некоторое выделенное состояние s0  S, называемое начальным;
S, называемое начальным;
· таблицу переходов, которая определяет поведение машины в зависимости от состояния и текущего символа;
· некоторое подмножество F  S, элементы которого называются заключительными состояниями (попав в такое состояние, машина останавливается).
S, элементы которого называются заключительными состояниями (попав в такое состояние, машина останавливается).
Таблица переходов устроена следующим образом: для каждой пары (текущее состояние, текущий символ) указана тройка (новое состояние, новый символ, сдвиг) Здесь сдвиг одно из чисел -1 (влево), 0 (на месте) и 1 (направо). Таким образом, таблица переходов есть функция типа:
S x A → S x A x {-1,0,1},
определенная на тех парах, в которых состояние не является заключительным.
Остается описать поведение машины Тьюринга. В каждый момент имеется некоторая конфигурация, складывающаяся из содержимого ленты (формально говоря, содержимое ленты есть произвольное отображение Z → A), текущей позиции головки (некоторое целое число) и текущего состояния машины (элемент S). Преобразование конфигурации в следующую происходит по естественным правилам: мы смотрим в таблице, что надо делать для данного состояния и для данного символа, то есть, выясняем новое состояние машины, меняем символ на указанный и после этого сдвигаем головку влево, вправо или оставляем на месте. При этом если новое состояние является одним из заключительных, работа машины заканчивается. Остается договориться, как мы подаем информацию на вход машины и, что считается результатом ее работы. Будем считать, что алфавит машины, помимо пробела, содержит символы 0 и 1 (а также, возможно, еще какие-то символы). Входом и выходом машины будут конечные последовательности нулей и единиц (двоичные слова). Входное слово записывается на пустой ленте, головка машины ставится в его первую клетку, машина приводится в начальное состояние и запускается. Если машина останавливается, результатом считается двоичное слово, которое можно прочесть, начиная с позиции головки и двигаясь направо (пока не появится символ, отличный от 0 и 1).
Таким образом, любая машина Тьюринга задает некоторую частичную функцию на двоичных словах. Все такие функции естественно назвать вычислимыми на машинах Тьюринга.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила, и недетерминированной в противном случае.
Интуитивное понимание:
Интуитивное понимание машины Тьюринга таково: имеется бесконечная лента, разделённая на клетки. По клеткам ездит каретка. Прочитав букву, записанную в клетке, каретка движется вправо, влево или остаётся на месте, при этом буква заменяется новой. Некоторые буквы останавливают каретку и завершают работу.
Полнота по Тьюрингу:
Можно сказать, что Машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий. Элементарность действий заключается в том, что действие меняет лишь небольшой кусочек данных в памяти (в случае Машины Тьюринга – лишь одну ячейку), и число возможных действий конечно. Несмотря на простоту машины Тьюринга на ней можно вычислить все, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой.
Пример машины Тьюринга:
Приведем пример МТ для умножения чисел в унарной системе счисления. Машина работает по набору правил, приведённых в таблице 1:
Таблица 1. Набор правил
| Набор правил | Набор правил |
| q0*→q0R | q4a→q4aR |
| q01→q0R | q4=→q4=R |
| q0×→q1×R | q41→q41R |
| q11→q2aR | q4*→q51R |
| q21→q21L | q5^→q2*L |
| q2a→q2aL | q6a→q61R |
| q2=→q2=L | q6×→q7×R |
| q2×→q3×L | q7a→q7aR |
| q31 → q4aR | q71→q2aR |
| q3a→q3aL | q7=→q8=L |
| q3*→q6*R | q8a→q81L |
| q4×→q4×R | q8×→q9H |
Конкретная машина Тьюринга задается перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо(R), остаться на месте(H)). Для каждой возможной конфигурации <qi, aj> имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.
Классификация машин Тьюринга:
Существуют различные модификации и обобщения машины Тьюринга; к ним относятся, в частности, многоленточные и многоголовочные машины, а также машины с различными ограничениями возможностей передвижения головки и преобразования информации на ленте.
Попытка классификации машин Тьюринга, предпринята В.А. Успенским и А.Л. Семеновым [1987, с. 238–243]. Следуя ей, изобразим следующую классификационную схему:

Рассмотрим подробнее многоленточную машину Тьюринга: многоленточные машины Тьюринга имеют несколько (конечное множество) лент, каждая со своей головкой, управляющему устройству доступны символы, находящиеся в ячейках, на которых расположены головки лент. Выделены две ленты: входная, с которой разрешается только читать символы, и выходная, на которую разрешается только писать символы. Остальные ленты называются рабочими. Многоленточная машина называется k-ленточной, если у нее k рабочих лент. Действие за такт работы состоит в изменении состояния управляющего устройства, изменении символов в ячейках под головками и изменении положений головок на лентах (каждая головка сдвигается не более чем на одну позицию). Это действие однозначно определяется состоянием управляющего устройства и набором символов в ячейках под головками. Если действие выполнить нельзя, машина останавливается.
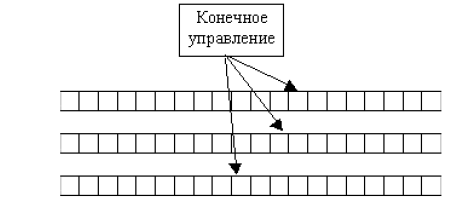
При одном движении, зависящем от состояния конечного управления и сканируемого символа каждой из ленточных головок, машина может:
1) изменить состояние;
2) напечатать новый символ на каждой из сканируемых ячеек;
3) передвинуть каждую из ее ленточных головок независимо друг от друга на одну ячейку влево, вправо или оставить ее на том же месте.
Сначала входная цепочка имеется только на первой ленте, а все другие ленты пусты.
Таким образом, мы определились, что машина Тьринга – это конечное устройство, которое производит действия на бумажной ленте. Также мы рассмотрели классификацию машин Тьюринга, принцип работы, а также состав и назначение машины Тьюринга.
Теперь рассмотрим основы морфологического разбора предложения. Для начала определимся, что же такое морфология, а затем подробно рассмотрим все тонкости данного разбора.
Итак, морфология – это раздел науки о языке, который изучает части речи. Все слова русского языка объединены в группы, которые называются частями речи – это лексико-грамматические классы слов, в которых слова объединяются на основе следующих критериев:
1. Общего грамматического значения (предмета, признака предмета, количества и так далее)
2. Одинакового набора постоянных морфологических признаков (например, для существительных – собственное или нарицательное, одушевлённое или неодушевлённое, род, число), общей системы изменения (например, глаголы спрягаются, существительные и прилагательные склоняются).
3. Одинакового набора словообразовательных и словоизменительных морфем (например, некоторые части речи имеют типичные суффиксы: – тель, – изн- – имена существительные).
4. Одинаковых синтаксических функций в составе предложения.
Применительно к нашей задаче, остановимся только на трёх частях речи: имени существительном, имени прилагательном и глаголе, так как для реализации морфологического разбора их будет вполне достаточно, а также данные части речи являются наиболее распространёнными. Также при описании данных частей речи более подробно разберём некоторые морфологические признаки, словообразовательные и словоизменительные морфемы, присущие для выбранных нами частей речи, причём более подробно следует обратить внимание на окончание, так как данный критерий в большей степени подходит нам для реализации задачи.
ИМЯ СУЩЕСТВИТЕЛЬНОЕ – это часть речи, отвечающая на вопросы кто? что?. К морфологическим признакам имени существительного относятся род, число, склонение и падеж существительного. Рассмотрим сначала род.
ИМЯ ПРИЛАГАТЕЛЬНОЕ – это часть речи, которая обозначает признак предмета и отвечает на вопросы: какой? какая? какое? какие? чей?. Прилагательные изменяются по родам, числам и падежам. Следовательно они всегда связанны с существительными и стоят в том же роде, числе и падеже, что и существительное, с которым они связанны. Следует также отметить, что прилагательные бывают:
– качественные (то есть выражают качество предмета)
– притяжательные (то есть выражают принадлежность придмета кому-либо)
– относительные (то есть указывает на отношение данного предмета к другим предметам).
ГЛАГОЛ – это часть речи, которая обозначает действие предмета и отвечает на вопросы: что делать? что сделать? Глагол имеет начальную форму – это инфинитив или неопределённая форма глагола.
Система является пакетом прикладных программ, предназначенного для морфологического разбора предложения с использованием алгоритма машины Тьюринга.
Объектами автоматизации являются процесс морфологического разбора. Создание данной системы показывает, что по принципу работы машины Тьюринга можно решать любые задачи на современных машинах, в различных программных средах.
Внедрение системы позволит обеспечить:
· Быстрый разбор предложения.
· Доступ к справочной информации системы.
Цели:
· составление диаграмм модели системы;
· составление диаграммы взаимодействия с целью распределения работ по анализу;
· составление алгоритма решения задачи на основании диаграмм активности и классов;
Сведения об использовании при проектировании нормативно-технических документов:
· ГОСТ 34.201–89 Виды, комплектность и обозначение документов при создании автоматизированных систем.
· ГОСТ 34.601–90 Автоматизированные системы, стадии создания.
· ГОСТ 34.602–89 Техническое задание на создание автоматизированной системы.
· РД 50–34.698–92 Виды испытаний автоматизированных систем.
· ГОСТ 19.105–78 ЕСПД Общие требования к программным продуктам
Описание процесса деятельности
Состав процедур или операций
Состав процедур или операций представлен на рисунке 7.

Рис. 7. Расширенная диаграмма прецедентов
Формирование требований к организации работ в условиях функционирования системы
- К использованию системы допускаются лица прошедшие обучение по работе с системой.
- Должна быть организованна поддержка конфиденциальности персональных данных для доступа к системе
Основные технические решения
Решения по структуре системы
На рисунке 8 изображена диаграмма классов, которая показывает множество классов, интерфейсов, коопераций и отношений между ними.

Рис. 8. Диаграмма классов
На данной диаграмме классов приведены классы, содержащие имена, атрибуты и операции, а также классы, содержащие только имена.
По данной диаграмме можно сделать следующие выводы о системе.
Во-первых, суть морфологии заключается в определении перечисленных частей речи, а также система морфологического разбора включает справочник. С помощью отношения обобщения показывается, что каждая из перечисленных частей речи является одной из множества себе подобных.
Во-вторых, отношение между морфологией и справочником показывает то что оба этих класса работают с одинаково большим массивом данных
На рисунке 9 изображена диаграмма компонентов, которая показывает на какие части будет разбита создаваемая система.

Рис. 9. Диаграмма компонентов
На диаграмме компонентов показаны программные модули и информационные модули.
Модуль Morfol_razbr.exe является управляющим, предназначенный для выполнения основных функций, то есть осуществление морфологического разбора текста введенного в данный модуль. При своей работе ониспользует остальные модули: Help.chm и BD.sql.
Решения по структуре информации
На рисунке 10 изображена логическая IDEF1X диаграмма, которая показывает и описывает все хранилища информации создаваемой системы и отношения между ними.

Рис. 10. Логическая IDEF1X диаграмма
Рабочий проект
На рисунке 11 изображена расширенная диаграмма классов.

Рис. 11. Расширенная диаграмма классов
На рисунке 12 изображена диаграмма активности.

Рис. 12. Диаграмма деятельности
На рисунках 13, 14, 15 изображён интерфейс программы
Рис. 13. Интерфейс программы. Выбор вида разбора
Рис. 14. Интерфейс программы. Ввод слова

Рис. 15. Интерфейс программы. Осуществление разбора
Текст программы:
#include «stdafx.h»
#include «17_Turing.h»
#include «17_TuringDlg.h»
#ifdef _DEBUG
#define new DEBUG_NEW
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
#endif
/////////////////////////////////////////////////////////////////////////////
// CAboutDlg dialog used for App About
class CAboutDlg: public CDialog
{
public:
CAboutDlg();
// Dialog Data
// {{AFX_DATA(CAboutDlg)
enum {IDD = IDD_ABOUTBOX};
// }} AFX_DATA
// ClassWizard generated virtual function overrides
// {{AFX_VIRTUAL(CAboutDlg)
protected:
virtual void DoDataExchange (CDataExchange* pDX); // DDX/DDV support
// }} AFX_VIRTUAL
// Implementation
protected:
// {{AFX_MSG(CAboutDlg)
// }} AFX_MSG
DECLARE_MESSAGE_MAP()
};
CAboutDlg:CAboutDlg(): CDialog (CAboutDlg:IDD)
{
// {{AFX_DATA_INIT(CAboutDlg)
// }} AFX_DATA_INIT
}
void CAboutDlg: DoDataExchange (CDataExchange* pDX)
{
CDialog: DoDataExchange(pDX);
// {{AFX_DATA_MAP(CAboutDlg)
// }} AFX_DATA_MAP
}
BEGIN_MESSAGE_MAP (CAboutDlg, CDialog)
// {{AFX_MSG_MAP(CAboutDlg)
// No message handlers
// }} AFX_MSG_MAP
END_MESSAGE_MAP()
/////////////////////////////////////////////////////////////////////////////
// CMy17_TuringDlg dialog
CMy17_TuringDlg:CMy17_TuringDlg (CWnd* pParent /*=NULL*/)
: CDialog (CMy17_TuringDlg:IDD, pParent)
{
// {{AFX_DATA_INIT (CMy17_TuringDlg)
m_text = _T(«»);
otvet = _T(«»);
q = 0;
// }} AFX_DATA_INIT
// Note that LoadIcon does not require a subsequent DestroyIcon in Win32
m_hIcon = AfxGetApp()->LoadIcon (IDR_MAINFRAME);
}
void CMy17_TuringDlg: DoDataExchange (CDataExchange* pDX)
{
CDialog: DoDataExchange(pDX);
// {{AFX_DATA_MAP (CMy17_TuringDlg)
DDX_Control (pDX, IDC_EDIT3, q1);
DDX_Control (pDX, IDC_RADIO1, mor);
DDX_Text (pDX, IDC_EDIT1, m_text);
DDX_Text (pDX, IDC_EDIT2, otvet);
DDX_Text (pDX, IDC_EDIT3, q);
// }} AFX_DATA_MAP
}
BEGIN_MESSAGE_MAP (CMy17_TuringDlg, CDialog)
// {{AFX_MSG_MAP (CMy17_TuringDlg)
ON_WM_SYSCOMMAND()
ON_WM_PAINT()
ON_WM_QUERYDRAGICON()
ON_BN_CLICKED (IDC_BUTTON1, OnButton1)
ON_BN_CLICKED (IDC_RADIO1, OnRadio1)
ON_BN_CLICKED (IDC_RADIO2, OnRadio2)
ON_BN_CLICKED (IDC_RADIO3, OnRadio3)
ON_BN_CLICKED (IDC_BUTTON3, OnFileClose)
//ON_BN_CLICKED (IDC_BUTTON4, OnButton4)
ON_BN_CLICKED (IDC_BUTTON2, OnButton2)
// }} AFX_MSG_MAP
END_MESSAGE_MAP()
/////////////////////////////////////////////////////////////////////////////
// CMy17_TuringDlg message handlers
BOOL CMy17_TuringDlg: OnInitDialog()
{
CDialog: OnInitDialog();
// Add «About…» menu item to system menu.
// IDM_ABOUTBOX must be in the system command range.
ASSERT((IDM_ABOUTBOX & 0xFFF0) == IDM_ABOUTBOX);
ASSERT (IDM_ABOUTBOX < 0xF000);
CMenu* pSysMenu = GetSystemMenu(FALSE);
if (pSysMenu!= NULL)
{
CString strAboutMenu;
strAboutMenu. LoadString (IDS_ABOUTBOX);
if (! strAboutMenu. IsEmpty())
{
pSysMenu->AppendMenu (MF_SEPARATOR);
pSysMenu->AppendMenu (MF_STRING, IDM_ABOUTBOX, strAboutMenu);
}
}
// Set the icon for this dialog. The framework does this automatically
// when the application's main window is not a dialog
SetIcon (m_hIcon, TRUE); // Set big icon
SetIcon (m_hIcon, FALSE); // Set small icon
// TODO: Add extra initialization here
return TRUE; // return TRUE unless you set the focus to a control
}
void CMy17_TuringDlg: OnSysCommand (UINT nID, LPARAM lParam)
{
if ((nID & 0xFFF0) == IDM_ABOUTBOX)
{
CAboutDlg dlgAbout;
dlgAbout. DoModal();
}
else
{
CDialog: OnSysCommand (nID, lParam);
}
}
// If you add a minimize button to your dialog, you will need the code below
// to draw the icon. For MFC applications using the document/view model,
// this is automatically done for you by the framework.
void CMy17_TuringDlg: OnPaint()
{
if (IsIconic())
{
CPaintDC dc(this); // device context for painting
SendMessage (WM_ICONERASEBKGND, (WPARAM) dc. GetSafeHdc(), 0);
// Center icon in client rectangle
int cxIcon = GetSystemMetrics (SM_CXICON);
int cyIcon = GetSystemMetrics (SM_CYICON);
CRect rect;
GetClientRect(&rect);
int x = (rect. Width() – cxIcon + 1) / 2;
int y = (rect. Height() – cyIcon + 1) / 2;
// Draw the icon
dc. DrawIcon (x, y, m_hIcon);
}
else
{
CDialog: OnPaint();
}
}
// The system calls this to obtain the cursor to display while the user drags
// the minimized window.
HCURSOR CMy17_TuringDlg: OnQueryDragIcon()
{
return (HCURSOR) m_hIcon;
}
void CMy17_TuringDlg: OnButton1 ()
{
// TODO: Add your control notification handler code here
UpdateData(true);
int i = strlen (m_text);
char x1 = m_text [i-1];
char x2 = m_text [i-2];
char x3 = m_text [i-3];
{if ((x1 == «й' && (x2 == 'ы» || x2 == «и' || x2 == 'о» || x2 == 'а'))
|| (x1 == «ю' && (x2 =='у» || x2 == 'ю'))
|| (x1 =='е' && (x2 == «и' || x2 =='о» || x2 == 'е' || x2 == 'ы'))
|| (x3 == «о' && ((x2 == 'г» && x1 == «о') || (x2 == 'м» && x1 == 'у'))
|| (x1 == 'м' && x2 == 'ы') ||
(x3 == «е' && x2 =='г» && x1 == 'о')))
{
otvet = «прилагательное»;
}
else
{
if (((x2 == «т' && (x1 == 'ь» || x1 == «и')) || (x1 == 'я» && x2 == 'с'))
|| (x1 == «ь' && x2 == 'т» && (x3 == «а' || x3 == 'е» ||x3 == 'и'))
|| (x1 == «т' && (x2 == 'е» || x2 == «и' || x2 == 'у» || x2 == «ю' || x2 == 'а» || x2 == 'я'))
|| (x1 == «е' && x2 == 'т» && (x3 == 'е' || x3 == 'и'))
|| (x1 == «ь' && x2 == 'ш» && (x3 == 'е' || x3 == 'и'))
|| (x1 == «м' && (x2 == 'и» || x2 == 'и'))
|| x1 == 'У')
{
otvet = «глагол»;
}
else
{
if ((x1=='а'||x1=='я'||x1=='о'||x1=='е'|| x1 == «з' ||x1=='и'||x1=='ы'||x1=='у» || x1 == «ь'|| x1 == 'с» || x1 == «ф' || x1 == 'ы» || x1 == «т' || x1 == 'р» || x1 == 'к')
|| (x2 == «и' && (x1 == 'я» || x1 == 'м' || x1 == 'е'))
|| (x2 == «ь' && (x1 == 'е» || x1 == 'и'))
|| (x2 == «о' && (x1 == 'й» || x1 == 'е'))
|| (x1 == 'а' && x2 == 'я')
|| (x1 == «ь' && x2 == 'т» && x3 == 'с')
|| (x1 == «я' || x2 == 'с» || x3 == 'й'))
{
otvet = «существительное»;
}
else
{
otvet = «yне удаётся распознать»;
}
}
}
UpdateData(false);
}
}
void CMy17_TuringDlg: OnRadio1 ()
{
// TODO: Add your control notification handler code here
q1. EnableWindow(false);
}
void CMy17_TuringDlg: OnRadio2 ()
{
// TODO: Add your control notification handler code here
q1. EnableWindow(true);
}
void CMy17_TuringDlg: OnRadio3 ()
{
// TODO: Add your control notification handler code here
q1. EnableWindow(true);
}
void CMy17_TuringDlg: OnFileClose()
{
// TODO: Add your control notification handler code here
}
void CMy17_TuringDlg: OnButton4 ()
{
// TODO: Add your control notification handler code here
}
void CMy17_TuringDlg: OnButton2 ()
{
otvet = «»;
m_text = «»;
UpdateData(false);
// TODO: Add your control notification handler code here
}
Список литературы
1. Катленд Н. Вычислимость. Введение в теорию рекурсивных функций: Пер. с англ. М.: Мир, 1983.
2. Холзнер С. Visual C++ 6. Учебный курс. СПб.: Питер, 2007.
3. https://ru.wikipedia.org
4. https://www.intuit.ru
5. https://www.metric.ru
6. https://old.osp.ru