найти:
1. Нормированные волновые функции частицы
2. Возможные значения энергии частицы
3. Для основного состояния частицы наиболее вероятное значение расстояния r вер, а также вероятность нахождения частицы в области r < r вер
Решение
Задания 1 и 2
Возможные значения энергии частицы находим, решая операторное уравнение
Поскольку потенциал имеет сферическую симметрию, то оператор Лапласа разумно будет записать также в сферических координатах
Кроме того, волновая функция частицы в потенциале, который зависит только от одной координаты r, будет также зависеть только от этой одной координа-ты. Тогда дифференцирование волновой функции по остальным переменным будет давать нуль, а значит, в выражении для оператора Лапласа можно оста-вить только те слагаемые, которые содержат производные только по r
Следуя форме потенциала, разделим пространство на две области – первая область внутри сферы радиуса R0, а вторая - за пределами этой сферы. Для каждой из этих областей составим и решим уравнение Шредингера, а потом «сошьем» решения на границе областей. Итак, уравнения
в чем-то похожи на те, что мы детально исследовали в разделе 1. Второе уравнение содержит бесконечно большое слагаемое, поэтому его решение – волновая функция, тождественно равная нулю.
Первое уравнение отличается от того, что мы анализировали в разделе 1, тем, что содержит в операторе Лапласа дополнительное слагаемое. Такое уравнение решается стандартным методом подстановки
,
где функция c(r) является неизвестной. После подстановки волновой функции в таком виде в уравнение Шредингера, выполнения всех необходимых операций дифференцирования и всех возможных сокращений приходим к уравнению для c(r)
которое является хорошо изученным и до боли знакомым уравнением гармонических колебаний. Его решение
Возвращаемся к подстановке (). Тогда волновая функция принимает вид
Для нахождения констант интегрирования А и В воспользуемся следующими соображениями. Вследствие деления на r, в волновой функции в точке r =0 имеется сингулярность, или, проще говоря, возрастание к бесконечно большой величине. Волновая функция, однако, не имеет права быть неограниченной, поэтому, чтобы избавиться от этой неприятности нам остается только потребовать, чтобы числитель также стремился к нулю. Тогда неопределенность типа 
легко раскрывается (хотябы по правилу Лопиталя) и приводит к конечной величине y(r). Тогда условие
дает В =0 и волновая функция принимает вид
Далее воспользуемся граничным условием. Волновая функция на границе областей должна совпадать. Так как в области r >R0 она равна нулю, то и на границе (то есть в точках с r =R0) тоже должна принимать нулевое значение
Автоматически это дает
Таким образом, энергетический спектр частицы нами уже получен.
Последнюю неизвестную константу интегрирования А находим из условия нормировки, которое состоит в том, что волновая функция, после интегрирования в квадрате по объему dV=4 p r 2 d r должна дать единицу
тогда 
, и искомое выражение для волновой функции приобретает вид
Задание 3.
Для нахождения наиболее вероятного значения r вер необходимо исследовать на предмет наличия экстремума функцию 
, которая является плотностью вероятности нахождения частицы в сферическом слое толщины dr. Дифференцирование 
по r дает нам условие экстремума
или, с учетом соотношения (), а также того, что, по условию, частица находится в основном энергетическом состоянии (т.е. n =1), определяем значения rextr, соответствующие экстремумам функции 
:
1. 
rextr1 = 0, rextr2 = R0
соответствуют минимумам функции , в чем легко убедиться прямой подстановкой.
2. 
rextr3 = R0/2 = r вер соответствует максимуму функции плотности вероятности и как раз является искомым наиболее вероятным значением.
Поиск вероятности нахождения частицы в области r < r вер сводится к вычислению интеграла
 |
Рис.3
На рис.3 представлена зависимость для R0=1, откуда очевидно, что максимум приходится на точку r вер = 1 / 2.
Туннельный эффект
Явление туннелирования относится к группе самых ярких явлений, экспериментально подтверждающих теоретические положения квантовой механики. На бытовом уровне невозможно понять, как частица умудряется пробраться через некоторое пространство, если ее энергии для этого недостаточно? Яркий пример тому – естесственная радиоактивность ядер: взаимодействие между нуклонами в ядре настолько велико, что непонятно, по какой причине время от времени из ядер, скажем, стронция вылетают альфа-частицы. Следует сразу подчеркнуть, что вооружившись всеми теми знаниями, которые дает квантовая механика, мы все равно этого не узнаем, ибо вопрос «почему?» - это вопрос не по адресу. Квантовая механика в состоянии ответить только на вопрос «какова вероятность того, что данное событие при определенных условиях будет иметь место », не вникая в причины этого явления.
Таким образом, вопрос, а какова вероятность прохождения частицы через данную область пространства, для которой известен аналитический вид потенциала, является правомочным и ответ на него мы получим, вычислив коэффициент туннелирования.
Постановка задачи
Найти для электрона, имеющего энергию Е, вероятность D прохождения потенциального барьера шириной l и высотой U 0, если барьер имеет форму как на графиках, представленных на рис.4 а), б), в). Уточнение: на графике в) представлена квадратичная парабола. Для этого
1. Написать аналитическое выражение для потенциалов U(x) в области 0£x£ l.
2. Для каждого варианта определить координаты x1, x2, соответствующие координатам точек входа и выхода из барьера соответственно.
3. Вычислить коэффициент прохождения, воспользовавшись формулой
| |||||||
|
| ||||||
 | |||||||
|
 |  |  |
|
|
|
|
Рис.4
Решение
Задания будем выполнять параллельно для всех трех вариантов.
Задание 1
а) Очевидно, 
б) Как видно из графика, потенциал линейно зависит от координаты
в) Согласно условию, потенциал квадратично зависит от координаты. Поскольку «рожки» параболы направлены вниз, коэффициент при старшей степени x отрицаиелен, а всилу симметричного расположения параболы относительно оси ординат, коэффициент при линейном члене равен нулю. Воспользовавшись тем фактом, что парабола проходит через точки (0, U 0) и (± l /2, 0), находим аналитический вид потенциала
Задание 2
Точки x 1 и x 2 это точки пересечения графика U(x) и прямой U=Е
а) Этот случай тривиальный, поэтому сразу запишем
б) Координату входа в барьер находим из уравнения 
, а координату выхода – по графику
в) Симметричные относительно оси ординат точки входа-выхода из барьера находим из уравнения 
их значения 
Задание 3
а) 
б) 
в)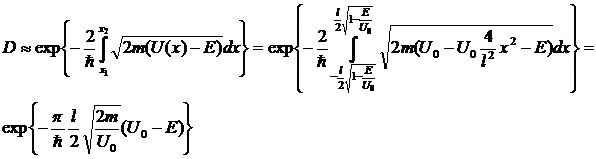 
Примечание: взятие последнего интеграла производится при помощи стандартной тригонометрической замены
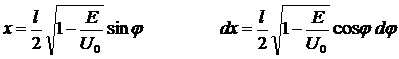
С целью проверки полученных знаний и навыков студентам предлагается приведенная ниже самостоятельная работа