Примеры применения формул понижения степени

Формулы понижения степени в тригонометрии.

Одним из видов тригонометрических формул являются формулы понижения степени. Формулы понижения степени выражают степени синуса и косинуса через синус и косинус первой степени, но кратного угла. Таким образом, эти формулы понижают степень исходных тригонометрических функций с n-ой до первой, но при этом повышают кратность угла от до 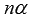. В этой статье мы выведем формулы понижения степени для степеней со второй по четвертую, дадим общий вид формул понижения для n-ой степени, а также рассмотрим примеры их применения.

Формулы понижения степени, их доказательство

Запишем формулы понижения степени со второй по четвертую для синуса и косинуса, ниже приведем их вывод. А после этого дадим общий вид формул понижения степени.

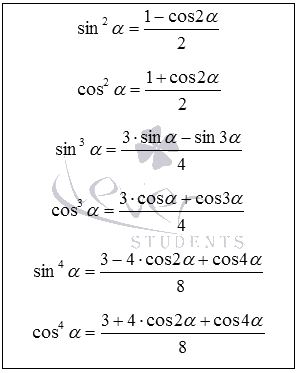
Теперь перейдем к выводу этих формул понижения степени.

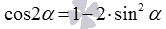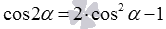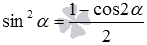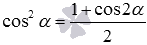Формулы понижения для квадрата синуса и косинуса напрямую следуют из формул двойного угла вида и . Записанные равенства достаточно лишь разрешить относительно синуса в квадрате и косинуса в квадрате, что даст формулы и соответственно.

Здесь стоит отметить, что формулы понижения степени для синуса и косинуса в квадрате совпадают с формулами синуса и косинуса половинного угла.

Двигаемся дальше.

Если формулы тройного угла вида 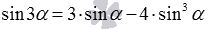и 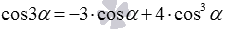разрешить относительно синуса в кубе и косинуса в кубе, то получатся формулы понижения степен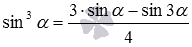и и 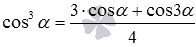соответственно.

Доказать формулы понижения с четвертой степени вида 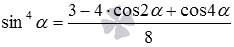и 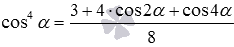можно, дважды обратившись к формулам понижения синуса и косинуса в квадрате:

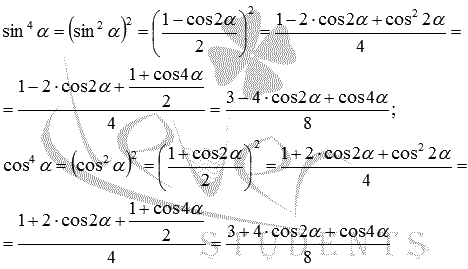
Пришло время записать общий вид формул понижения степени. Для четных показателей степени (то есть, для n=2, 4, 6, …) они имеют вид 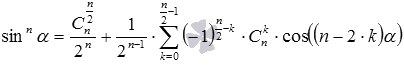и ,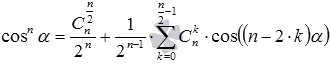
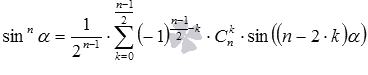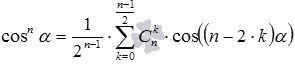а для нечетных (то есть, для n=3, 5, 7, …) - вид и , где 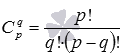- число сочетаний из p элементов по q.

Покажем, как использовать формулы понижения степени общего вида на конкретном примере. Запишем с их помощью формулу понижения степени для синуса в кубе. Так как показатель степени 3 является нечетным числом, то нужно воспользоваться формулой 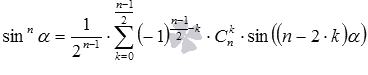, приняв n=3. Для n=3 имеем

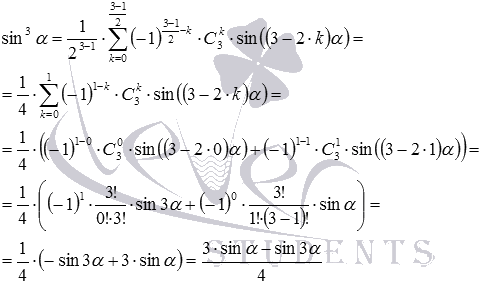
К началу страницы

Примеры применения формул понижения степени

Разберем решения нескольких простых примеров, в которых используются формулы понижения степени. Это мы сделаем для того, чтобы стало понятно, как применяются эти формулы.

Пример.

Проверьте справедливость формулы понижения степени вида 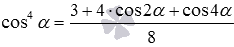, взяв .

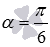Решение.

Чтобы проверить справедливость указанной формулы понижения степени для данного значения угла , нужно вычислить значения левой и правой частей и убедиться, что они равны.

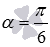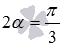Так как , то и 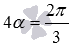. Известно, что 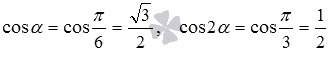и 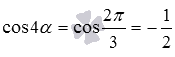(при необходимости смотрите статью значения синуса, косинуса, тангенса и котангенса, тогда 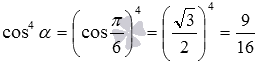и.

Таким образом, значения левой и правой частей формулы понижения степени вида 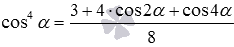совпадают при 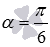, что подтверждает справедливость этой формулы для данного угла.

Формулы понижения степени можно применять и для углов, вид которых отличен от . Следующий пример служит иллюстрацией этой мысли.

Пример.

Воспользуйтесь формулой понижения степени для .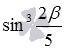

Решение.

Соответствующая формула понижения степени для угла имеет вид .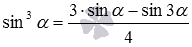

Используем формулу понижения для угла 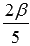, для чего выполним замену на 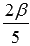. При этом получим 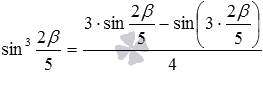, что эквивалентно равенству .

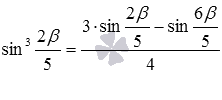Ответ:

.

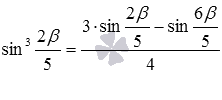В заключение отметим, что формулы понижения степени наиболее часто приходится использовать для преобразования тригонометрических выражений, но об этом будет отдельный разговор.